phitheta2uv
Convert phi/theta angles to u/v coordinates
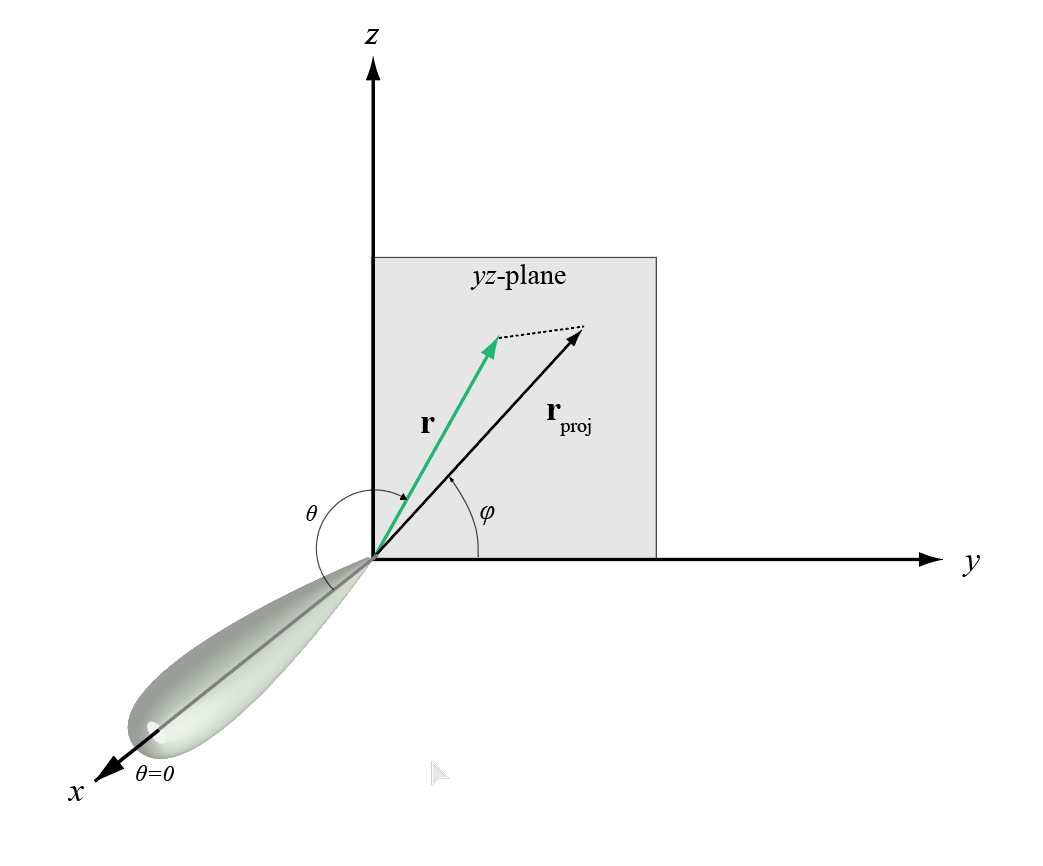
Description
UV = phitheta2uv(PhiTheta)
Examples
Input Arguments
Output Arguments
More About
Extended Capabilities
Version History
Introduced in R2012a