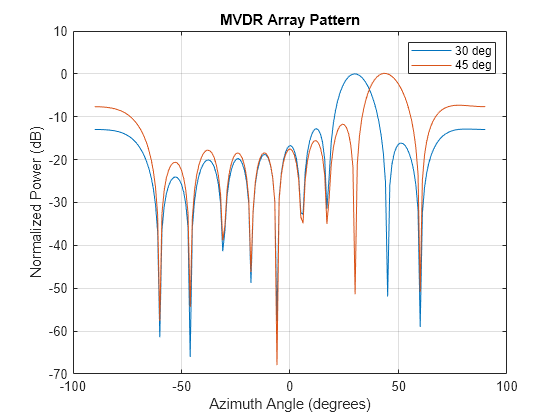
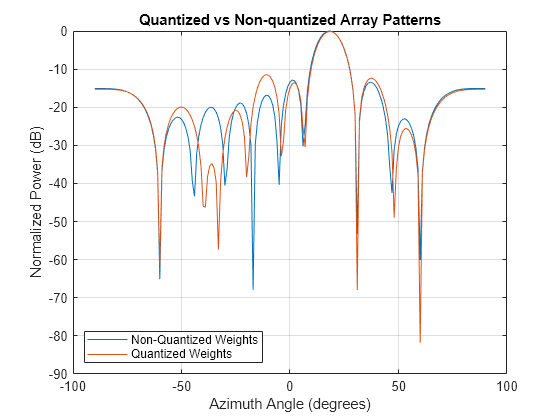
mvdrweights
Minimum variance distortionless response (MVDR) beamformer weights
Description
wt = mvdrweights(pos,ang,cov)pos argument
specifies the sensor positions of the array. The ang argument
specifies the azimuth and elevation angles of the desired response
directions. cov is the sensor spatial covariance
matrix between sensor elements. The output argument, wt,
is a matrix contains the beamformer weights for each sensor and each
direction. Each column of wt contains the weights
for the corresponding direction specified in ang.
All elements in the sensor array are assumed to be isotropic.
Examples
Input Arguments
Output Arguments
More About
References
[1] Van Trees, H.L. Optimum Array Processing. New York, NY: Wiley-Interscience, 2002.
[2] Johnson, Don H. and D. Dudgeon. Array Signal Processing. Englewood Cliffs, NJ: Prentice Hall, 1993.
[3] Van Veen, B.D. and K. M. Buckley. “Beamforming: A versatile approach to spatial filtering”. IEEE ASSP Magazine, Vol. 5 No. 2 pp. 4–24.
Extended Capabilities
Version History
Introduced in R2013a
See Also
steervec | cbfweights | lcmvweights | sensorcov | phased.MVDRBeamformer