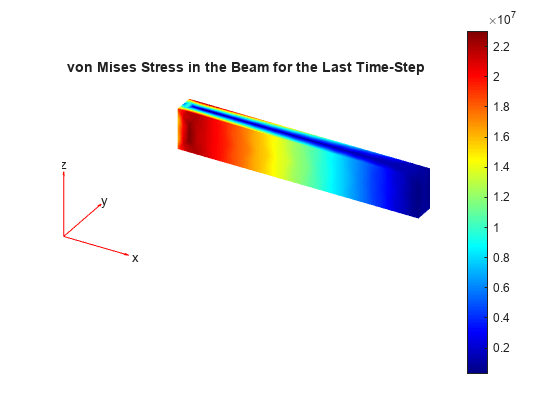
evaluateVonMisesStress
Evaluate von Mises stress for dynamic structural analysis problem
Description
vmStress = evaluateVonMisesStress(structuralresults)
Examples
Input Arguments
Output Arguments
Version History
Introduced in R2018a