Pulsating High Freq Observer

Estimate initial rotor electrical position of interior PMSM using pulsating high frequency (PHF) injection

Since R2022b

• 

Libraries:
Motor Control Blockset / Sensorless Estimators

Description

The Pulsating High Frequency Observer block estimates the initial position (in electrical radians) of a stationary interior PMSM by using pulsating high-frequency (PHF) injection and dual-pulse (DP) techniques. In addition, the block also detects the real-time position when the rotor runs using (low-speed) closed-loop control.

For more information about the block algorithm, see Algorithm.

Examples

Estimate Initial Rotor Position Using Pulsating High-Frequency and Dual-Pulse Methods

Estimates the initial position (in electrical radians) of a stationary interior PMSM by using pulsating high-frequency (PHF) injection and dual pulse (DP) techniques.

Open Model

Ports

Input

I_{ab hf} — PHF current response

vector

The high-frequency (phase a and b) current feedback from the motor in response to the PHF voltage injection, in amperes or per-unit.

Data Types: single | double | fixed point

Enable — Input to trigger block operation

scalar

Specify one of these inputs at this port:

• 1 — Enable block operation

• 0 — Disable block operation

Data Types: Boolean

θ_in — Initial rotor position

scalar

Initial rotor position input when the block skips the stage 1 initial position estimation (IPE) operation. The position is expressed in radians, degrees, or per-unit. For more information on the two stages that the block operates in, see Algorithm.

The unit depends on the Position unit parameter.

Data Types: single | double | fixed point

IPE_En — Enable stage 1 initial position estimation (IPE) operation

scalar

Port for signal to enable stage 1 IPE operation. It supports one of the following inputs:

• 1 — Enable the block to run the stage 1 IPE operation followed by the stage 2 closed-loop pulsating high-frequency (PHF) injection operation.

• 0 — Enable the block to skip stage 1 and directly run stage 2 closed-loop PHF injection.

For more information on the two stages that the block operates in, see Algorithm.

Data Types: Boolean

Output

V_{αβ hf} — PHF output

scalar

Pulsating high-frequency voltage (in αβ reference frame) output, in per-unit.

Data Types: single | double | fixed point

θ_est — Estimated rotor position

scalar

The rotor position estimated by the block, in radians, degrees, or per-unit.

The unit depends on the Position unit parameter.

Data Types: single | double | fixed point

Pos_En — Status of θ_est port

scalar

The port provides one of the following outputs:

• 1 — Indicates that the block has successfully completed the stage 1 initial position estimation (IPE) and that the θ_est port displays the accurate rotor position.

• 0 — Indicates that the stage 1 IPE operation is still in progress (θ_est port output is not accurate as yet) or that the estimation has failed.

Data Types: single | double | fixed point

Info — Bus signal

bus

The bus signal contains these block calculations.

Signal				Description	Units
Sin θest and cos θest				Sine and cosine of estimated rotor position	-
Id and Iq				Stator direct axis and quadrature axis currents	A
Convergence				Difference between current and previous sample of θest output. A value closer to zero indicates saturation of θest.	rad
Status			0	Block is not enabled (Enable input port is 0)	-
			1	Block is finding the best possible initial estimate (stage 1 part A)	-
			2	Block is running the PHF method (stage 1 part B)	-
			3	Block is running the DP method (stage 1 part C)	-
			4	Block has successfully completed stage 1 and has started stage 2 closed-loop PHF injection	-
			5	Stage 1 part B failed due to a large error in the estimated rotor position	-

Parameters

Discrete step size (s) — Sample time after which block executes again

50e-6 (default) | scalar

The time between two consecutive instances of block execution.

Input units — Unit of block inputs

Per-unit (default) | SI

Units of measure for the block inputs.

Datatype — Input and output data type

single (default) | double | fixed point

Data type of the block inputs and outputs.

Compute PHF parameters automatically using motor parameters — Automatically compute PHF parameters

off (default) | on

Selecting this parameter enables the block to automatically compute the following PHF parameters (available on the PHF Parameters tab) using the specified motor parameters:

• PHF frequency (Hz)

• LP filter cutoff frequency (Hz)

• Proportional gain

• Integral gain

• Expected settling time (s)

• Expected damping ratio

• Open loop duration (s)

• Close loop duration (s)

• Idle time (s)

For more information about how the block computes these PHF parameters, see Compute PHF Parameters.

If you select this parameter, the block disables the Compute PHF parameters button.

Compute DP parameters automatically using motor parameters — Automatically compute DP parameters

off (default) | on

Selecting this parameter enables the block to automatically compute the DP parameter Pulse duration (s) (available on the DP Parameters tab) using the specified motor parameters.

For more information about how the block computes the DP parameter, see Compute DP Parameters.

If you select this parameter, the block disables the Compute DP parameters button.

Motor Parameters

Stator resistance (ohm) — Motor resistance

0.1458 (default) | scalar

Resistance of the stator (in ohms).

Stator d-axis inductance (H) — Motor inductance

0.00013016 (default) | scalar

Inductance of the stator along the d-axis of the d-q reference frame.

Stator q-axis inductance (H) — Motor inductance

0.00014098 (default) | scalar

Inductance of the stator along the q-axis of the d-q reference frame.

Base voltage (V) — Rated voltage

13.8564 (default) | scalar

Rated voltage of the motor (in volts).

Base current (A) — Rated current

21.4286 (default) | scalar

Rated current of the motor (in amperes).

Compute PHF parameters — Compute PHF parameters manually

button

When you click this button, the block computes the following PHF parameters (available on the PHF Parameters tab) manually using the specified motor parameters:

• PHF frequency (Hz)

• LP filter cutoff frequency (Hz)

• Proportional gain

• Integral gain

• Expected settling time (s)

• Expected damping ratio

• Open loop duration (s)

• Close loop duration (s)

• Idle time (s)

For more information about how the block computes these PHF parameters, see Compute PHF Parameters.

Dependencies

To enable this parameter, clear the Compute PHF parameters automatically using motor parameters parameter.

Compute DP parameters — Compute DP parameters manually

button

When you click this button, the block computes the DP parameter Pulse duration (s) (available on the PHF Parameters tab) manually using the specified motor parameters:

For more information about how the block computes the DP parameter, see Compute DP Parameters.

Dependencies

To enable this parameter, clear the Compute DP parameters automatically using motor parameters parameter.

PHF Parameters

PHF peak voltage (PU) — Peak voltage of PHF

0.2 (default) | scalar

Peak amplitude of the PHF voltage applied by the block, in volts.

PHF frequency (Hz) — PHF voltage frequency

2000 (default) | scalar

Frequency of the PHF voltage applied by the block, in Hz.

LP filter cutoff frequency (Hz) — Cutoff frequency for lowpass filter of PHF

131.9037 (default) | scalar

Cutoff frequency of the lowpass filter for the PHF applied by the block, in Hz.

Select tuning parameters — Select control parameters for manual tuning

Controller gains (default) | Time response variables

Select the control parameters that you want to manually tune.

• Controller gains — Select this option to enable these control parameters:

  • Proportional gain

  • Integral gain

  Note

  Selecting Control gains disables the time response variables.

• Time response variables — Select this option to enable these control parameters:

  • Expected settling time (s)

  • Expected damping ratio

  Note

  Selecting Time response variables disables the control gains variables.

To see the effects of the tuned parameters on the disabled control parameters, you can click the Compute Control Parameters button. For more details, see Compute Control Parameters.

Proportional gain — Proportional gain for PI controller of PHF

1954.6647 (default) | scalar

Proportional PI controller gain, K_p, for the PHF applied by the block.

Dependencies

To enable this parameter, set the Select tuning parameters parameter to Controller gains.

Integral gain — Integral gain for PI controller of PHF

7392.5303 (default) | scalar

Integral PI controller gain, K_i, for the PHF applied by the block.

Dependencies

To enable this parameter, set the Select tuning parameters parameter to Controller gains.

Expected settling time (s) — Expected settling time of estimated position

0.66794 (default) | scalar

The expected time for the block output θ_est to saturate during part B.

Dependencies

To enable this parameter, set the Select tuning parameters parameter to Time response variables.

Expected damping ratio — Expected damping ratio of block output θ_est

0.99 (default) | scalar

The expected damping ratio of the block output θ_est dynamics.

Dependencies

To enable this parameter, set the Select tuning parameters parameter to Time response variables.

Compute Control Parameters — Compute disabled control parameters

button

Compute the control parameters that are disabled in the Control Parameters section. This parameter helps you update the disabled control parameters according to the edits you made to the enabled control parameters. This table describes the equations that the block uses to compute the disabled control parameters.

Control Parameter	Expression or Value	Remarks
Proportional gain, kp	$$\frac{\ln \left(20000\right)}{G\cdot T_{settling}}$$	The Compute Control Parameters button computes these values when you enable the time response variables for manual edits.
Integral gain, ki	$$\frac{G{\left(k_p\right)}^2}{4{\delta }^2}$$
Expected settling time (s), Tsettling	$$\begin{array}{l}\frac{\ln \left(20000\right)}{G\cdot k_p},\text{when }\delta \le 1\\ \frac{\ln \left(20000\right)}{G\cdot k_p}\left(\frac{2\delta }{\left(\delta -\sqrt{{\delta }^2-1}\right)}\right),\text{when }\delta >1\end{array}$$	The Compute Control Parameters button computes these values when you enable the controller gains for manual edits.
Expected damping ratio, ẟ	$$\frac{k_p}{2}\sqrt{\frac{G}{k_i}}$$

In the expressions:

• $$G=\frac{V_{phf}\left(L_q-L_d\right)}{4\pi f_h{L}_d{L}_q}$$

• V_phf is the peak amplitude value of the injected high frequency voltage signal (in volts).

• L_d and L_q are the d and q axis stator inductances (in henry).

• f_h is the frequency of the injected high-frequency voltage.

Note

The expressions in this table use elements and values based on the reference papers as well as experimental data.

Open loop duration (s) — Duration of open-loop PHF injection during stage 1 part A

0.0066794 (default) | scalar

Duration of the open-loop PHF injection during stage 1 part A, in seconds.

Close loop duration (s) — Duration of closed-loop PHF injection during stage 1 part B

0.66794 (default) | scalar

Duration of the closed-loop PHF injection during stage 1 part B, in seconds.

Idle time (s) — Duration between algorithm steps

0.0066794 (default) | scalar

Duration (in seconds) between steps in the algorithm related to stage 1 part A and stage 1 part B that allow for fading of transient dynamics. For example, this block stops operating (for this duration) between each PHF injection (open loop or closed loop).

Error threshold (rad) — Minimum error threshold for θ_err

4e-4 (default) | scalar

The minimum error value θ_err at which the convergence of estimated rotor position θ_est completes.

DP Parameters

Pulse voltage (PU) — Amplitude of injected pulses

0.5 (default) | scalar

Voltage amplitude of the injected pulses, in volts.

Pulse duration (s) — Duration of injected pulses

0.00066955 (default) | scalar

Duration of the injected pulses, in seconds.

Idle time (s) — Duration between two pulses during dual-pulse injection

50e-3 (default) | scalar

Duration (in seconds) between two pulses during the dual-pulse injection (stage 1 part C).

Algorithms

The block determines the best possible initial estimation for the rotor position using open-loop pulsating high-frequency (PHF) injection, which it uses to run closed-loop PHF.

The block executes closed-loop PHF by injecting a high-frequency signal into the estimated rotor position to determine the actual rotor position without spinning the motor. This technique works when the motor saliency ratio (L_q/L_d) is greater than 1. Due to a limitation in the PHF method, the estimated position can show ambiguity equal to the value of π (pi). The dual-pulse (DP) method uses polarity detection to resolve the ambiguity of π and applies a compensation of π if there is an error. The estimated rotor position ranges from 0 to 2π electrical radians.

The block can run in these two stages:

1. Stage 1 – Initial position estimation (IPE), which includes three parts.

2. Stage 2 – Closed-loop pulsating high-frequency (PHF) injection.

After Stage 1 completes, you can continue to run the block in Stage 2 where it computes the rotor position while the motor runs using closed loop control (for example, field-oriented control or FOC). Using the Stage 2 algorithm (closed-loop PHF injection), the block can continue to inject pulsating high frequency (as described in Part B) and use the numerical analysis of the resulting stator current response to compute and track the rotor position during closed-loop operation.

Stage 1 focuses on determining the initial position of the rotor when it is stationary. This stage includes the following three parts.

Part A: Find Best Possible Initial Estimation

The block uses the PHF injection technique. PHF injection needs initial estimation to start the algorithm.

If you use only one initial estimation, θ_{i_est}, (for PHF) for all possible actual rotor positions, the block algorithm might not work accurately for certain actual rotor positions when the motor has low saliency. These ambiguous positions are:

1. When θ_actual lies in the range $$\left[\left({\theta }_{i\_est}+ \frac{\pi }{2}-0.1\right),\left({\theta }_{i\_est}+ \frac{\pi }{2}+0.1\right)\right]$$

2. When θ_actual lies in the range $$\left[\left({\theta }_{i\_est}- \frac{\pi }{2}-0.1\right),\left({\theta }_{i\_est}- \frac{\pi }{2}+0.1\right)\right]$$

3. When θ_actual lies in the range $$\left[\left({\theta }_{i\_est}+\pi -0.1\right),\left({\theta }_{i\_est}+ \pi +0.1\right)\right]$$

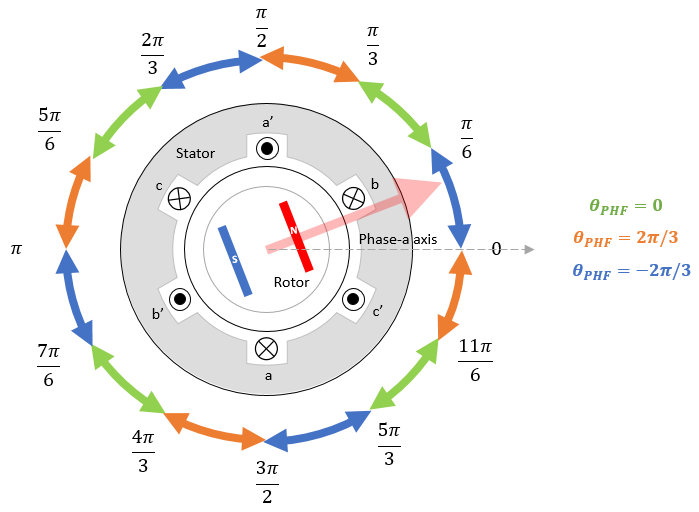
To make PHF work for motors with low saliency, the block picks different initial estimation for different actual rotor positions.

The block picks the best possible initial estimation from these three alternatives:

1. θ_{i_est} = 0

2. θ_{i_est} = 2π/3

3. θ_{i_est} = -2π/3

Therefore, the block sequentially injects three high-frequency voltage signals (that have the same peak amplitude V_phf and the same frequency f_h) across the preceding 3 θ_{i_est} values and measures the resulting i_q currents.

Note

In Part A, each high frequency voltage signal injection happens for a fixed time duration (Open loop duration (s) parameter). In addition, two consecutive injections have a fixed delay between them (Idle time (s) parameter).

The following equations describe the injected voltages in the estimated d-q reference frame:

$$\begin{array}{l}{v}_{d\_est}=V_{phf}\sin (2\pi f_{h}t)\\ v_{q\_est}=0\end{array}$$

The following equations describe the injected voltages in the estimated α-β reference fame:

$$\begin{array}{l}{v}_{\alpha }=V_{phf}\cos ({\theta }_{i\_est})\sin (2\pi f_{h}t)\\ v_{\beta }=V_{phf}\sin ({\theta }_{i\_est})\sin (2\pi f_{h}t)\end{array}$$

The following equations describe the injected voltages in the actual d-q reference frame:

$$\begin{array}{l}{v}_d=V_{phf}\cos ({\theta }_{err})\sin (2\pi f_{h}t)\\ v_q=-V_{phf}\sin ({\theta }_{err})\sin (2\pi f_{h}t)\end{array}$$

We can derive the following equation for the resulting i_q current using the IPMSM motor dynamic equations:

$$i_q=\frac{V_{phf}\left(L_d-L_q\right)\sin (2{\theta }_{err})}{4\pi f_h{L}_d{L}_q}\cos \left(2\pi f_{h}t\right)$$

$$i_{q\_peak}\propto \left|\sin \left(2{\theta }_{err}\right)\right|$$

Therefore, $i_{q\_peak}\propto \left|sin\left(2({\theta }_{actual}-{\theta }_{i\_est})\right)\right|$

, where

θ_{i_est} — Initial estimation of rotor position (which can be either 0, 2π/3, or -2π/3) (in degrees, per-unit, or radians).

θ_actual — Actual rotor position (in degrees, per-unit, or radians)

θ_err = θ_actual-θ_{i_est} (in degrees, per-unit, or radians).

L_d and L_q are the d and q axis inductances of the IPMSM.

V_{d_est} and V_{q_est} are the voltages injected across the d and q axes of the estimated d-q reference frame.

V_d and V_q are the voltages injected across the d and q axes of the actual d-q reference frame.

V_α and V_β are the voltages injected across the α and β axes of the stationary α-β reference frame.

With

i_q1 = i_{q_peak} for θ_{i_est} = 0

i_q2 = i_{q_peak} for θ_{i_est} = 2π/3

i_q3 = i_{q_peak} for θ_{i_est} = -2π/3

For θ_{i_est} = 0, when you vary θ_actual from 0 to 2π, $i_{q1}\propto \left|sin 2({\theta }_{actual}-0)\right|$ is the maximum value between the i_q1, i_q2, and i_q3 current peak values when the rotor lies in the following four highlighted regions.

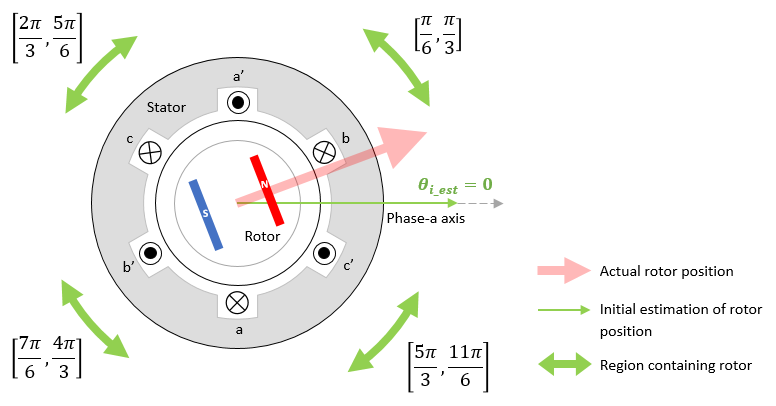
If θ_{i_est} = 0 is used for all θ_actual = 0 to 2π, the algorithm fails for following ambiguous regions (when motor saliency is low):

1. θ_actual lies in the range $$\left[\left(0+ \frac{\pi }{2}-0.1\right),\left(0+ \frac{\pi }{2}+0.1\right)\right]$$

2. θ_actual lies in the range $$\left[\left(0- \frac{\pi }{2}-0.1\right),\left(0- \frac{\pi }{2}+0.1\right)\right]$$

3. θ_actual lies in the range $$\left[\left(0+\pi -0.1\right),\left(0+ \pi +0.1\right)\right]$$

Because these ambiguous regions are not present in the preceding four regions, you can eliminate the regions where the algorithm might fail.

For θ_{i_est} = (2π/3), when you vary θ_actual from 0 to 2π, $i_{q2}\propto \left|sin 2({\theta }_{actual}-\frac{2\pi }{3})\right|$ is the maximum value between the i_q1, i_q2, and i_q3 current peak values when the rotor lies in the following four highlighted regions.

If θ_{i_est} = (2π/3) is used for all θ_actual = 0 to 2π, the algorithm fails for following ambiguous regions (when motor saliency is low):

1. θ_actual lies in the range $$\left[\left(\frac{2\pi }{3}+ \frac{\pi }{2}-0.1\right),\left(\frac{2\pi }{3}+ \frac{\pi }{2}+0.1\right)\right]$$

2. θ_actual lies in the range $$\left[\left(\frac{2\pi }{3}- \frac{\pi }{2}-0.1\right),\left(\frac{2\pi }{3}- \frac{\pi }{2}+0.1\right)\right]$$

3. θ_actual lies in the range $$\left[\left(\frac{2\pi }{3}+\pi -0.1\right),\left(\frac{2\pi }{3}+ \pi +0.1\right)\right]$$

Because these ambiguous regions are not present in the preceding four regions, you can eliminate the regions where the algorithm might fail.

For θ_{i_est} = -(2π/3), when you vary θ_actual from 0 to 2π, $i_{q3}\propto \left|sin 2({\theta }_{actual}-\left(-\frac{2\pi }{3}\right))\right|$ is the maximum value between i_q1, i_q2, and i_q3 current peak values when the rotor lies in the following four highlighted regions.

If θ_{i_est} = -(2π/3) is used for all θ_actual = 0 to 2π, the algorithm fails for following ambiguous regions (when motor saliency is low):

1. θ_actual lies in the range $$\left[\left(-\frac{2\pi }{3}+ \frac{\pi }{2}-0.1\right),\left(-\frac{2\pi }{3}+ \frac{\pi }{2}+0.1\right)\right]$$

2. θ_actual lies in the range $$\left[\left(-\frac{2\pi }{3}- \frac{\pi }{2}-0.1\right),\left(-\frac{2\pi }{3}- \frac{\pi }{2}+0.1\right)\right]$$

3. θ_actual lies in the range $$\left[\left(-\frac{2\pi }{3}+\pi -0.1\right),\left(-\frac{2\pi }{3}+ \pi +0.1\right)\right]$$

Because these ambiguous regions are not present in the preceding four regions, you can eliminate the regions where the algorithm might fail.

Therefore, using this approach you have three sets of regions corresponding to three different initial estimates. These three sets of regions cover all the motor sectors where the rotor can lie:

In part A, the block picks the θ_{i_est} corresponding to the maximum i_q peak current value between i_q1, i_q2, and i_q3 for Part B.

Part B: Pulsating High-Frequency (PHF) Method

After determining the best possible initial estimate θ_{i_est}, the block injects a sinusoidal high-frequency voltage (with peak amplitude V_phf and frequency f_h) along the finalized (θ_est | t = 0) = θ_{i_est} and reads the q-axis current response of the motor as described in Part A. However, in addition, it applies signal processing routines on the q-axis current response to make corrections to θ_est using a PI controller in a closed-loop configuration as shown below:

The following steps describe the signal processing routines used by the block:

1. Multiply the measured i_q with cosine signal (with unit amplitude and frequency f_h) to obtain the following signal:

   $$i_q\cos \left({\omega }_{h}t\right)$$

2. Apply low-pass filter (LPF) to extract the bias term in the preceding result.

3. Negate the output of step 2.

From the output of the preceding 3 steps, we can derive the following error signal:

$$Error\_signal=\frac{V_{phf}\left(L_q-L_d\right)\sin (2{\theta }_{err})}{8\pi f_h{L}_d{L}_q}$$

Because we can approximate sin(θ) to θ (when θ is close to zero), we can derive the following approximated error signal after considering that θerr is close to zero:

$$Error\_signal\_approximated=\frac{V_{phf}\left(L_q-L_d\right)}{4\pi f_h{L}_d{L}_q}{\theta }_{err}=\frac{V_{phf}\left(L_q-L_d\right)}{4\pi f_h{L}_d{L}_q}\left({\theta }_{actual}-{\theta }_{est}\right)=G\left({\theta }_{actual}-{\theta }_{est}\right)$$

Therefore, using the preceding result, we can simplify model 1 as shown below:

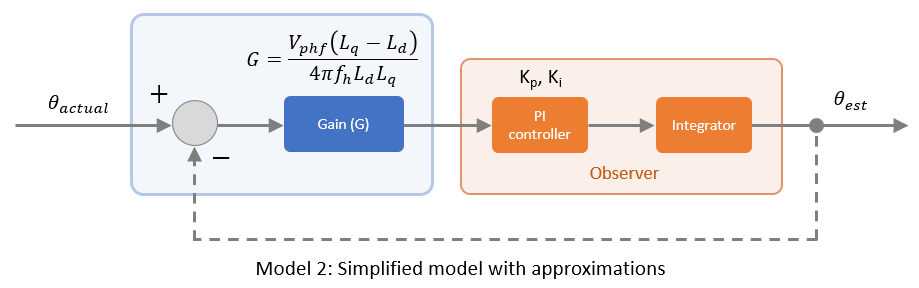
The following term represents the transfer function (simplified) of the entire model:

$$\frac{G{k}_{p}s+G{k}_i}{s^2+G{k}_{p}s+G{k}_i}$$

where, k_p and k_i proportional and integral gains of the PI controller.

Therefore, when the block executes, the estimated position is initially θ_{i_est}, but it rises steadily (dynamically according to G, k_p, and k_i gains) to saturate at a certain angle (with respect to a-axis) such that Error_signal is close to zero.

Note

In Part B, the high frequency voltage signal injection happens for a given time duration (Close loop duration (s) parameter). Select this time duration such that the dynamics of θ_est reaches saturation.

The approximation used earlier introduces a limitation in the PHF method due to which the algorithm might compute the rotor position with an ambiguity of π. If the rotor lies in the range $${\theta }_{actual}=\left(0,\frac{\pi }{2}\right]\cup \left[\frac{3\pi }{2},2\pi \right)$$ electrical radians (region 1), the estimated position is accurate (π compensation is not required).

If the rotor lies in the range $${\theta }_{actual}=\left(\frac{\pi }{2},\frac{3\pi }{2}\right)$$ electrical radians (region 2), the estimated position shows an ambiguity of π (π compensation is required).

Therefore, the block uses the dual-pulse method to determine if the estimated position needs π compensation.

Part C: Dual-Pulse (DP) Method

The block injects two very short duration voltage pulses (with the same width and magnitude) in the following positions:

• Pulse 1 at the rotor position estimated in Part B

• Pulse 2 at the rotor position estimated in Part B + π

Because pulse width is very short, the motor does not run, and the rotor remains stationary after pulse injection.

The interaction between the resulting stator magnetic flux and the rotor permanent magnets results in two current impulses along the d-axis of the rotor that rise and fall quickly.

Because the stator core is saturated, it shows nonlinear behaviour. A small L_d results in higher current I_d, and a high L_d results in smaller current I_d. Therefore, the I_d current impulses generated by Pulse 1 and Pulse 2 show different peak values.

Note

The pulse duration of the injected voltage pulses is large enough to obtain a measurable difference between the peak current values. At the same time, the duration is not too high, because, when the pulse duration exceeds a certain limit, the rotor may start spinning.

The block computes the difference between the peak values of the two current impulses ΔI_d to determine if the position estimated in Part A needs π compensation.

ΔI_d = |I_d1| - |I_d2|

PHF injection benefits use cases that require the rotor to remain stationary or that require position estimation without starting the motor. The PHF injection technique also benefits use cases where you need to avoid open loop runs to estimate position (before transitioning to closed-loop speed control) or where you require the motor to start directly in the closed-loop mode. The block algorithm in stage 1 algorithm addresses these use cases by estimating the position while keeping the rotor stationary and avoiding an open-loop run.

Compute Algorithm Parameters Using Motor Parameters

Compute PHF Parameters

The following table describes how the block computes the PHF parameters when you select Compute PHF parameters automatically using motor parameters or when you click the Compute PHF parameters button:

PHF Parameter	Expression or Value	Remarks
PHF frequency (Hz), fh	$$\frac{1}{10T_s}$$	Used in both Part A and Part B.
LP filter cutoff frequency (Hz)	$$\begin{array}{l}4\pi f_h\frac{r}{\sqrt{1-r^2}}\\ \text{where, }r=\frac{\pi f_h{L}_d{L}_q{I}_{base}}{500\cdot V_{phf}\left(L_q-L_d\right)}\end{array}$$	Used in Part B.
Proportional gain, kp	$$\frac{\ln \left(20000\right)}{G\cdot T_{settling}}$$	Used in Part B.
Integral gain, ki	$$\frac{G{\left(k_p\right)}^2}{4{\delta }^2}$$	Used in Part B.
Expected settling time (s), Tsettling	$$\frac{100\ln \left(1000\right)L_q}{R_s}$$	Used in Part B.
Expected damping ratio, ẟ	0.99	Used in Part B.
Open loop duration (s)	$$\frac{\ln \left(1000\right)L_q}{R_s}$$	Used in Part A.
Close loop duration (s)	$$\frac{100\ln \left(1000\right)L_q}{R_s}$$	Used in Part B.
Idle time (s)	$$\frac{\ln \left(1000\right)L_q}{R_s}$$	Used in both Part A and Part B.

where:

• T_s is the block sampling time (in seconds).

• L_d and L_q are the d and q axis stator inductances (in Henry).

• I_base is the base current of the motor (in Amperes).

• V_phf is the peak amplitude value of the injected high frequency voltage signal (in Volts).

• R_s is the motor resistance (in Ohms).

Note

The expressions in the preceding table use elements and values based on the reference papers as well as experimental data.

Compute DP Parameters

The following table describes how the block computes the DP parameters when you select Compute DP parameters automatically using motor parameters or when you click the Compute DP parameters button:

DP Parameter	Expression or Value	Remarks
Pulse duration (s), w	$$\frac{0.75L_d}{R_s}$$	Used in Part C.

where:

• L_d is the d-axis stator inductance (in Henry).

• R_s is the motor resistance (in Ohms).

Note

The expression in the preceding table uses elements and values based on the reference papers as well as experimental data.

References

[1] W. Zine, L. Idkhajine, E. Monmasson, Z. Makni, P. Chauvenet, B. Condamin, and A. Bruyere, "Optimisation of HF signal injection parameters for EV applications based on sensorless IPMSM drives", IET Electric Power Applications, Volume 12, Issue 3, March 2018, p. 347 - 356 (doi:10.1049/iet-epa.2017.0228).

[2] Gaolin Wang, Guoqiang Zhang, and Dianguo Xu, "Position Sensorless Control Techniques for Permanent Magnet Synchronous Machine Drives", Springer, Singapore, 2020 p. 41 - 43 (doi: https://doi.org/10.1007/978-981-15-0050-3).

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Fixed-Point Conversion
Design and simulate fixed-point systems using Fixed-Point Designer™.

Version History

Introduced in R2022b