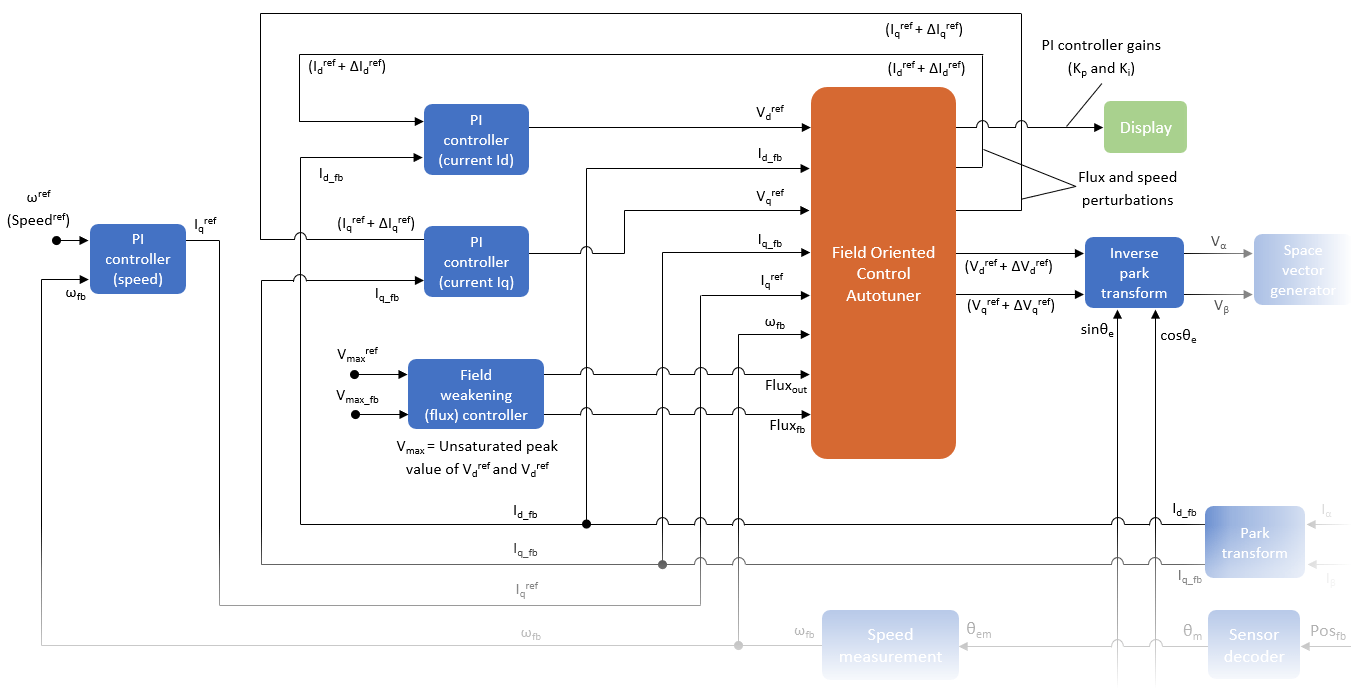
Field Oriented Control Autotuner
Automatically and sequentially tune multiple PID control loops in field-oriented control application

Libraries:
Motor Control Blockset /
Controls /
Controllers
Description
The Field Oriented Control Autotuner block allows you to automatically tune PID control loops in your field-oriented control (FOC) application in real time. For more information on field-oriented control, see Field-Oriented Control (FOC).
You can automatically tune PID controllers associated with the following loops:
Direct-axis (d-axis) current loop
Quadrature-axis (q-axis) current loop
Speed loop
Flux loop
For each loop the block tunes, the Field Oriented Control Autotuner block performs the autotuning experiment in closed-loop without a parametric model associated with that loop. The block allows you to specify the order in which the control loops are tuned. When the tuning experiment is running for one loop, the block has no effect on the other loops. During the experiment, the block:
Injects a test signal into the plant associated with that loop to collect plant input-output data and estimate frequency response in real time. The test signal is combination of sinusoidal perturbation signals added on top of the plant input.
At the end of the experiment, tunes PID controller parameters based on estimated plant frequency responses near the target bandwidth.
Writes updated PID gains at the block output, allowing you to transfer the new gains to existing controllers and validate the closed-loop performance.
You can use the Field Oriented Control Autotuner block to tune the existing PID controllers in your FOC structure. If you do not have the initial PID controllers, you can use the Estimate Control Gains and Use Utility Functions workflow to obtain them. You can then use the Field Oriented Control Autotuner block for refinement or retuning.
If you have a code-generation product such as Simulink® Coder™, you can generate code that implements the tuning algorithm on hardware, letting you tune in real time, using or without using Simulink to manage the autotuning process.
If you have a machine modeled in Simulink with Motor Control Blockset™ and an initial FOC structure with PID controllers, you can perform closed-loop PID autotuning against the modeled machine. Doing so lets you preview the plant response and adjust the settings for PID autotuning before tuning the controller in real time.
The block supports code generation with Simulink Coder, Embedded Coder®, and Simulink PLC Coder™. It does not support code generation with HDL Coder™. For real-time applications, deploy the generated code on a rapid prototyping hardware such as Speedgoat® real-time target machine.
For more information about using the Field Oriented Control Autotuner block, see How to Use Field Oriented Control Autotuner Block.
This block requires Simulink Control Design™ software.
Examples
Tune PI Controllers Using Field Oriented Control Autotuner
Computes the gain values of PI controllers available in the speed and current control loops by using the Field Oriented Control Autotuner block. For details about this block, see Field Oriented Control Autotuner. For details about field-oriented control, see Field-Oriented Control (FOC).
Tune PI Controllers Using Field Oriented Control Autotuner Block on Real-Time Systems
Compute the gain values of PI controllers within the speed and current controllers by using the Field Oriented Control Autotuner block.
Tune PI Controllers (in Field-Weakening Control Mode) Using FOC Autotuner Block
Uses the Field Oriented Control Autotuner block to compute the gain values of the PI controllers available in the speed, current, and flux control loops of a field-weakening control algorithm. For details about this block, see Field Oriented Control Autotuner.
Limitations
The block does not support inherited sample time (–1) when the Experiment Mode is set to PRBS.
Ports
Input
This port accepts the output of the d-axis controller
PID_daxis, which is the output of PID controller
that regulates the d-axis current of the motor. The controller generates
the d-axis voltage reference Vd_ref, while the FOC
autotuner block generates perturbations used during the tuning
experiment for the d-axis current loop.

Dependencies
To enable this port, select Tune D-axis current loop.
Data Types: single | double
This port accepts the d-axis current obtained from the measured (sensed or estimated) motor currents.
Dependencies
To enable this port, select Tune D-axis current loop.
Data Types: single | double
This port accepts the output of the q-axis controller
PID_qaxis, which is the output of PID controller
that regulates the q-axis current of the motor. The controller generates
the q-axis voltage reference Vq_ref, while the FOC
autotuner block generates perturbations used during the tuning
experiment for the q-axis current loop.

Dependencies
To enable this port, select Tune Q-axis current loop.
Data Types: single | double
This port accepts the q-axis current obtained from the measured (sensed or estimated) motor currents.
Dependencies
To enable this port, select Tune Q-axis current loop.
Data Types: single | double
This port accepts the output of the speed controller
PID_speed, which is the output of PID controller
that regulates the speed of the motor. The controller generates the
q-axis current reference Iq_ref, while the FOC
autotuner block generates perturbations used during the tuning
experiment for the speed loop.

Dependencies
To enable this port, select Tune speed loop.
Data Types: single | double
This port accepts the measured (sensed or estimated) speed from the motor.
Dependencies
To enable this port, select Tune speed loop.
Data Types: single | double
This port accepts the output of the flux controller
PID_flux, which is the output of PID controller
that regulates the flux of the motor. The controller generates the
d-axis current reference Id_ref, while the FOC
autotuner block generates perturbations used during the tuning
experiment for the flux loop.

For a permanent magnet synchronous motor (PMSM), there is no flux loop
controller as the rotor flux is fixed and Id_ref is
set to zero. In some applications you can provide a negative
Id_ref value to implement field-weakening control
and achieve higher rotor speeds at the cost of a higher current.
Dependencies
To enable this port, select Tune flux loop.
Data Types: single | double
This port accepts the measured (sensed or estimated) flux from the motor.
Dependencies
To enable this port, select Tune flux loop.
Data Types: single | double
To externally start and stop the autotuning process, provide a signal at the
start/stop port and the
ActiveLoop port.
The experiment starts when the value of the signal changes from negative or zero to positive.
The experiment stops when the value of the signal changes from positive to negative or zero.
For the duration of the experiment, for each loop, the block injects sinusoidal perturbations at the plant input associated with the loop, near the nominal operating point, to collect input-output data and estimate frequency response. When the experiment stops, the block computes PID gains based on the plant frequency responses estimated near the target bandwidth.
When the experiment is not running, the block does not inject any perturbations at the plant inputs. In this state, the block has no impact on plant or controller behavior.
Typically, you can use a signal that changes from 0 to 1 to start the
experiment, and from 1 to 0 to stop it. Consider the following when you
configure the start/stop signal.
Start the experiment when the motor is at the desired equilibrium operating point. Use the initial controller to drive the motor to the operating point.
Avoid any input or output disturbance on the motor during the experiment. If your existing closed-loop system has good disturbance rejection, then the experiment can handle small disturbances. Otherwise, large disturbances can distort the plant output and reduce the accuracy of the frequency-response estimation.
Let the experiment run long enough for the algorithm to collect sufficient data for a good estimate at all frequencies it probes. There are two ways to determine when to stop the experiment:
Determine the experiment duration in advance. A conservative estimate for the experiment duration is 200/ωc in superposition experiment mode or 550/ωc in sinestream experiment mode, where ωc is your target bandwidth.
Observe the signal at the
convergenceoutput, and stop the experiment when the signal stabilizes near 100%.
For PRBS mode, based on the specified Target bandwidth and Controller sample time values, the block dialog displays the recommended experiment length in the Description section of the Experiment tab. Stopping experiment prematurely may lead to incorrect tuning results. (since R2024a)
When you stop the experiment, the block computes tuned PID gains and updates the signal at the
pid gainsport.
You can configure any logic appropriate for your application to
control the start and stop times of the experiment. The
start/stop signal is specified along with
ActiveLoop. ActiveLoop takes
integer values 1 to 4 and specifies which loop to tune.
Alternatively, if you are tuning in simulation or external mode, you can specify the tuning experiment sequence, start time and duration in the block parameters.
Dependencies
To enable this port, on the Block tab under Parameters Source, select Use external source for start/stop of experiment.
Data Types: single | double
Set the ActiveLoop value to specify which loop to
tune when providing an external source for the start and stop times of
the tuning experiment.
ActiveLoop Value | Loop to Tune |
|---|---|
1 | D-axis current loop |
2 | Q-axis current loop |
3 | Speed loop |
4 | Flux loop |
You can configure any logic appropriate for your application along
with the start/stop port to control the sequence and
the time at which the loop tuning experiment runs.
ActiveLoop takes integer values from 1 to 4 and
specifies which loop to tune. Any other number will result in no tuning
taking place regardless of the start/stop signal. For
example, when you supply a constant value 2 at
ActiveLoop and the signal at
start/stop rises, the block starts the tuning
experiment for the q-axis current loop.
Alternatively, you can specify the tuning experiment sequence, start time, and duration in the block parameters.
Dependencies
To enable this port, on the Block tab under Parameters Source, select Use external source for start/stop of experiment.
Data Types: single | double
Supply the values for the Target bandwidth (rad/sec) parameter for
each loop to be tuned. If you are tuning multiple loops, you can specify
the bandwidth as a vector or bus, entries of which correspond to the
target bandwidth for the loops in this order:
D-axis current loop
Q-axis current loop
Speed loop
Flux loop
The vector signal must be specified as a N-by-1 or 1-by-N signal or if specified as a bus must have N elements, where N is the number of loops to be tuned. For instance, if you are tuning the q-axis current loop and the speed loop, and you specify a vector [5000, 200] at this port, the block tunes the q-axis current controller with the target bandwidth 5000 rad/sec and the speed loop controller with the target bandwidth 200 rad/sec.
If you are tuning multiple loops and specify a scalar value at this port, then the block uses the same target bandwidth to tune all the controllers. For effective cascade control, the inner control loops (d-axis and q-axis) must respond much faster than the outer control loops (flux and speed). Therefore, you must supply the target bandwidth as a vector or bus signal when tuning multiple loops.
Alternatively, you can specify target bandwidth for individual loops in block parameters. For more information on how to choose a bandwidth, see that parameter description.
Dependencies
To enable this port, on the Block tab under Parameters Source, select Use external source for bandwidth.
Data Types: single | double
Supply a value for the Target phase margin (degrees) parameter for
each loop to be tuned. If you are tuning multiple loops, you can specify
target PM as a vector or bus, entries of which
correspond to the target phase margin for the loops in this
order:
D-axis current loop
Q-axis current loop
Speed loop
Flux loop
The vector signal must be specified as a N-by-1 or 1-by-N signal or if specified as a bus must have N elements, where N is the number of loops to be tuned. For instance, if you are tuning q-axis current loop and speed loop, and you specify a vector [60, 45] at this port, the block tunes q-axis current controller with target phase margin 60 degrees and speed loop controller with target phase margin 45 degrees.
If you are tuning multiple loops and specify a scalar value at this port, then the block uses the same target phase margin to tune all the controllers.
Alternatively, you can specify target phase margin for individual loops in block parameters. For more information on how to choose a target phase margin, see that parameter description.
Dependencies
To enable this port, on the Block tab under Parameters Source, select Use external source for target phase margin.
Data Types: single | double
Supply a value for the Sine Amplitudes parameter for each loop to
be tuned. Specify one of the following:
Vector of length 5 to specify a different amplitude at each of [1/10, 1/3, 1, 3, 10]ωc , where ωc is the target bandwidth for tuning.
N-by-5 matrix, where N is the number of loops to be tuned. Each row entry must be of length 5 to specify a different amplitude at each of [1/10, 1/3, 1, 3, 10]ωc .
If you are tuning multiple loops and specify a vector of length 5 at this port, then the block uses the specified amplitude for all the loops at each of [1/10, 1/3, 1, 3, 10]ωc corresponding to that loop.
Alternatively, you can specify the sinusoidal perturbation amplitude for individual loops in block parameters. For more information, see the parameter description.
Dependencies
To enable this port, on the Block tab under Parameters Source, select Use external source for sine amplitudes.
Data Types: single | double
Output
Perturbation signal input used for estimating the frequency-response data model associated with the d-axis current control loop. Inject the perturbation signal from this port by using a sum block to the output of the PID controller that regulates the d-axis current.
When the experiment is running, the block generates perturbation signals at this port.
When the experiment is not running, the signal at this port is zero. In this state, the block has no effect on the plant.
Dependencies
To enable this port, select Tune D-axis current loop.
Data Types: single | double
Perturbation signal input used for estimating the frequency-response data model associated with the q-axis current control loop. Inject this perturbation signal from this port by using a sum block to the output of the PID controller that regulates the q-axis current.
When the experiment is running, the block generates perturbation signals at this port.
When the experiment is not running, the signal at this port is zero. In this state, the block has no effect on the plant.
Dependencies
To enable this port, select Tune Q-axis current loop.
Data Types: single | double
Perturbation signal input used for estimating the frequency-response data model associated with the motor speed control loop. Inject this perturbation signal from this port by using a sum block with the output of the PID controller that regulates the speed of the motor.
When the experiment is running, the block generates perturbation signals at this port.
When the experiment is not running, the signal at this port is zero. In this state, the block has no effect on the plant.
Dependencies
To enable this port, select Tune speed loop.
Data Types: single | double
Perturbation signal input used for estimating the frequency-response data model associated with the motor flux control loop. Inject this perturbation signal from this port by using a sum block to the output of the PID controller that regulates the flux linkage of the motor.
When the experiment is running, the block generates perturbation signals at this port.
When the experiment is not running, the signal at this port is zero. In this state, the block has no effect on the plant.
Dependencies
To enable this port, select Tune flux loop.
Data Types: single | double
This 4-element bus signal contains the tuned PID gains P,
I, D, and the filter
coefficient N for each control loop the block tunes.
These values correspond to the P,
I, D, and N
parameters in the expressions given in the Form
parameter. Initially, the values are 0, 0, 0, and 100, respectively. The
block updates the values when the experiment ends. The bus signal
corresponding to each loop the block tunes always has four elements,
even if you are not tuning a PIDF controller.
Data Types: single | double
The block uses perturbation signals to estimate the frequency response
of the plant associated with each loop at several frequencies around the
target bandwidth for tuning. convergence indicates
how close to completion the estimation of the plant frequency response
is. Typically, this value quickly rises to about 90% after the
experiment begins, and then gradually converges to a higher value. Stop
the experiment when it levels off near 100%.
For PRBS experiment mode, the signal at this port updates only after the estimation experiment has finished. (since R2024a)
Data Types: single | double
This port outputs the estimated phase margin achieved by the tuned controller for the
most recently tuned loop, in degrees. The block updates this value when
the tuning experiment ends for each loop. The estimated phase margin is
calculated from the angle of
G(jωc)C(jωc),
where G is the estimated plant for that loop,
C is the tuned controller, and
ωc is the crossover
frequency (bandwidth). The estimated phase margin might differ from the
target phase margin specified by the Target phase margin
(degrees) parameter. It is an indicator of the robustness
and stability achieved by the tuned system.
Typically, the estimated phase margin is near the target phase margin. In general, the larger the value, the more robust is the tuned system, and the less overshoot there is.
A negative phase margin indicates that the closed-loop system might be unstable.
Dependencies
To enable this port, on the Block tab, select Estimated phase margin achieved by tuned controllers.
Data Types: single | double
This port outputs the frequency-response data estimated by the experiment for most
recently tuned loop. Initially, the value at frd is
[0, 0, 0, 0, 0]. During the experiment, the block injects signals at
frequencies [1/10, 1/3, 1, 3,
10]ωc, where ωc is
the target bandwidth. At each sample time during the experiment, the
block updates frd with a vector containing the
complex frequency response at each of these frequencies. You can use the
progress of the response as an alternative to
convergence to examine the convergence of the
estimation. When the experiment stops, the block updates
frd with the final estimated frequency response
used for computing the PID gains.
For PRBS experiment mode, the signal at this port updates only after the estimation experiment has finished. (since R2024a)
Dependencies
To enable this port, on the Block tab, select Plant frequency responses near bandwidth.
Data Types: single | double
This port outputs a vector containing the plant input and plant output for the most recently tuned loop or the loop currently being tuned. These values are the plant input and output at the nominal operating point at which the block performs the experiment.
Dependencies
To enable this port, on the Block tab, select Plant nominal input and output.
Data Types: single | double
This 4-element bus signal indicates whether the tuning experiment for each loop tuned by
the block is active or not. For each signal in the bus, the port outputs
the logical value 1 (true) for the
loop when the tuning experiment is running. The value is logical
0 (false) when the experiment
is over or has not yet started. You can use this port to trigger updates
of PID gains for individual loops.
Dependencies
To enable this port, on the Block tab, disable Use external source for start/stop of experiment and select Start/stop of autotuning process.
Data Types: single | double
Parameters
Use this parameter to enable or disable d-axis current loop autotuning.
Programmatic Use
Block Parameter:
TuneDaxisLoop |
| Type: character vector |
Values:
'on' | 'off'
|
Default:
'on' |
Use this parameter to enable or disable q-axis current loop autotuning.
Programmatic Use
Block Parameter:
TuneQaxisLoop |
| Type: character vector |
Values:
'on' | 'off'
|
Default:
'on' |
Use this parameter to enable or disable speed loop autotuning.
Programmatic Use
Block Parameter:
TuneSpeedLoop |
| Type: character vector |
Values:
'on' | 'off'
|
Default:
'on' |
Use this parameter to enable or disable flux loop autotuning.
Programmatic Use
Block Parameter:
TuneSpeedLoop |
| Type: character vector |
Values:
'on' | 'off'
|
Default:
'on' |
Select this parameter to enable the same tuning and experiment settings for d-axis and q-axis current loops. When enabled, the block uses the same controller settings, target bandwidth, phase margin, and other experiment settings to tune d-axis and q-axis current loops.
Programmatic Use
Block Parameter:
UseSameSettingsInner |
| Type: character vector |
Values:
'off' | 'on'
|
Default:
'off' |
Select this parameter to enable the same tuning and experiment settings for speed and flux loops. When enabled, the block uses the same controller settings, target bandwidth, phase margin, and other experiment settings to tune speed and flux loops.
Programmatic Use
Block Parameter:
UseSameSettingsOuter |
| Type: character vector |
Values:
'off' | 'on'
|
Default:
'off' |
Specify the sample time of the frequency response estimation experiment performed by the block in seconds.
By default, the experiment sample time is set to inherited (–1) and the block performs the frequency response estimation experiment, for each loop, at the inherited sample time. Use this parameter to specify a sample time for the frequency response estimation experiment that is different from the tuning and PID gain calculation sample rates. For each loop that you tune, the frequency responses are estimated at the sample time specified in this parameter.
When you specify different sample times for tuning, experiment, and loops, you can configure Simulink to treat each block module rate as a separate task to enable multitasking execution for your model. This multitasking mode helps improve performance on hardware. For more information, see Treat each discrete rate as a separate task.
Programmatic Use
Block Parameter:
TsExperiment |
| Type: scalar |
| Value positive scalar |
| Default: –1 (inherited) |
Tuning Tab
By default, the block runs tuning for each loop at the same sample time that you specify in the Controller sample time (sec) parameter for that loop. Enable this parameter to run tuning at a sample rate that is different from the sample rate of the PID controllers you are tuning and the frequency response estimation experiment performed by the block. The PID gain tuning algorithm is computationally intensive, and when you want to deploy the block to hardware and tune a controller with a fast sample time, some hardware might not complete the PID gain calculation in a single time step. To reduce the hardware throughput requirements, specify a tuning sample time slower than the controller sample time using the Tuning sample time (sec) parameter.
Programmatic Use
Block Parameter:
UseTuningTs |
| Type: character vector |
Value
'off' | 'on' |
Default:
'off' |
Specify the sample time of the tuning algorithm in seconds.
If you intend to deploy the block on hardware with limited processing power and want to tune a controller with a fast sample time, specify a sample time such that the tuning algorithm runs at a slower rate than the PID controllers you are tuning. For each loop that you tune, after the frequency response estimation experiment ends, controller tuning occurs at the sample time specified in this parameter.
Dependencies
To enable this parameter, select Use different sample time for tuning.
Programmatic Use
Block Parameter:
TsTuning |
| Type: scalar |
| Value positive scalar |
| Default: 0.2 |
D-axis Current Loop
Specify the type of PID controller associated with the d-axis current control loop.
The controller type indicates what actions are present in the controller that regulates the loop. The following controller types are available for PID autotuning:
P— Proportional onlyI— Integral onlyPI— Proportional and integralPD— Proportional and derivativePDF— Proportional and derivative with derivative filterPID— Proportional, integral, and derivativePIDF— Proportional, integral, and derivative with derivative filter
Make sure the controller type matches the controller that regulates the loop.
Programmatic Use
Block Parameter:
PIDTypeDaxis |
| Type: character vector |
Values:
'P' | 'I' |
'PI' | 'PD' |
'PDF' | 'PID' |
'PIDF' |
Default:
'PI' |
Specify the PID controller form associated with your d-axis current control loop.
The controller form determines the interpretation of the PID coefficients P, I, D, and N.
Parallel— InParallelform, the transfer function of a discrete-time PIDF controller iswhere Fi(z) and Fd(z) are the integrator and filter formulas (see
Integrator methodandFilter method).Other controller actions amount to setting P, I, or D to zero.
Ideal— InIdealform, the transfer function of a discrete-time PIDF controller isOther controller actions amount to setting D to zero or setting I to
Inf. (In ideal form, the controller must have proportional action.)
Make sure the controller form matches the controller that regulates the loop.
Programmatic Use
Block Parameter:
PIDFormDaxis |
| Type: character vector |
Values:
'Parallel' |
'Ideal' |
Default:
'Parallel' |
Tunable: Yes
Specify the sample time of your PID controller associated with the d-axis current control loop in seconds. This parameter sets the sample time used to calculate the PID controller gains for the loop.
To perform PID tuning, the block measures frequency-response information up to a frequency of
10 times the target bandwidth. To ensure that this frequency is less than the Nyquist
frequency, the target bandwidth ωc must satisfy ωcTs
≤ 0.3, where Ts
ωc is the controller sample time that you specify
with the Controller sample time (sec) parameter.
Make sure the controller sample time matches the controller that regulates the loop.
Tips
If you want to run the deployed block with different sample times in your application, set this parameter to –1 and put the block in a Triggered Subsystem. Then, trigger the subsystem at the desired sample time. If you do not plan to change the sample time after deployment, specify a fixed and finite sample time.
Programmatic Use
Block Parameter:
TsDaxis |
| Type: scalar |
| Value positive scalar | –1 |
| Default: 0.001 |
Specify the discrete integration formula for the integrator term in your controller. In discrete time, the PID controller transfer function assumed by the block is
in parallel form, or in ideal form,
For a controller sample time Ts, the
Integrator method parameter determines the formula
Fi as follows.
| Integrator method | Fi |
|---|---|
Forward Euler |
|
Backward Euler |
|
Trapezoidal |
|
For more information about the relative advantages of each method, see the Discrete PID Controller block reference page.
Make sure the controller integrator method matches the controller that regulates the loop.
Dependencies
This parameter is enabled when the controller includes integral action.
Programmatic Use
Block Parameter:
IntegratorMethodDaxis |
| Type: character vector |
Values:
'Forward Euler' | 'Backward
Euler' | 'Trapezoidal' |
Default:
'Forward Euler' |
Tunable: Yes
Specify the discrete integration formula for the derivative filter term in your controller. In discrete time, the PID controller transfer function assumed by the block is
in parallel form, or in ideal form,
For a controller sample time Ts, the
Filter method parameter determines the formula
Fd as follows.
| Filter method | Fd |
|---|---|
Forward Euler |
|
Backward Euler |
|
Trapezoidal |
|
For more information about the relative advantages of each method, see the Discrete PID Controller block reference page.
Make sure the controller derivative filter method matches the controller that regulates the loop.
Dependencies
This parameter is enabled when the controller includes derivative action with a derivative filter term.
Programmatic Use
Block Parameter:
FilterMethodDaxis |
| Type: character vector |
Values:
'Forward Euler' | 'Backward
Euler' | 'Trapezoidal' |
Default:
'Forward Euler' |
Tunable: Yes
The target bandwidth is the target value for the 0 dB gain crossover frequency of the tuned open-loop response CP, where P is the plant response associated with the loop, and C is the controller response. This crossover frequency roughly sets the control bandwidth. For a rise time τ seconds, a good guess for the target bandwidth is 2/τ rad/sec.
To perform PID tuning, the autotuner block measures frequency-response information up to a frequency of 10 times the target bandwidth. To ensure that this frequency is less than the Nyquist frequency, the target bandwidth ωc must satisfy ωcTs ≤ 0.3, where Ts is the controller sample time that you specify with the Controller sample time (sec) parameter. Because of this condition, the fastest rise time you can enforce for tuning is about 6.67Ts. If this rise time does not meet your design goals, consider reducing Ts.
For best results, use a target bandwidth that is within about a factor of 10 of the bandwidth with the initial PID controller. To tune a controller for a larger change in bandwidth, tune incrementally using smaller changes.
To provide the target bandwidth by using an input port, on the Block tab, select Use external source for bandwidth.
Programmatic Use
Block Parameter:
BandwidthDaxis |
| Type: positive scalar |
Default:
100 |
Specify a target minimum phase margin for the tuned open-loop response associated with the d-axis current control loop at the crossover frequency.
The target phase margin reflects the desired robustness of the tuned system. Typically, choose a value in the range of about 45°–60°. In general, a higher phase margin reduces overshoot, but can limit the response speed. The default value 60° tends to balance performance and robustness, yielding about 5–10% overshoot, depending on the characteristics of your plant.
To provide the target phase margin by using an input port, on the Block tab, select Use external source for target phase margins.
Tunable: Yes
Programmatic Use
Block Parameter:
TargetPMDaxis |
| Type: scalar |
| Values: 0–90 |
| Default: 60 |
Q-axis Current Loop
Specify the type of PID controller associated with the q-axis current control loop.
The controller type indicates what actions are present in the controller that regulates the loop. The following controller types are available for PID autotuning:
P— Proportional onlyI— Integral onlyPI— Proportional and integralPD— Proportional and derivativePDF— Proportional and derivative with derivative filterPID— Proportional, integral, and derivativePIDF— Proportional, integral, and derivative with derivative filter
Make sure the controller type matches the controller that regulates the loop.
Programmatic Use
Block Parameter:
PIDTypeQaxis |
| Type: character vector |
Values:
'P' | 'I' |
'PI' | 'PD' |
'PDF' | 'PID' |
'PIDF' |
Default:
'PI' |
Specify the PID controller form associated with your q-axis current control loop.
The controller form determines the interpretation of the PID coefficients P, I, D, and N.
Parallel— InParallelform, the transfer function of a discrete-time PIDF controller iswhere Fi(z) and Fd(z) are the integrator and filter formulas (see
Integrator methodandFilter method).Other controller actions amount to setting P, I, or D to zero.
Ideal— InIdealform, the transfer function of a discrete-time PIDF controller isOther controller actions amount to setting D to zero or setting I to
Inf. (In ideal form, the controller must have proportional action.)
Make sure the controller form matches the controller that regulates the loop.
Programmatic Use
Block Parameter:
PIDFormQaxis |
| Type: character vector |
Values:
'Parallel' |
'Ideal' |
Default:
'Parallel' |
Tunable: Yes
Specify the sample time of your PID controller associated with the q-axis current control loop in seconds. This parameter sets the sample time used to calculate the PID controller gains for the loop.
To perform PID tuning, the block measures frequency-response information up to a frequency of
10 times the target bandwidth. To ensure that this frequency is less than the Nyquist
frequency, the target bandwidth ωc must satisfy ωcTs
≤ 0.3, where Ts
ωc is the controller sample time that you specify
with the Controller sample time (sec) parameter.
Make sure the controller sample time matches the controller that regulates the loop.
Tips
If you want to run the deployed block with different sample times in your application, set this parameter to –1 and put the block in a Triggered Subsystem. Then, trigger the subsystem at the desired sample time. If you do not plan to change the sample time after deployment, specify a fixed and finite sample time.
Programmatic Use
Block Parameter:
TsQaxis |
| Type: scalar |
| Value positive scalar | –1 |
| Default: 0.001 |
Specify the discrete integration formula for the integrator term in your controller. In discrete time, the PID controller transfer function assumed by the block is
in parallel form, or in ideal form,
For a controller sample time Ts, the
Integrator method parameter determines the formula
Fi as follows.
| Integrator method | Fi |
|---|---|
Forward Euler |
|
Backward Euler |
|
Trapezoidal |
|
For more information about the relative advantages of each method, see the Discrete PID Controller block reference page.
Make sure the controller integrator method matches the controller that regulates the loop.
Dependencies
This parameter is enabled when the controller includes integral action.
Programmatic Use
Block Parameter:
IntegratorMethodQaxis |
| Type: character vector |
Values:
'Forward Euler' | 'Backward
Euler' | 'Trapezoidal' |
Default:
'Forward Euler' |
Tunable: Yes
Specify the discrete integration formula for the derivative filter term in your controller. In discrete time, the PID controller transfer function assumed by the block is
in parallel form, or in ideal form,
For a controller sample time Ts, the
Filter method parameter determines the formula
Fd as follows.
| Filter method | Fd |
|---|---|
Forward Euler |
|
Backward Euler |
|
Trapezoidal |
|
For more information about the relative advantages of each method, see the Discrete PID Controller block reference page.
Make sure the controller derivative filter method matches the controller that regulates the loop.
Dependencies
This parameter is enabled when the controller includes derivative action with a derivative filter term.
Programmatic Use
Block Parameter:
FilterMethodQaxis |
| Type: character vector |
Values:
'Forward Euler' | 'Backward
Euler' | 'Trapezoidal' |
Default:
'Forward Euler' |
Tunable: Yes
The target bandwidth is the target value for the 0 dB gain crossover frequency of the tuned open-loop response CP, where P is the plant response associated with the loop, and C is the controller response. This crossover frequency roughly sets the control bandwidth. For a rise time τ seconds, a good guess for the target bandwidth is 2/τ rad/sec.
To perform PID tuning, the autotuner block measures frequency-response information up to a frequency of 10 times the target bandwidth. To ensure that this frequency is less than the Nyquist frequency, the target bandwidth ωc must satisfy ωcTs ≤ 0.3, where Ts is the controller sample time that you specify with the Controller sample time (sec) parameter. Because of this condition, the fastest rise time you can enforce for tuning is about 6.67Ts. If this rise time does not meet your design goals, consider reducing Ts.
For best results, use a target bandwidth that is within about a factor of 10 of the bandwidth with the initial PID controller. To tune a controller for a larger change in bandwidth, tune incrementally using smaller changes.
To provide the target bandwidth by using an input port, on the Block tab, select Use external source for bandwidth.
Programmatic Use
Block Parameter:
BandwidthQaxis |
| Type: positive scalar |
Default:
100 |
Specify a target minimum phase margin for the tuned open-loop response associated with the q-axis current control loop at the crossover frequency.
The target phase margin reflects the desired robustness of the tuned system. Typically, choose a value in the range of about 45°–60°. In general, a higher phase margin reduces overshoot, but can limit the response speed. The default value 60° tends to balance performance and robustness, yielding about 5–10% overshoot, depending on the characteristics of your plant.
To provide the target phase margin by using an input port, on the Block tab, select Use external source for target phase margins.
Tunable: Yes
Programmatic Use
Block Parameter:
TargetPMQaxis |
| Type: scalar |
| Values: 0–90 |
| Default: 60 |
Speed Loop
Specify the type of PID controller associated with the speed control loop.
The controller type indicates what actions are present in the controller that regulates the loop. The following controller types are available for PID autotuning:
P— Proportional onlyI— Integral onlyPI— Proportional and integralPD— Proportional and derivativePDF— Proportional and derivative with derivative filterPID— Proportional, integral, and derivativePIDF— Proportional, integral, and derivative with derivative filter
Make sure the controller type matches the controller that regulates the loop.
Programmatic Use
Block Parameter:
PIDTypeSpeed |
| Type: character vector |
Values:
'P' | 'I' |
'PI' | 'PD' |
'PDF' | 'PID' |
'PIDF' |
Default:
'PI' |
Specify the PID controller form associated with your speed control loop.
The controller form determines the interpretation of the PID coefficients P, I, D, and N.
Parallel— InParallelform, the transfer function of a discrete-time PIDF controller iswhere Fi(z) and Fd(z) are the integrator and filter formulas (see
Integrator methodandFilter method).Other controller actions amount to setting P, I, or D to zero.
Ideal— InIdealform, the transfer function of a discrete-time PIDF controller isOther controller actions amount to setting D to zero or setting I to
Inf. (In ideal form, the controller must have proportional action.)
Make sure the controller form matches the controller that regulates the loop.
Programmatic Use
Block Parameter:
PIDFormSpeed |
| Type: character vector |
Values:
'Parallel' |
'Ideal' |
Default:
'Parallel' |
Tunable: Yes
Specify the sample time of your PID controller associated with the speed control loop in seconds. This parameter sets the sample time used to calculate the PID controller gains for the loop.
To perform PID tuning, the block measures frequency-response information up to a frequency of
10 times the target bandwidth. To ensure that this frequency is less than the Nyquist
frequency, the target bandwidth ωc must satisfy ωcTs
≤ 0.3, where Ts
ωc is the controller sample time that you specify
with the Controller sample time (sec) parameter.
Make sure the controller sample time matches the controller that regulates the loop.
Tips
If you want to run the deployed block with different sample times in your application, set this parameter to –1 and put the block in a Triggered Subsystem. Then, trigger the subsystem at the desired sample time. If you do not plan to change the sample time after deployment, specify a fixed and finite sample time.
Programmatic Use
Block Parameter:
TsSpeed |
| Type: scalar |
| Value positive scalar | –1 |
| Default: 0.1 |
Specify the discrete integration formula for the integrator term in your controller. In discrete time, the PID controller transfer function assumed by the block is
in parallel form, or in ideal form,
For a controller sample time Ts, the
Integrator method parameter determines the formula
Fi as follows.
| Integrator method | Fi |
|---|---|
Forward Euler |
|
Backward Euler |
|
Trapezoidal |
|
For more information about the relative advantages of each method, see the Discrete PID Controller block reference page.
Make sure the controller integrator method matches the controller that regulates the loop.
Dependencies
This parameter is enabled when the controller includes integral action.
Programmatic Use
Block Parameter:
IntegratorMethodSpeed |
| Type: character vector |
Values:
'Forward Euler' | 'Backward
Euler' | 'Trapezoidal' |
Default:
'Forward Euler' |
Tunable: Yes
Specify the discrete integration formula for the derivative filter term in your controller. In discrete time, the PID controller transfer function assumed by the block is
in parallel form, or in ideal form,
For a controller sample time Ts, the
Filter method parameter determines the formula
Fd as follows.
| Filter method | Fd |
|---|---|
Forward Euler |
|
Backward Euler |
|
Trapezoidal |
|
For more information about the relative advantages of each method, see the Discrete PID Controller block reference page.
Make sure the controller derivative filter method matches the controller that regulates the loop.
Dependencies
This parameter is enabled when the controller includes derivative action with a derivative filter term.
Programmatic Use
Block Parameter:
FilterMethodSpeed |
| Type: character vector |
Values:
'Forward Euler' | 'Backward
Euler' | 'Trapezoidal' |
Default:
'Forward Euler' |
Tunable: Yes
The target bandwidth is the target value for the 0 dB gain crossover frequency of the tuned open-loop response CP, where P is the plant response associated with the loop, and C is the controller response. This crossover frequency roughly sets the control bandwidth. For a rise time τ seconds, a good guess for the target bandwidth is 2/τ rad/sec.
To perform PID tuning, the autotuner block measures frequency-response information up to a frequency of 10 times the target bandwidth. To ensure that this frequency is less than the Nyquist frequency, the target bandwidth ωc must satisfy ωcTs ≤ 0.3, where Ts is the controller sample time that you specify with the Controller sample time (sec) parameter. Because of this condition, the fastest rise time you can enforce for tuning is about 6.67Ts. If this rise time does not meet your design goals, consider reducing Ts.
For best results, use a target bandwidth that is within about a factor of 10 of the bandwidth with the initial PID controller. To tune a controller for a larger change in bandwidth, tune incrementally using smaller changes.
To provide the target bandwidth by using an input port, on the Block tab, select Use external source for bandwidth.
Programmatic Use
Block Parameter:
BandwidthSpeed |
| Type: positive scalar |
Default:
1 |
Specify a target minimum phase margin for the tuned open-loop response associated with the speed control loop at the crossover frequency.
The target phase margin reflects the desired robustness of the tuned system. Typically, choose a value in the range of about 45°–60°. In general, a higher phase margin reduces overshoot, but can limit the response speed. The default value 60° tends to balance performance and robustness, yielding about 5–10% overshoot, depending on the characteristics of your plant.
To provide the target phase margin by using an input port, on the Block tab, select Use external source for target phase margins.
Tunable: Yes
Programmatic Use
Block Parameter:
TargetPMSpeed |
| Type: scalar |
| Values: 0–90 |
| Default: 60 |
Flux Loop
Specify the type of PID controller associated with the flux control loop.
The controller type indicates what actions are present in the controller that regulates the loop. The following controller types are available for PID autotuning:
P— Proportional onlyI— Integral onlyPI— Proportional and integralPD— Proportional and derivativePDF— Proportional and derivative with derivative filterPID— Proportional, integral, and derivativePIDF— Proportional, integral, and derivative with derivative filter
Make sure the controller type matches the controller that regulates the loop.
Programmatic Use
Block Parameter:
PIDTypeFlux |
| Type: character vector |
Values:
'P' | 'I' |
'PI' | 'PD' |
'PDF' | 'PID' |
'PIDF' |
Default:
'PI' |
Specify the PID controller form associated with your flux control loop.
The controller form determines the interpretation of the PID coefficients P, I, D, and N.
Parallel— InParallelform, the transfer function of a discrete-time PIDF controller iswhere Fi(z) and Fd(z) are the integrator and filter formulas (see
Integrator methodandFilter method).Other controller actions amount to setting P, I, or D to zero.
Ideal— InIdealform, the transfer function of a discrete-time PIDF controller isOther controller actions amount to setting D to zero or setting I to
Inf. (In ideal form, the controller must have proportional action.)
Make sure the controller form matches the controller that regulates the loop.
Programmatic Use
Block Parameter:
PIDFormFlux |
| Type: character vector |
Values:
'Parallel' |
'Ideal' |
Default:
'Parallel' |
Tunable: Yes
Specify the sample time of your PID controller associated with the flux control loop in seconds. This parameter sets the sample time used to calculate the PID controller gains for the loop.
To perform PID tuning, the block measures frequency-response information up to a frequency of
10 times the target bandwidth. To ensure that this frequency is less than the Nyquist
frequency, the target bandwidth ωc must satisfy ωcTs
≤ 0.3, where Ts
ωc is the controller sample time that you specify
with the Controller sample time (sec) parameter.
Make sure the controller sample time matches the controller that regulates the loop.
Tips
If you want to run the deployed block with different sample times in your application, set this parameter to –1 and put the block in a Triggered Subsystem. Then, trigger the subsystem at the desired sample time. If you do not plan to change the sample time after deployment, specify a fixed and finite sample time.
Programmatic Use
Block Parameter:
TsFlux |
| Type: scalar |
| Value positive scalar | –1 |
| Default: 0.1 |
Specify the discrete integration formula for the integrator term in your controller. In discrete time, the PID controller transfer function assumed by the block is
in parallel form, or in ideal form,
For a controller sample time Ts, the
Integrator method parameter determines the formula
Fi as follows.
| Integrator method | Fi |
|---|---|
Forward Euler |
|
Backward Euler |
|
Trapezoidal |
|
For more information about the relative advantages of each method, see the Discrete PID Controller block reference page.
Make sure the controller integrator method matches the controller that regulates the loop.
Dependencies
This parameter is enabled when the controller includes integral action.
Programmatic Use
Block Parameter:
IntegratorMethodFlux |
| Type: character vector |
Values:
'Forward Euler' | 'Backward
Euler' | 'Trapezoidal' |
Default:
'Forward Euler' |
Tunable: Yes
Specify the discrete integration formula for the derivative filter term in your controller. In discrete time, the PID controller transfer function assumed by the block is
in parallel form, or in ideal form,
For a controller sample time Ts, the
Filter method parameter determines the formula
Fd as follows.
| Filter method | Fd |
|---|---|
Forward Euler |
|
Backward Euler |
|
Trapezoidal |
|
For more information about the relative advantages of each method, see the Discrete PID Controller block reference page.
Make sure the controller derivative filter method matches the controller that regulates the loop.
Dependencies
This parameter is enabled when the controller includes derivative action with a derivative filter term.
Programmatic Use
Block Parameter:
FilterMethodFlux |
| Type: character vector |
Values:
'Forward Euler' | 'Backward
Euler' | 'Trapezoidal' |
Default:
'Forward Euler' |
Tunable: Yes
The target bandwidth is the target value for the 0 dB gain crossover frequency of the tuned open-loop response CP, where P is the plant response associated with the loop, and C is the controller response. This crossover frequency roughly sets the control bandwidth. For a rise time τ seconds, a good guess for the target bandwidth is 2/τ rad/sec.
To perform PID tuning, the autotuner block measures frequency-response information up to a frequency of 10 times the target bandwidth. To ensure that this frequency is less than the Nyquist frequency, the target bandwidth ωc must satisfy ωcTs ≤ 0.3, where Ts is the controller sample time that you specify with the Controller sample time (sec) parameter. Because of this condition, the fastest rise time you can enforce for tuning is about 6.67Ts. If this rise time does not meet your design goals, consider reducing Ts.
For best results, use a target bandwidth that is within about a factor of 10 of the bandwidth with the initial PID controller. To tune a controller for a larger change in bandwidth, tune incrementally using smaller changes.
To provide the target bandwidth by using an input port, on the Block tab, select Use external source for bandwidth.
Programmatic Use
Block Parameter:
BandwidthFlux |
| Type: positive scalar |
Default:
1 |
Specify a target minimum phase margin for the tuned open-loop response associated with the flux control loop at the crossover frequency.
The target phase margin reflects the desired robustness of the tuned system. Typically, choose a value in the range of about 45°–60°. In general, a higher phase margin reduces overshoot, but can limit the response speed. The default value 60° tends to balance performance and robustness, yielding about 5–10% overshoot, depending on the characteristics of your plant.
To provide the target phase margin by using an input port, on the Block tab, select Use external source for target phase margins.
Tunable: Yes
Programmatic Use
Block Parameter:
TargetPMFlux |
| Type: scalar |
| Values: 0–90 |
| Default: 60 |
Current Loops (Q-axis + D-axis)
Specify the type of PID controller associated with the current control loops.
The controller type indicates what actions are present in the controller that regulates the loop. The following controller types are available for PID autotuning:
P— Proportional onlyI— Integral onlyPI— Proportional and integralPD— Proportional and derivativePDF— Proportional and derivative with derivative filterPID— Proportional, integral, and derivativePIDF— Proportional, integral, and derivative with derivative filter
Make sure the controller type matches the controller that regulates the loop.
Programmatic Use
Block Parameter:
PIDTypeAllInner |
| Type: character vector |
Values:
'P' | 'I' |
'PI' | 'PD' |
'PDF' | 'PID' |
'PIDF' |
Default:
'PI' |
Specify the PID controller form associated with your current control loops.
The controller form determines the interpretation of the PID coefficients P, I, D, and N.
Parallel— InParallelform, the transfer function of a discrete-time PIDF controller iswhere Fi(z) and Fd(z) are the integrator and filter formulas (see
Integrator methodandFilter method).Other controller actions amount to setting P, I, or D to zero.
Ideal— InIdealform, the transfer function of a discrete-time PIDF controller isOther controller actions amount to setting D to zero or setting I to
Inf. (In ideal form, the controller must have proportional action.)
Make sure the controller form matches the controller that regulates the loop.
Programmatic Use
Block Parameter:
PIDFormAllInner |
| Type: character vector |
Values:
'Parallel' |
'Ideal' |
Default:
'Parallel' |
Tunable: Yes
Specify the sample time of your PID controllers associated with the current control loops in seconds. This parameter sets the sample time used to calculate the PID controller gains for the loop.
To perform PID tuning, the block measures frequency-response information up to a frequency of
10 times the target bandwidth. To ensure that this frequency is less than the Nyquist
frequency, the target bandwidth ωc must satisfy ωcTs
≤ 0.3, where Ts
ωc is the controller sample time that you specify
with the Controller sample time (sec) parameter.
Make sure the controller sample time matches the controller that regulates the loop.
Tips
If you want to run the deployed block with different sample times in your application, set this parameter to –1 and put the block in a Triggered Subsystem. Then, trigger the subsystem at the desired sample time. If you do not plan to change the sample time after deployment, specify a fixed and finite sample time.
Programmatic Use
Block Parameter:
TsAllInner |
| Type: scalar |
| Value positive scalar | –1 |
| Default: 0.001 |
Specify the discrete integration formula for the integrator term in your controller. In discrete time, the PID controller transfer function assumed by the block is
in parallel form, or in ideal form,
For a controller sample time Ts, the
Integrator method parameter determines the formula
Fi as follows.
| Integrator method | Fi |
|---|---|
Forward Euler |
|
Backward Euler |
|
Trapezoidal |
|
For more information about the relative advantages of each method, see the Discrete PID Controller block reference page.
Make sure the controller integrator method matches the controller that regulates the loop.
Dependencies
This parameter is enabled when the controller includes integral action.
Programmatic Use
Block Parameter:
IntegratorMethodAllInner |
| Type: character vector |
Values:
'Forward Euler' | 'Backward
Euler' | 'Trapezoidal' |
Default:
'Forward Euler' |
Tunable: Yes
Specify the discrete integration formula for the derivative filter term in your controller. In discrete time, the PID controller transfer function assumed by the block is
in parallel form, or in ideal form,
For a controller sample time Ts, the
Filter method parameter determines the formula
Fd as follows.
| Filter method | Fd |
|---|---|
Forward Euler |
|
Backward Euler |
|
Trapezoidal |
|
For more information about the relative advantages of each method, see the Discrete PID Controller block reference page.
Make sure the controller derivative filter method matches the controller that regulates the loop.
Dependencies
This parameter is enabled when the controller includes derivative action with a derivative filter term.
Programmatic Use
Block Parameter:
FilterMethodAllInner |
| Type: character vector |
Values:
'Forward Euler' | 'Backward
Euler' | 'Trapezoidal' |
Default:
'Forward Euler' |
Tunable: Yes
The target bandwidth is the target value for the 0 dB gain crossover frequency of the tuned open-loop response CP, where P is the plant response associated with the loop, and C is the controller response. This crossover frequency roughly sets the control bandwidth. For a rise time τ seconds, a good guess for the target bandwidth is 2/τ rad/sec.
To perform PID tuning, the autotuner block measures frequency-response information up to a frequency of 10 times the target bandwidth. To ensure that this frequency is less than the Nyquist frequency, the target bandwidth ωc must satisfy ωcTs ≤ 0.3, where Ts is the controller sample time that you specify with the Controller sample time (sec) parameter. Because of this condition, the fastest rise time you can enforce for tuning is about 6.67Ts. If this rise time does not meet your design goals, consider reducing Ts.
For best results, use a target bandwidth that is within about a factor of 10 of the bandwidth with the initial PID controller. To tune a controller for a larger change in bandwidth, tune incrementally using smaller changes.
To provide the target bandwidth by using an input port, on the Block tab, select Use external source for bandwidth.
Programmatic Use
Block Parameter:
BandwidthAllInner |
| Type: positive scalar |
Default:
1 |
Specify target minimum phase margin for the tuned open-loop responses associated with the current control loops at the crossover frequency.
The target phase margin reflects the desired robustness of the tuned system. Typically, choose a value in the range of about 45°–60°. In general, a higher phase margin reduces overshoot, but can limit the response speed. The default value 60° tends to balance performance and robustness, yielding about 5–10% overshoot, depending on the characteristics of your plant.
To provide the target phase margin by using an input port, on the Block tab, select Use external source for target phase margins.
Tunable: Yes
Programmatic Use
Block Parameter:
TargetPMAllInner |
| Type: scalar |
| Values: 0–90 |
| Default: 60 |
Outer Loops (Speed + Flux)
Specify the type of PID controllers associated with the outer control loops.
The controller type indicates what actions are present in the controller that regulates the loop. The following controller types are available for PID autotuning:
P— Proportional onlyI— Integral onlyPI— Proportional and integralPD— Proportional and derivativePDF— Proportional and derivative with derivative filterPID— Proportional, integral, and derivativePIDF— Proportional, integral, and derivative with derivative filter
Make sure the controller type matches the controller that regulates the loop.
Programmatic Use
Block Parameter:
PIDTypeAllOuter |
| Type: character vector |
Values:
'P' | 'I' |
'PI' | 'PD' |
'PDF' | 'PID' |
'PIDF' |
Default:
'PI' |
Specify the PID controller form associated with your outer control loops.
The controller form determines the interpretation of the PID coefficients P, I, D, and N.
Parallel— InParallelform, the transfer function of a discrete-time PIDF controller iswhere Fi(z) and Fd(z) are the integrator and filter formulas (see
Integrator methodandFilter method).Other controller actions amount to setting P, I, or D to zero.
Ideal— InIdealform, the transfer function of a discrete-time PIDF controller isOther controller actions amount to setting D to zero or setting I to
Inf. (In ideal form, the controller must have proportional action.)
Make sure the controller form matches the controller that regulates the loop.
Programmatic Use
Block Parameter:
PIDFormAllOuter |
| Type: character vector |
Values:
'Parallel' |
'Ideal' |
Default:
'Parallel' |
Tunable: Yes
Specify the sample time of your PID controllers associated with the outer control loop in seconds. This parameter sets the sample time used to calculate the PID controller gains for the loop.
To perform PID tuning, the block measures frequency-response information up to a frequency of
10 times the target bandwidth. To ensure that this frequency is less than the Nyquist
frequency, the target bandwidth ωc must satisfy ωcTs
≤ 0.3, where Ts
ωc is the controller sample time that you specify
with the Controller sample time (sec) parameter.
Make sure the controller sample time matches the controller that regulates the loop.
Tips
If you want to run the deployed block with different sample times in your application, set this parameter to –1 and put the block in a Triggered Subsystem. Then, trigger the subsystem at the desired sample time. If you do not plan to change the sample time after deployment, specify a fixed and finite sample time.
Programmatic Use
Block Parameter:
TsAllOuter |
| Type: scalar |
| Value positive scalar | –1 |
| Default: 0.1 |
Specify the discrete integration formula for the integrator term in your controller. In discrete time, the PID controller transfer function assumed by the block is
in parallel form, or in ideal form,
For a controller sample time Ts, the
Integrator method parameter determines the formula
Fi as follows.
| Integrator method | Fi |
|---|---|
Forward Euler |
|
Backward Euler |
|
Trapezoidal |
|
For more information about the relative advantages of each method, see the Discrete PID Controller block reference page.
Make sure the controller integrator method matches the controller that regulates the loop.
Dependencies
This parameter is enabled when the controller includes integral action.
Programmatic Use
Block Parameter:
IntegratorMethodAllOuter |
| Type: character vector |
Values:
'Forward Euler' | 'Backward
Euler' | 'Trapezoidal' |
Default:
'Forward Euler' |
Tunable: Yes
Specify the discrete integration formula for the derivative filter term in your controller. In discrete time, the PID controller transfer function assumed by the block is
in parallel form, or in ideal form,
For a controller sample time Ts, the
Filter method parameter determines the formula
Fd as follows.
| Filter method | Fd |
|---|---|
Forward Euler |
|
Backward Euler |
|
Trapezoidal |
|
For more information about the relative advantages of each method, see the Discrete PID Controller block reference page.
Make sure the controller derivative filter method matches the controller that regulates the loop.
Dependencies
This parameter is enabled when the controller includes derivative action with a derivative filter term.
Programmatic Use
Block Parameter:
FilterMethodAllOuter |
| Type: character vector |
Values:
'Forward Euler' | 'Backward
Euler' | 'Trapezoidal' |
Default:
'Forward Euler' |
Tunable: Yes
The target bandwidth is the target value for the 0 dB gain crossover frequency of the tuned open-loop response CP, where P is the plant response associated with the loop, and C is the controller response. This crossover frequency roughly sets the control bandwidth. For a rise time τ seconds, a good guess for the target bandwidth is 2/τ rad/sec.
To perform PID tuning, the autotuner block measures frequency-response information up to a frequency of 10 times the target bandwidth. To ensure that this frequency is less than the Nyquist frequency, the target bandwidth ωc must satisfy ωcTs ≤ 0.3, where Ts is the controller sample time that you specify with the Controller sample time (sec) parameter. Because of this condition, the fastest rise time you can enforce for tuning is about 6.67Ts. If this rise time does not meet your design goals, consider reducing Ts.
For best results, use a target bandwidth that is within about a factor of 10 of the bandwidth with the initial PID controller. To tune a controller for a larger change in bandwidth, tune incrementally using smaller changes.
To provide the target bandwidth by using an input port, on the Block tab, select Use external source for bandwidth.
Programmatic Use
Block Parameter:
BandwidthAllOuter |
| Type: positive scalar |
Default:
1 |
Specify a target minimum phase margin for the tuned open-loop responses associated with the outer control loops at the crossover frequency.
The target phase margin reflects the desired robustness of the tuned system. Typically, choose a value in the range of about 45°–60°. In general, a higher phase margin reduces overshoot, but can limit the response speed. The default value 60° tends to balance performance and robustness, yielding about 5–10% overshoot, depending on the characteristics of your plant.
To provide the target phase margin by using an input port, on the Block tab, select Use external source for target phase margins.
Tunable: Yes
Programmatic Use
Block Parameter:
TargetPMAllOuter |
| Type: scalar |
| Values: 0–90 |
| Default: 60 |
Experiment Tab
Experiment Start/Stop
Specify the simulation time when the d-axis current loop tuning experiment starts.
Programmatic Use
Block Parameter:
StartTimeDaxis |
| Type: positive scalar |
| Default: 1 |
Specify the d-axis current loop tuning experiment duration.
Programmatic Use
Block Parameter:
DurationDaxis |
| Type: positive scalar |
| Default: 0.05 |
Specify the simulation time when the q-axis current loop tuning experiment starts.
Programmatic Use
Block Parameter:
StartTimeQaxis |
| Type: positive scalar |
| Default: 1.1 |
Specify the q-axis current loop tuning experiment duration.
Programmatic Use
Block Parameter:
DurationQaxis |
| Type: positive scalar |
| Default: 0.05 |
Specify the simulation time when the speed loop tuning experiment starts.
Programmatic Use
Block Parameter:
StartTimeSpeed |
| Type: positive scalar |
| Default: 2 |
Specify the speed loop tuning experiment duration.
Programmatic Use
Block Parameter:
DurationSpeed |
| Type: positive scalar |
| Default: 3 |
Specify the simulation time when the flux tuning experiment starts.
Programmatic Use
Block Parameter:
StartTimeFlux |
| Type: positive scalar |
| Default: 6 |
Specify the flux loop tuning experiment duration.
Programmatic Use
Block Parameter:
DurationFlux |
| Type: positive scalar |
| Default: 3 |
Loop Experiment Settings
Specify whether the perturbation at each frequency is applied as sequential sinusoidal (Sinestream), simultaneous sinusoidal (Superposition), or pseudorandom binary sequence (PRBS).
Sinestream — In this mode, the block applies perturbation at each frequency separately. For more information about sinestream signals for estimation, see Sinestream Input Signals (Simulink Control Design).
Superposition — In this mode, the perturbation signal includes all specified frequencies at once. For frequency response estimation at a vector of frequencies ω = [ω1, … , ωN] at amplitudes A = [A1, … , AN], the perturbation signal is:
PRBS — A deterministic pseudorandom binary sequence that shifts between two values and has white-noise-like properties. PRBS signals reduce total estimation time compared to using sinestream input signals, while producing comparable estimation results. PRBS signals are useful for estimating frequency responses for communications and power electronics systems. For more information, see PRBS Input Signals (Simulink Control Design). (since R2024a)
Sinestream mode can be more accurate and can also be less intrusive, because the total size of the perturbation is never bigger than the values specified by the Sine Amplitudes parameter. However, due to the sequential nature of the sinestream perturbation, each frequency point you add increases the recommended experiment time (see the start/stop input port for details). Thus, the estimation experiment is typically much faster in Superposition mode with satisfactory results.
Sinestream signals reduce the execution time compared to superposition input signals, but also take longer to estimate the frequency response. Frequency response estimation using sinestream signals is useful when you have limited processing power and you want to reduce the execution time.
To cover a similar frequency range, the experiment length in PRBS mode is typically much shorter than the other two modes. However, there is a tradeoff between the speed and quality of results. (since R2024a)
Programmatic Use
Block Parameter:
ExperimentMode |
| Type: character vector |
Values:
'Superposition' |
'Sinestream' | 'PRBS'
|
Default:
'Superposition' |
D-axis Current Loop
Specify whether the plant associated with the d-axis current control
loop is stable or integrating. If the plant has one or more integrators,
select Integrating.
Programmatic Use
Block Parameter:
PlantTypeDaxis |
| Type: character vector |
Values:
'Stable' |
'Integrating' |
Default:
'Stable' |
Specify whether the plant associated with the d-axis current control
loop is positive or negative. If a positive change in the plant input at
the nominal operating point results in a positive change in the plant
output, specify Positive. Otherwise, specify
negative. For stable plants, the sign of the plant is the sign of the
plant DC gain.
Programmatic Use
Block Parameter:
PlantSignDaxis |
| Type: character vector |
Values:
'Positive' |
'Negative' |
Default:
'Positive' |
During the experiment, the block injects a sinusoidal signal into the plant associated with the loop at the frequencies [1/10, 1/3, 1, 3, 10]ωc , where ωc is the target bandwidth for tuning. Use Sine Amplitudes to specify the amplitude of each of these injected signals. Specify a:
Scalar value to inject the same amplitude at each frequency
Vector of length 5 to specify a different amplitude at each of [1/10, 1/3, 1, 3, 10]ωc
In a typical plant with typical target bandwidth, the magnitudes of the plant responses at the experiment frequencies do not vary widely. In such cases, you can use a scalar value to apply the same magnitude perturbation at all frequencies. However, if you know that the response decays sharply over the frequency range, consider decreasing the amplitude of the lower frequency inputs and increasing the amplitude of the higher frequency inputs. It is numerically better for the estimation experiment when all the plant responses have comparable magnitudes.
The perturbation amplitudes must be:
Large enough that the perturbation overcomes any deadband in the plant actuator and generates a response above the noise level
Small enough to keep the plant running within the approximately linear region near the nominal operating point, and to avoid saturating the plant input or output
When Experiment mode is Superposition, the sinusoidal signals are superimposed. Thus, the perturbation can be at least as large as the sum of all amplitudes. Make sure that the largest possible perturbation is within the range of your plant actuator. Saturating the actuator can introduce errors into the estimated frequency response.
To provide the sine amplitudes by using an input port, on the Block tab, select Use external source for sine amplitudes.
Tunable: Yes
Programmatic Use
Block Parameter:
AmpSineDaxis |
| Type: scalar, vector of length 5 |
| Default: 1 |
Q-axis Current Loop
Specify whether the plant associated with the q-axis current control
loop is stable or integrating. If the plant has one or more integrators,
select Integrating.
Programmatic Use
Block Parameter:
PlantTypeQaxis |
| Type: character vector |
Values:
'Stable' |
'Integrating' |
Default:
'Stable' |
Specify whether the plant associated with the q-axis current control
loop is positive or negative. If a positive change in the plant input at
the nominal operating point results in a positive change in the plant
output, specify Positive. Otherwise, specify
negative. For stable plants, the sign of the plant is the sign of the
plant DC gain.
Programmatic Use
Block Parameter:
PlantSignQaxis |
| Type: character vector |
Values:
'Positive' |
'Negative' |
Default:
'Positive' |
During the experiment, the block injects a sinusoidal signal into the plant associated with the loop at the frequencies [1/10, 1/3, 1, 3, 10]ωc , where ωc is the target bandwidth for tuning. Use Sine Amplitudes to specify the amplitude of each of these injected signals. Specify a:
Scalar value to inject the same amplitude at each frequency
Vector of length 5 to specify a different amplitude at each of [1/10, 1/3, 1, 3, 10]ωc
In a typical plant with typical target bandwidth, the magnitudes of the plant responses at the experiment frequencies do not vary widely. In such cases, you can use a scalar value to apply the same magnitude perturbation at all frequencies. However, if you know that the response decays sharply over the frequency range, consider decreasing the amplitude of the lower frequency inputs and increasing the amplitude of the higher frequency inputs. It is numerically better for the estimation experiment when all the plant responses have comparable magnitudes.
The perturbation amplitudes must be:
Large enough that the perturbation overcomes any deadband in the plant actuator and generates a response above the noise level
Small enough to keep the plant running within the approximately linear region near the nominal operating point, and to avoid saturating the plant input or output
When Experiment mode is Superposition, the sinusoidal signals are superimposed. Thus, the perturbation can be at least as large as the sum of all amplitudes. Make sure that the largest possible perturbation is within the range of your plant actuator. Saturating the actuator can introduce errors into the estimated frequency response.
To provide the sine amplitudes by using an input port, on the Block tab, select Use external source for sine amplitudes.
Tunable: Yes
Programmatic Use
Block Parameter:
AmpSineQaxis |
| Type: scalar, vector of length 5 |
| Default: 1 |
Speed Loop
Specify whether the plant associated with the speed control loop is
stable or integrating. If the plant has one or more integrators, select
Integrating.
Programmatic Use
Block Parameter:
PlantTypeSpeed |
| Type: character vector |
Values:
'Stable' |
'Integrating' |
Default:
'Stable' |
Specify whether the plant associated with the speed control loop is
positive or negative. If a positive change in the plant input at the
nominal operating point results in a positive change in the plant
output, specify Positive. Otherwise, specify
negative. For stable plants, the sign of the plant is the sign of the
plant DC gain.
Programmatic Use
Block Parameter:
PlantSignSpeed |
| Type: character vector |
Values:
'Positive' |
'Negative' |
Default:
'Positive' |
During the experiment, the block injects a sinusoidal signal into the plant associated with the loop at the frequencies [1/10, 1/3, 1, 3, 10]ωc , where ωc is the target bandwidth for tuning. Use Sine Amplitudes to specify the amplitude of each of these injected signals. Specify a:
Scalar value to inject the same amplitude at each frequency
Vector of length 5 to specify a different amplitude at each of [1/10, 1/3, 1, 3, 10]ωc
In a typical plant with typical target bandwidth, the magnitudes of the plant responses at the experiment frequencies do not vary widely. In such cases, you can use a scalar value to apply the same magnitude perturbation at all frequencies. However, if you know that the response decays sharply over the frequency range, consider decreasing the amplitude of the lower frequency inputs and increasing the amplitude of the higher frequency inputs. It is numerically better for the estimation experiment when all the plant responses have comparable magnitudes.
The perturbation amplitudes must be:
Large enough that the perturbation overcomes any deadband in the plant actuator and generates a response above the noise level
Small enough to keep the plant running within the approximately linear region near the nominal operating point, and to avoid saturating the plant input or output
When Experiment mode is Superposition, the sinusoidal signals are superimposed. Thus, the perturbation can be at least as large as the sum of all amplitudes. Make sure that the largest possible perturbation is within the range of your plant actuator. Saturating the actuator can introduce errors into the estimated frequency response.
To provide the sine amplitudes by using an input port, on the Block tab, select Use external source for sine amplitudes.
Tunable: Yes
Programmatic Use
Block Parameter:
AmpSineSpeed |
| Type: scalar, vector of length 5 |
| Default: 1 |
Flux Loop
Specify whether the plant associated with the flux control loop is
stable or integrating. If the plant has one or more integrators, select
Integrating.
Programmatic Use
Block Parameter:
PlantTypeFlux |
| Type: character vector |
Values:
'Stable' |
'Integrating' |
Default:
'Stable' |
Specify whether the plant associated with the flux control loop is
positive or negative. If a positive change in the plant input at the
nominal operating point results in a positive change in the plant
output, specify Positive. Otherwise, specify
negative. For stable plants, the sign of the plant is the sign of the
plant DC gain.
Programmatic Use
Block Parameter:
PlantSignFlux |
| Type: character vector |
Values:
'Positive' |
'Negative' |
Default:
'Positive' |
During the experiment, the block injects a sinusoidal signal into the plant associated with the loop at the frequencies [1/10, 1/3, 1, 3, 10]ωc , where ωc is the target bandwidth for tuning. Use Sine Amplitudes to specify the amplitude of each of these injected signals. Specify a:
Scalar value to inject the same amplitude at each frequency
Vector of length 5 to specify a different amplitude at each of [1/10, 1/3, 1, 3, 10]ωc
In a typical plant with typical target bandwidth, the magnitudes of the plant responses at the experiment frequencies do not vary widely. In such cases, you can use a scalar value to apply the same magnitude perturbation at all frequencies. However, if you know that the response decays sharply over the frequency range, consider decreasing the amplitude of the lower frequency inputs and increasing the amplitude of the higher frequency inputs. It is numerically better for the estimation experiment when all the plant responses have comparable magnitudes.
The perturbation amplitudes must be:
Large enough that the perturbation overcomes any deadband in the plant actuator and generates a response above the noise level
Small enough to keep the plant running within the approximately linear region near the nominal operating point, and to avoid saturating the plant input or output
When Experiment mode is Superposition, the sinusoidal signals are superimposed. Thus, the perturbation can be at least as large as the sum of all amplitudes. Make sure that the largest possible perturbation is within the range of your plant actuator. Saturating the actuator can introduce errors into the estimated frequency response.
To provide the sine amplitudes by using an input port, on the Block tab, select Use external source for sine amplitudes.
Tunable: Yes
Programmatic Use
Block Parameter:
AmpSineFlux |
| Type: scalar, vector of length 5 |
| Default: 1 |
Current Loops (D-axis + Q-axis)
Specify whether the plants associated with the current control loops
are stable or integrating. If the plant has one or more integrators,
select Integrating.
Programmatic Use
Block Parameter:
PlantTypeAllInner |
| Type: character vector |
Values:
'Stable' |
'Integrating' |
Default:
'Stable' |
Specify whether the plants associated with the current control loops
are positive or negative. If a positive change in the plant input at the
nominal operating point results in a positive change in the plant
output, specify Positive. Otherwise, specify
negative. For stable plants, the sign of the plant is the sign of the
plant DC gain.
Programmatic Use
Block Parameter:
PlantSignAllInner |
| Type: character vector |
Values:
'Positive' |
'Negative' |
Default:
'Positive' |
During the experiment, the block injects a sinusoidal signal into the plant associated with the loop at the frequencies [1/10, 1/3, 1, 3, 10]ωc , where ωc is the target bandwidth for tuning. Use Sine Amplitudes to specify the amplitude of each of these injected signals. Specify a:
Scalar value to inject the same amplitude at each frequency
Vector of length 5 to specify a different amplitude at each of [1/10, 1/3, 1, 3, 10]ωc
In a typical plant with typical target bandwidth, the magnitudes of the plant responses at the experiment frequencies do not vary widely. In such cases, you can use a scalar value to apply the same magnitude perturbation at all frequencies. However, if you know that the response decays sharply over the frequency range, consider decreasing the amplitude of the lower frequency inputs and increasing the amplitude of the higher frequency inputs. It is numerically better for the estimation experiment when all the plant responses have comparable magnitudes.
The perturbation amplitudes must be:
Large enough that the perturbation overcomes any deadband in the plant actuator and generates a response above the noise level
Small enough to keep the plant running within the approximately linear region near the nominal operating point, and to avoid saturating the plant input or output
When Experiment mode is Superposition, the sinusoidal signals are superimposed. Thus, the perturbation can be at least as large as the sum of all amplitudes. Make sure that the largest possible perturbation is within the range of your plant actuator. Saturating the actuator can introduce errors into the estimated frequency response.
To provide the sine amplitudes by using an input port, on the Block tab, select Use external source for sine amplitudes.
Tunable: Yes
Programmatic Use
Block Parameter:
AmpSineAllInner |
| Type: scalar, vector of length 5 |
| Default: 1 |
Outer Loops (Speed + Flux)
Specify whether the plants associated with the outer control loops are
stable or integrating. If the plant has one or more integrators, select
Integrating.
Programmatic Use
Block Parameter:
PlantTypeAllOuter |
| Type: character vector |
Values:
'Stable' |
'Integrating' |
Default:
'Stable' |
Specify whether the plants associated with the outer control loops are
positive or negative. If a positive change in the plant input at the
nominal operating point results in a positive change in the plant
output, specify Positive. Otherwise, specify
negative. For stable plants, the sign of the plant is the sign of the
plant DC gain.
Programmatic Use
Block Parameter:
PlantSignAllOuter |
| Type: character vector |
Values:
'Positive' |
'Negative' |
Default:
'Positive' |
During the experiment, the block injects a sinusoidal signal into the plant associated with the loop at the frequencies [1/10, 1/3, 1, 3, 10]ωc , where ωc is the target bandwidth for tuning. Use Sine Amplitudes to specify the amplitude of each of these injected signals. Specify a:
Scalar value to inject the same amplitude at each frequency
Vector of length 5 to specify a different amplitude at each of [1/10, 1/3, 1, 3, 10]ωc
In a typical plant with typical target bandwidth, the magnitudes of the plant responses at the experiment frequencies do not vary widely. In such cases, you can use a scalar value to apply the same magnitude perturbation at all frequencies. However, if you know that the response decays sharply over the frequency range, consider decreasing the amplitude of the lower frequency inputs and increasing the amplitude of the higher frequency inputs. It is numerically better for the estimation experiment when all the plant responses have comparable magnitudes.
The perturbation amplitudes must be:
Large enough that the perturbation overcomes any deadband in the plant actuator and generates a response above the noise level
Small enough to keep the plant running within the approximately linear region near the nominal operating point, and to avoid saturating the plant input or output
When Experiment mode is Superposition, the sinusoidal signals are superimposed. Thus, the perturbation can be at least as large as the sum of all amplitudes. Make sure that the largest possible perturbation is within the range of your plant actuator. Saturating the actuator can introduce errors into the estimated frequency response.
To provide the sine amplitudes by using an input port, on the Block tab, select Use external source for sine amplitudes.
Tunable: Yes
Programmatic Use
Block Parameter:
AmpSineAllOuter |
| Type: scalar, vector of length 5 |
| Default: 1 |
Block Tab
Select this parameter to enable the bandwidth input port of the
block. You can specify the target bandwidth for all the loops the block
tunes at this port. When this parameter is disabled, specify the target
bandwidths at the block parameters. For more details, see the
bandwidth port description.
Programmatic Use
Block Parameter:
UseExternalWc |
| Type: character vector |
Values:
'off' | 'on'
|
Default:
'off' |
Select this parameter to enable the target PM input port of the
block. You can specify the target phase margin for all the loops the
block tunes at this port. When this parameter is disabled, specify the
target phase margins at the block parameters. For more details, see the
target PM port description.
Programmatic Use
Block Parameter:
UseExternalPM |
| Type: character vector |
Values:
'off' | 'on'
|
Default:
'off' |
Select this parameter to enable the start/stop and
ActiveLoop input ports of the block. You can
specify the start and stop of the experiment and which loop the block
tunes at these ports. When this parameter is disabled, specify the start
time and duration of the tuning experiment at the block parameters. For
more details, see the start/stop and
ActiveLoop port descriptions.
Programmatic Use
Block Parameter:
UseExternalSourceStartStop |
| Type: character vector |
Values:
'off' | 'on'
|
Default:
'off' |
Select this parameter to enable the sine Amp input port of the block.
You can specify sinusoidal perturbation amplitude for all the loops the
block tunes at this port. When this parameter is disabled, supply the
sine amplitudes at block parameters. For more details, see the
sine Amp port description.
Programmatic Use
Block Parameter:
UseExternalAmpSine |
| Type: character vector |
Values:
'off' | 'on'
|
Default:
'off' |
Specify the floating-point precision based on the simulation environment or hardware requirements.
Programmatic Use
Block Parameter:
BlockDataType |
| Type: character vector |
Values:
'double' | 'single'
|
Default:
'double' |
Select this parameter to enable the estimated PM
output port of the block. The block returns the phase margin achieved by
the tuned controller of the most recently tuned loop. When this
parameter is disabled, you can see the tuning results by using the
Export to MATLAB parameter. For more details,
see the estimated PM port description.
Programmatic Use
Block Parameter:
UseExternalAchievedPM |
| Type: character vector |
Values:
'off' | 'on'
|
Default:
'off' |
Select this parameter to enable the frd output port of the block. The
block returns the phase margin achieved by the tuned controller of the
most recently tuned loop. When this parameter is disabled, you can see
the tuning results by using the Export to MATLAB
parameter. For more details, see the frd port
description.
Programmatic Use
Block Parameter:
UseExternalFRD |
| Type: character vector |
Values:
'off' | 'on'
|
Default:
'off' |
Select this parameter to enable the nominal output port of the block.
The block returns the plant input and output at the nominal operating
point of the most recently tuned loop. When this parameter is disabled,
you can see the tuning results by using the Export to
MATLAB parameter. For more details, see the port
description.
Programmatic Use
Block Parameter:
UseExternalU0 |
| Type: character vector |
Values:
'off' | 'on'
|
Default:
'off' |
Select this parameter to enable loop start/stops output port of the
block. The block returns a signal indicating the times at which the
autotuning experiment started and ended for each loop tuned by the
block. When this parameter is disabled, you can see the tuning results
by using the Export to MATLAB parameter. For more
details, see the loop start/stops port
description.
Programmatic Use
Block Parameter:
UseExternalActiveLoop |
| Type: character vector |
Values:
'off' | 'on'
|
Default:
'off' |
When you click this button, the block creates a structure in the
MATLAB® workspace containing the experiment and tuning results.
This structure, FOCTuningResult, contains the tuning
results for each loop the block tunes.
Daxis— D-axis current loop tuning resultsQaxis— Q-axis current loop tuning resultsSpeed— Speed loop tuning resultsFlux— Flux loop tuning results
For each loop tuned by the block, the result contains the following fields:
P,I,D,N— Tuned PID gains. The structure contains whichever of these fields are necessary for the controller type you are tuning. For instance, if you are tuning a PI controller, the structure containsPandI, but notDandN.TargetBandwidth— The value you specified in theTarget bandwidth (rad/sec)parameter of the block.TargetPhaseMargin— The value you specified in theTarget phase margin (degrees)parameter of the block.EstimatedPhaseMargin— Estimated phase margin achieved by the tuned system.Controller— The tuned PID controller, returned as apid(for parallel form) orpidstd(for ideal form) model object.Plant— The estimated plant, returned as anfrdmodel object. Thisfrdcontains the response data obtained at the experiment frequencies [1/10, 1/3, 1, 3, 10]ωc.PlantNominal— The plant input and output at the nominal operating point when the experiment begins, specified as a structure with the fieldsu(input) andy(output).
You can export to the MATLAB workspace while the simulation is running, including when running in external mode.
Extended Capabilities
The generated code for this block can be resource heavy. For real-time applications, deploying the code on rapid prototyping hardware, such as the Speedgoat real-time target machine, is recommended.
PLC Code Generation
Generate Structured Text code using Simulink® PLC Coder™.
Version History
Introduced in R2020aThe Field Oriented Control Autotuner block now supports estimation using pseudorandom binary sequence (PRBS) input signals. A PRBS signal is a periodic, deterministic signal with white-noise-like properties that shifts between two values. PRBS signals reduce total estimation time compared to using sinestream or superposition input signals, while producing comparable estimation results. PRBS signals are useful for estimating frequency responses for communications and power electronics applications.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)