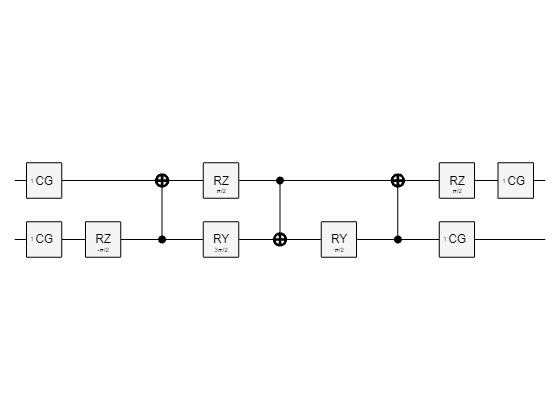
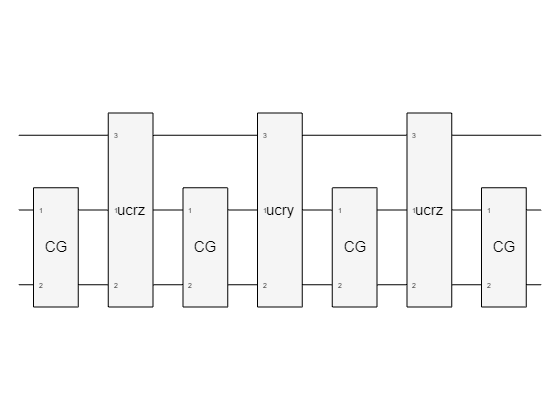
unitaryGate
Installation Required: This functionality requires MATLAB Support Package for Quantum Computing.
Description
cg = unitaryGate(
returns a targetQubits,U)quantum.gate.CompositeGate object that applies a unitary matrix to the target qubits up to a global phase, that is, scaled by a
constant factor.
cg = unitaryGate(
also removes single-qubit rotation gates that have an angle magnitude less than the rotation
threshold.targetQubits,U,RotationThreshold=thresh)
Examples
Input Arguments
More About
Tips
You can use the
unitaryGatefunction to decompose any unitary matrix applied to n target qubits into a composite gate of O(4n) simple quantum gates. However, the resultingCompositeGateobject may not contain the minimal number of gates for an input matrix.
References
[1] Shende, Vivek V., Stephen S. Bullock, and Igor L. Markov. "Synthesis of Quantum Logic Circuits." IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 25, no. 6 (June 2006): 1000–1010. https://doi.org/10.1109/TCAD.2005.855930.
[2] Vatan, Farrokh, and Colin Williams. "Optimal Quantum Circuits for General Two-Qubit Gates." Physical Review A 69, no. 3 (March 22, 2004): 032315. https://doi.org/10.1103/PhysRevA.69.032315.
[3] Drury, Byron, and Peter J. Love. "Constructive Quantum Shannon Decomposition from Cartan Involutions." Journal of Physics A: Mathematical and Theoretical 41, no. 39 (October 3, 2008): 395305. https://doi.org/10.1088/1751-8113/41/39/395305.
Version History
Introduced in R2023b