rref
Reduced row echelon form (Gauss-Jordan elimination)
Description
Examples
Create a matrix and calculate the reduced row echelon form. In this form, the matrix has leading 1s in the pivot position of each column.
A = magic(3)
A = 3×3
8 1 6
3 5 7
4 9 2
RA = rref(A)
RA = 3×3
1 0 0
0 1 0
0 0 1
The 3-by-3 magic square matrix is full rank, so the reduced row echelon form is an identity matrix.
Now, calculate the reduced row echelon form of the 4-by-4 magic square matrix. Specify two outputs to return the nonzero pivot columns. Since this matrix is rank deficient, the result is not an identity matrix.
B = magic(4)
B = 4×4
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
[RB,p] = rref(B)
RB = 4×4
1 0 0 1
0 1 0 3
0 0 1 -3
0 0 0 0
p = 1×3
1 2 3
Use Gauss-Jordan elimination on augmented matrices to solve a linear system and calculate the matrix inverse. These techniques are mainly of academic interest, since there are more efficient and numerically stable ways to calculate these values.
Create a 3-by-3 magic square matrix. Add an additional column to the end of the matrix. This augmented matrix represents a linear system , with the extra column corresponding to .
A = magic(3); A(:,4) = [1; 1; 1]
A = 3×4
8 1 6 1
3 5 7 1
4 9 2 1
Calculate the reduced row echelon form of A. Index into R to extract the entries in the extra (augmented) column, which contains the solution to the linear system.
R = rref(A)
R = 3×4
1.0000 0 0 0.0667
0 1.0000 0 0.0667
0 0 1.0000 0.0667
x = R(:,end)
x = 3×1
0.0667
0.0667
0.0667
A more efficient way to solve this linear system is with the backslash operator, x = A\b.
Create a similar magic square matrix, but this time append an identity matrix of the same size to the end columns.
A = [magic(3) eye(3)]
A = 3×6
8 1 6 1 0 0
3 5 7 0 1 0
4 9 2 0 0 1
Calculate the reduced row echelon form of A. In this form the extra columns contain the inverse matrix for the 3-by-3 magic square matrix.
R = rref(A)
R = 3×6
1.0000 0 0 0.1472 -0.1444 0.0639
0 1.0000 0 -0.0611 0.0222 0.1056
0 0 1.0000 -0.0194 0.1889 -0.1028
inv_A = R(:,4:end)
inv_A = 3×3
0.1472 -0.1444 0.0639
-0.0611 0.0222 0.1056
-0.0194 0.1889 -0.1028
A more efficient way to calculate the inverse matrix is with inv(A).
Consider a linear system of equations with four equations and three unknowns.
Create an augmented matrix that represents the system of equations.
A = [1 1 5;
2 1 8;
1 2 7;
-1 1 -1];
b = [6 8 10 2]';
M = [A b];Use rref to express the system in reduced row echelon form.
R = rref(M)
R = 4×4
1 0 3 2
0 1 2 4
0 0 0 0
0 0 0 0
The first two rows of R contain equations that express and in terms of . The second two rows imply that there exists at least one solution that fits the right-hand side vector (otherwise one of the equations would read ). The third column does not contain a pivot, so is an independent variable. Therefore, there are infinitely many solutions for and , and can be chosen freely.
For example, if , then and .
From a numerical standpoint, a more efficient way to solve this system of equations is with x0 = A\b, which (for a rectangular matrix A) calculates the least-squares solution. In that case, you can check the accuracy of the solution with norm(A*x0-b)/norm(b) and the uniqueness of the solution by checking if rank(A) is equal to the number of unknowns. If more than one solution exists, then they all have the form of , where is the null space null(A) and can be chosen freely.
Input Arguments
Input matrix.
Data Types: single | double
Complex Number Support: Yes
Pivot tolerance, specified as a scalar. If the largest element (by absolute value) in a pivot column is below the tolerance, then the column is zeroed out. This prevents division and multiplication with nonzero pivot elements smaller than the tolerance.
Data Types: single | double
Output Arguments
Reduced row echelon
form of A, returned as a matrix.
Nonzero pivot columns, returned as a vector. Each element in p is
a column index of A. You can use p to estimate
several quantities:
length(p)is an estimate of the rank ofA.x(p)contains the pivot variables in a linear systemAx = b.A(:,p)is a basis for the range ofA.R(1:r,p)is ther-by-ridentity matrix, wherer = length(p).
Limitations
rank,orth, andnullare typically faster and more accurate for computing the rank and basis vectors of a matrix.mldivideis recommended to solve linear systems.
More About
Partial pivoting is the practice of selecting the column element with largest absolute value in the pivot column, and then interchanging the rows of the matrix so that this element is in the pivot position (the leftmost nonzero element in the row).
For example, in the matrix below the algorithm starts by identifying the largest value
in the first column (the value in the (2,1) position equal to 1.1), and
then interchanges the complete first and second rows so that this value appears in the (1,1)
position.
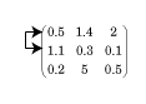
The use of partial pivoting in Gaussian elimination reduces (but does not eliminate) roundoff errors in the calculation.
A matrix is in row echelon form when these conditions are met:
All nonzero rows are above rows of all zeros.
The leading coefficient of each row is strictly to the right of the one in the row above it.
An example of a matrix in row echelon form is
An additional requirement for reduced row echelon form is:
Every leading coefficient must be 1, and must be the only nonzero in its column.
While the identity matrix is most commonly associated with reduced row echelon form, other forms are possible. Another example of a matrix in reduced row echelon form is
Algorithms
rref implements Gauss-Jordan elimination with partial pivoting. A
default tolerance of max(size(A))*eps*norm(A,inf) tests for negligible
column elements that are zeroed-out to reduce roundoff error.
Extended Capabilities
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)