matlab.tall.reduce
Reduce arrays by applying reduction algorithm to blocks of data
Syntax
Description
tA = matlab.tall.reduce(fcn,reducefcn,tX,tY,...)tX,tY,... that are inputs to
fcn. The same rows of each array are operated on by
fcn; for example, fcn(tX(n:m,:),tY(n:m,:)). Inputs
with a height of one are passed to every call of fcn. With this syntax,
fcn must return one output, and reducefcn must
accept one input and return one output.
[
, where tA,tB,...] = matlab.tall.reduce(fcn,reducefcn,tX,tY,...)fcn and reducefcn are functions that return
multiple outputs, returns arrays tA,tB,..., each corresponding to one of
the output arguments of fcn and reducefcn. This syntax
has these requirements:
fcnmust return the same number of outputs as were requested frommatlab.tall.reduce.reducefcnmust have the same number of inputs and outputs as the number of outputs requested frommatlab.tall.reduce.Each output of
fcnandreducefcnmust be the same type as the first inputtX.Corresponding outputs of
fcnandreducefcnmust have the same height.
Examples
Create a tall table, extract a tall vector from the table, and then find the total number of elements in the vector.
Create a tall table for the airlinesmall.csv data set. The data contains information about arrival and departure times of US flights. Extract the ArrDelay variable, which is a vector of arrival delays.
ds = tabularTextDatastore('airlinesmall.csv','TreatAsMissing','NA'); ds.SelectedVariableNames = {'ArrDelay' 'DepDelay'}; tt = tall(ds); tX = tt.ArrDelay;
Use matlab.tall.reduce to count the total number of non-NaN elements in the tall vector. The first function numel counts the number of elements in each block of data, and the second function sum adds together all of the counts for each block to produce a scalar result.
s = matlab.tall.reduce(@numel,@sum,tX)
s =
M×N×... tall double array
? ? ? ...
? ? ? ...
? ? ? ...
: : :
: : :
Preview deferred. Learn more.
Gather the result into memory.
s = gather(s)
Evaluating tall expression using the Local MATLAB Session: - Pass 1 of 1: Completed in 0.65 sec Evaluation completed in 0.81 sec
s = 123523
Create a tall table, extract two tall vectors form the table, and then calculate the mean value of each vector.
Create a tall table for the airlinesmall.csv data set. The data contains information about arrival and departure times of US flights. Extract the ArrDelay and DepDelay variables, which are vectors of arrival and departure delays.
ds = tabularTextDatastore('airlinesmall.csv','TreatAsMissing','NA'); ds.SelectedVariableNames = {'ArrDelay' 'DepDelay'}; tt = tall(ds); tt = rmmissing(tt); tX = tt.ArrDelay; tY = tt.DepDelay;
In the first stage of the algorithm, calculate the sum and element count for each block of data in the vectors. To do this you can write a function that accepts two inputs and returns one output with the sum and count for each input. This function is listed as a local function at the end of the example.
function bx = sumcount(tx,ty) bx = [sum(tx) numel(tx) sum(ty) numel(ty)]; end
In the reduction stage of the algorithm, you need to add together all of the intermediate sums and counts. Thus, matlab.tall.reduce returns the overall sum of elements and number of elements for each input vector, and calculating the mean is then a simple division. For this step you can apply the sum function to the first dimension of the 1-by-4 vector outputs from the first stage.
reducefcn = @(x) sum(x,1); s = matlab.tall.reduce(@sumcount,reducefcn,tX,tY)
s =
M×N×... tall double array
? ? ? ...
? ? ? ...
? ? ? ...
: : :
: : :
Preview deferred. Learn more.
s = gather(s)
Evaluating tall expression using the Local MATLAB Session: - Pass 1 of 1: Completed in 2 sec Evaluation completed in 2.5 sec
s = 1×4
860584 120866 982764 120866
The first two elements of s are the sum and count for tX, and the second two elements are the sum and count for tY. Dividing the sums and counts yields the mean values, which you can compare to the answer returned by the mean function.
my_mean = [s(1)/s(2) s(3)/s(4)]
my_mean = 1×2
7.1201 8.1310
m = gather(mean([tX tY]))
Evaluating tall expression using the Local MATLAB Session: - Pass 1 of 1: Completed in 0.44 sec Evaluation completed in 0.64 sec
m = 1×2
7.1201 8.1310
Local Functions
Listed here is the sumcount function that matlab.tall.reduce calls to calculate the intermediate sums and element counts.
function bx = sumcount(tx,ty) bx = [sum(tx) numel(tx) sum(ty) numel(ty)]; end
Create a tall table, then calculate the mean flight delay for each year in the data.
Create a tall table for the airlinesmall.csv data set. The data contains information about arrival and departure times of US flights. Remove rows of missing data from the table and extract the ArrDelay, DepDelay, and Year variables. These variables are vectors of arrival and departure delays and of the associated years for each flight in the data set.
ds = tabularTextDatastore('airlinesmall.csv','TreatAsMissing','NA'); ds.SelectedVariableNames = {'ArrDelay' 'DepDelay' 'Year'}; tt = tall(ds); tt = rmmissing(tt);
Use matlab.tall.reduce to apply two functions to the tall table. The first function combines the ArrDelay and DepDelay variables to find the total mean delay for each flight. The function determines how many unique years are in each chunk of data, and then cycles through each year and calculates the average total delay for flights in that year. The result is a two-variable table containing the year and mean total delay. This intermediate data needs to be reduced further to arrive at the mean delay per year. Save this function in your current folder as transform_fcn.m.
type transform_fcnfunction t = transform_fcn(a,b,c)
ii = gather(unique(c));
for k = 1:length(ii)
jj = (c == ii(k));
d = mean([a(jj) b(jj)], 2);
if k == 1
t = table(c(jj),d,'VariableNames',{'Year' 'MeanDelay'});
else
t = [t; table(c(jj),d,'VariableNames',{'Year' 'MeanDelay'})];
end
end
end
The second function uses the results from the first function to calculate the mean total delay for each year. The output from reduce_fcn is compatible with the output from transform_fcn, so that blocks of data can be concatenated in any order and continually reduced until only one row remains for each year.
type reduce_fcnfunction TT = reduce_fcn(t)
[groups,Y] = findgroups(t.Year);
D = splitapply(@mean, t.MeanDelay, groups);
TT = table(Y,D,'VariableNames',{'Year' 'MeanDelay'});
end
Apply the transform and reduce functions to the tall vectors. Since the inputs (type double) and outputs (type table) have different data types, use the 'OutputsLike' name-value pair to specify that the output is a table. A simple way to specify the type of the output is to call the transform function with dummy inputs.
a = tt.ArrDelay;
b = tt.DepDelay;
c = tt.Year;
d1 = matlab.tall.reduce(@transform_fcn, @reduce_fcn, a, b, c, 'OutputsLike',{transform_fcn(0,0,0)})d1 =
M×2 tall table
Year MeanDelay
____ _________
? ?
? ?
? ?
: :
: :
Preview deferred. Learn more.
Gather the results into memory to see the mean total flight delay per year.
d1 = gather(d1)
Evaluating tall expression using the Local MATLAB Session: - Pass 1 of 1: Completed in 1.1 sec Evaluation completed in 1.3 sec
d1=22×2 table
Year MeanDelay
____ _________
1987 7.6889
1988 6.7918
1989 8.0757
1990 7.1548
1991 4.0134
1992 5.1767
1993 5.4941
1994 6.0303
1995 8.4284
1996 9.6981
1997 8.4346
1998 8.3789
1999 8.9121
2000 10.595
2001 6.8975
2002 3.4325
⋮
Alternative Approach
Another way to calculate the same statistics by group is to use splitapply to call matlab.tall.reduce (rather than using matlab.tall.reduce to call splitapply).
Using this approach, you call findgroups and splitapply directly on the data. The function mySplitFcn that operates on each group of data includes a call to matlab.tall.reduce. The transform and reduce functions employed by matlab.tall.reduce do not need to group the data, so those functions just perform calculations on the pregrouped data that splitapply passes to them.
type mySplitFcnfunction T = mySplitFcn(a,b,c)
T = matlab.tall.reduce(@non_group_transform_fcn, @non_group_reduce_fcn, ...
a, b, c, 'OutputsLike', {non_group_transform_fcn(0,0,0)});
function t = non_group_transform_fcn(a,b,c)
d = mean([a b], 2);
t = table(c,d,'VariableNames',{'Year' 'MeanDelay'});
end
function TT = non_group_reduce_fcn(t)
D = mean(t.MeanDelay);
TT = table(t.Year(1),D,'VariableNames',{'Year' 'MeanDelay'});
end
end
Call findgroups and splitapply to operate on the data and apply mySplitFcn to each group of data.
groups = findgroups(c); d2 = splitapply(@mySplitFcn, a, b, c, groups); d2 = gather(d2)
Evaluating tall expression using the Local MATLAB Session: - Pass 1 of 2: Completed in 0.35 sec - Pass 2 of 2: Completed in 0.74 sec Evaluation completed in 1.5 sec
d2=22×2 table
Year MeanDelay
____ _________
1987 7.6889
1988 6.7918
1989 8.0757
1990 7.1548
1991 4.0134
1992 5.1767
1993 5.4941
1994 6.0303
1995 8.4284
1996 9.6981
1997 8.4346
1998 8.3789
1999 8.9121
2000 10.595
2001 6.8975
2002 3.4325
⋮
Calculate weighted standard deviation and variance of a tall array using a vector of weights. This is one example of how you can use matlab.tall.reduce to work around functionality that tall arrays do not support yet.
Create two tall vectors of random data. tX contains random data, and tP contains corresponding probabilities such that sum(tP) is 1. These probabilities are suitable to weight the data.
rng default tX = tall(rand(1e4,1)); p = rand(1e4,1); tP = tall(normalize(p,'scale',sum(p)));
Write an identity function that returns outputs equal to the inputs. This approach skips the transform step of matlab.tall.reduce and passes the data directly to the reduction step, where the reduction function is repeatedly applied to reduce the size of the data.
type identityTransform.mfunction [A,B] = identityTransform(X,Y) A = X; B = Y; end
Next, write a reduction function that operates on blocks of the tall vectors to calculate the weighted variance and standard deviation.
type weightedStats.mfunction [wvar, wstd] = weightedStats(X, P) wvar = var(X,P); wstd = std(X,P); end
Use matlab.tall.reduce to apply these functions to the blocks of data in the tall vectors.
[tX_var_weighted, tX_std_weighted] = matlab.tall.reduce(@identityTransform, @weightedStats, tX, tP)
tX_var_weighted =
M×N×... tall double array
? ? ? ...
? ? ? ...
? ? ? ...
: : :
: : :
Preview deferred. Learn more.
tX_std_weighted =
M×N×... tall double array
? ? ? ...
? ? ? ...
? ? ? ...
: : :
: : :
Preview deferred. Learn more.
Input Arguments
Transform function to apply, specified as a function handle or anonymous function.
Each output of fcn must be the same type as the first input
tX. You can use the 'OutputsLike' option to
return outputs of different data types. If fcn returns more than one
output, then the outputs must all have the same height.
The general functional signature of fcn is
[a, b, c, ...] = fcn(x, y, z, ...)
fcn must satisfy these requirements:
Input Arguments — The inputs
[x, y, z, ...]are blocks of data that fit in memory. The blocks are produced by extracting data from the respective tall array inputs[tX, tY, tZ, ...]. The inputs[x, y, z, ...]satisfy these properties:All of
[x, y, z, ...]have the same size in the first dimension after any allowed expansion.The blocks of data in
[x, y, z, ...]come from the same index in the tall dimension, assuming the tall array is nonsingleton in the tall dimension. For example, iftXandtYare nonsingleton in the tall dimension, then the first set of blocks might bex = tX(1:20000,:)andy = tY(1:20000,:).If the first dimension of any of
[tX, tY, tZ, ...]has a size of1, then the corresponding block[x, y, z, ...]consists of all the data in that tall array.
Output Arguments — The outputs
[a, b, c, ...]are blocks that fit in memory, to be sent to the respective outputs[tA, tB, tC, ...]. The outputs[a, b, c, ...]satisfy these properties:All of
[a, b, c, ...]must have the same size in the first dimension.All of
[a, b, c, ...]are vertically concatenated with the respective results of previous calls tofcn.All of
[a, b, c, ...]are sent to the same index in the first dimension in their respective destination output arrays.
Functional Rules —
fcnmust satisfy the functional rule:F([inputs1; inputs2]) == [F(inputs1); F(inputs2)]: Applying the function to the concatenation of the inputs should be the same as applying the function to the inputs separately and then concatenating the results.
Empty Inputs — Ensure that
fcncan handle an input that has a height of 0. Empty inputs can occur when a file is empty or if you have done a lot of filtering on the data.
For example, this function accepts two input arrays, squares them, and returns two output arrays:
function [xx,yy] = sqInputs(x,y) xx = x.^2; yy = y.^2; end
tX and tY and find the maximum value with this
command:tA = matlab.tall.reduce(@sqInputs, @max, tX, tY)
Example: tC = matlab.tall.reduce(@numel,@sum,tX,tY) finds the
number of elements in each block, and then it sums the results to count the total number
of elements.
Data Types: function_handle
Reduction function to apply, specified as a function handle or anonymous function.
Each output of reducefcn must be the same type as the first input
tX. You can use the 'OutputsLike' option to
return outputs of different data types. If reducefcn returns more
than one output, then the outputs must all have the same height.
The general functional signature of reducefcn is
[rA, rB, rC, ...] = reducefcn(a, b, c, ...)
reducefcn must satisfy these requirements:
Input Arguments — The inputs
[a, b, c, ...]are blocks that fit in memory. The blocks of data are either outputs returned byfcn, or a partially reduced output fromreducefcnthat is being operated on again for further reduction. The inputs[a, b, c, ...]satisfy these properties:The inputs
[a, b, c, ...]have the same size in the first dimension.For a given index in the first dimension, every row of the blocks of data
[a, b, c, ...]either originates from the input, or originates from the same previous call toreducefcn.For a given index in the first dimension, every row of the inputs
[a, b, c, ...]for that index originates from the same index in the first dimension.
Output Arguments — All outputs
[rA, rB, rC, ...]must have the same size in the first dimension. Additionally, they must be vertically concatenable with the respective inputs[a, b, c, ...]to allow for repeated reductions when necessary.Functional Rules —
reducefcnmust satisfy these functional rules (up to roundoff error):F(input) == F(F(input)): Applying the function repeatedly to the same inputs should not change the result.F([input1; input2]) == F([input2; input1]): The result should not depend on the order of concatenation.F([input1; input2]) == F([F(input1); F(input2)]): Applying the function once to the concatenation of some intermediate results should be the same as applying it separately, concatenating, and applying it again.
Empty Inputs — Ensure that
reducefcncan handle an input that has a height of 0. Empty inputs can occur when a file is empty or if you have done a lot of filtering on the data. For this call, all input blocks are empty arrays of the correct type and size in dimensions beyond the first.
Some examples of suitable reduction functions are built-in dimension reduction
functions such as sum, prod,
max, and so on. These functions can work on intermediate results
produced by fcn and return a single scalar. These functions have the
properties that the order in which concatenations occur and the number of times the
reduction operation is applied do not change the final answer. Some functions, such as
mean and var, should generally be avoided as
reduction functions because the number of times the reduction operation is applied can
change the final answer.
Example: tC = matlab.tall.reduce(@numel,@sum,tX) finds the number
of elements in each block, and then it sums the results to count the total number of
elements.
Data Types: function_handle
Input arrays, specified as scalars, vectors, matrices, or multidimensional arrays.
The input arrays are used as inputs to the transform function fcn.
Each input array tX,tY,... must have compatible heights. Two inputs
have compatible height when they have the same height, or when one input is of height
one.
Prototype of output arrays, specified as arrays. When you specify
'OutputsLike', the output arrays tA,tB,...
returned by matlab.tall.reduce have the same data types and
attributes as the specified arrays {PA,PB,...}.
Example: tA =
matlab.tall.reduce(fcn,reducefcn,tX,'OutputsLike',{int8(1)});, where
tX is a double-precision tall array, returns tA
as int8 instead of double.
Output Arguments
Output arrays, returned as scalars, vectors, matrices, or multidimensional arrays.
If any input to matlab.tall.reduce is tall, then all output
arguments are also tall. Otherwise, all output arguments are in-memory arrays.
The size and data type of the output arrays depend on the specified functions
fcn and reducefcn. In general, the outputs
tA,tB,... must all have the same data type as the first input
tX. However, you can specify 'OutputsLike' to
return different data types. The output arrays tA,tB,... all have the
same height.
More About
When you create a tall array from a datastore, the underlying datastore
facilitates the movement of data during a calculation. The data moves in discrete pieces
called blocks or chunks, where each block is a set
of consecutive rows that can fit in memory. For example, one block of a 2-D array (such as a
table) is X(n:m,:), for some subscripts n and
m. The size of each block is based on the value of the
ReadSize property of the datastore, but the block might not be exactly
that size. For the purposes of matlab.tall.reduce, a tall array is
considered to be the vertical concatenation of many such blocks:
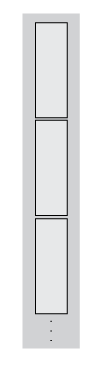
For example, if you use the sum function as the transform function,
the intermediate result is the sum per block. Therefore, instead of
returning a single scalar value for the sum of the elements, the result is a vector with
length equal to the number of
blocks.
ds = tabularTextDatastore('airlinesmall.csv','TreatAsMissing','NA'); ds.SelectedVariableNames = {'ArrDelay' 'DepDelay'}; tt = tall(ds); tX = tt.ArrDelay; f = @(x) sum(x,'omitnan'); s = matlab.tall.reduce(f, @(x) x, tX); s = gather(s)
s =
140467
101065
164355
135920
111182
186274
21321Version History
Introduced in R2018b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)