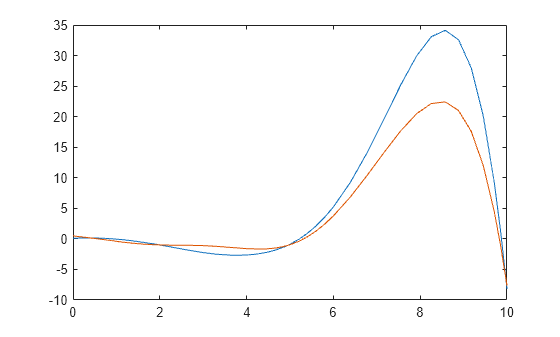
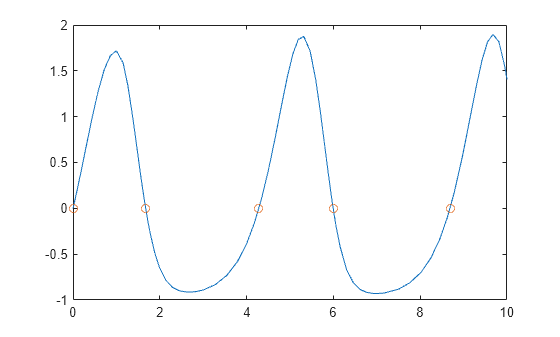
dde23
Solve delay differential equations (DDEs) with constant delays
Description
sol = dde23(ddefun,delays,history,tspan,options)options, which is a structure
created with the ddeset function. For example, use the
AbsTol and RelTol options to specify absolute and
relative error tolerances, or the Jumps option to provide locations of
discontinuities.
Examples
Input Arguments
Output Arguments
Algorithms
dde23 tracks discontinuities and integrates with the explicit
Runge-Kutta (2,3) pair and interpolant of ode23. It uses iteration to take
steps longer than the time delays.
References
[1] Shampine, Lawrence F., and S. Thompson. "Solving DDEs in MATLAB." Applied Numerical Mathematics 37, no. 4 (June 2001): 441–458. https://doi.org/10.1016/S0168-9274(00)00055-6.
[2] Kierzenka, Jacek. "Tutorial on Solving DDEs with DDE23." MATLAB Central File Exchange. Updated September 1, 2016. https://www.mathworks.com/matlabcentral/fileexchange/3899-tutorial-on-solving-ddes-with-dde23.
[3] Willé, David R., and Christopher T. H. Baker. "DELSOL—a Numerical Code for the Solution of Systems of Delay-Differential Equations." Applied Numerical Mathematics 9, no. 3 (April 1992): 223–234. https://doi.org/10.1016/0168-9274(92)90017-8.
Version History
Introduced before R2006a