colamd

Column approximate minimum degree permutation

Syntax

p = colamd(S)


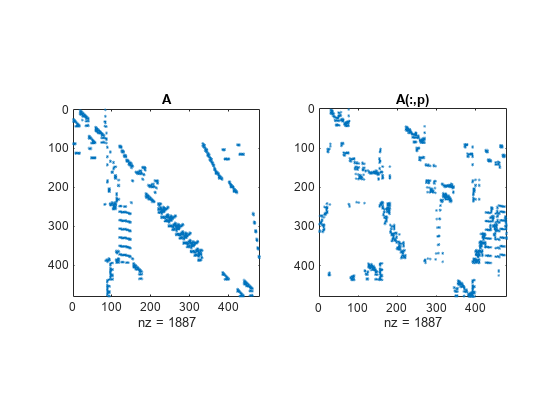
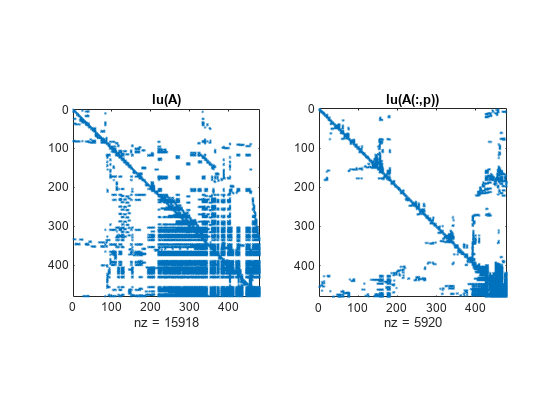
Description

p = colamd(S) returns the column approximate minimum degree permutation vector for the sparse matrix S. For a non-symmetric matrix S, S(:,p) tends to have sparser LU factors than S. The Cholesky factorization of S(:,p)' * S(:,p) also tends to be sparser than that of S'*S.

knobs is a two-element vector. If S is m-by-n, then rows with more than (knobs(1))*n entries are ignored. Columns with more than (knobs(2))*m entries are removed prior to ordering, and ordered last in the output permutation p. If the knobs parameter is not present, then knobs(1) = knobs(2) = spparms('wh_frac').

stats is an optional vector that provides data about the ordering and the validity of the matrix S.

stats(1)	Number of dense or empty rows ignored by colamd
stats(2)	Number of dense or empty columns ignored by colamd
stats(3)	Number of garbage collections performed on the internal data structure used by colamd (roughly of size 2.2*nnz(S) + 4*m + 7*n integers)
stats(4)	0 if the matrix is valid, or 1 if invalid
stats(5)	Rightmost column index that is unsorted or contains duplicate entries, or 0 if no such column exists
stats(6)	Last seen duplicate or out-of-order row index in the column index given by stats(5), or 0 if no such row index exists
stats(7)	Number of duplicate and out-of-order row indices

Although MATLAB^® built-in functions generate valid sparse matrices, a user may construct an invalid sparse matrix using the MATLAB C or Fortran APIs and pass it to colamd. For this reason, colamd verifies that S is valid:

• If a row index appears two or more times in the same column, colamd ignores the duplicate entries, continues processing, and provides information about the duplicate entries in stats(4:7).

• If row indices in a column are out of order, colamd sorts each column of its internal copy of the matrix S (but does not repair the input matrix S), continues processing, and provides information about the out-of-order entries in stats(4:7).

• If S is invalid in any other way, colamd cannot continue. It prints an error message, and returns no output arguments (p or stats) .

The ordering is followed by a column elimination tree post-ordering.

Examples

Compare Sparse Matrix and LU Factorization

The Harwell-Boeing collection of sparse matrices and the MATLAB® demos directory include a test matrix west0479. It is a matrix of order 479 resulting from a model due to Westerberg of an eight-stage chemical distillation column. The spy plot shows evidence of the eight stages. The colamd ordering scrambles this structure.

load west0479
A = west0479;
p = colamd(A);

figure()
subplot(1,2,1), spy(A,4), title('A')
subplot(1,2,2), spy(A(:,p),4), title('A(:,p)')

Comparing the spy plot of the LU factorization of the original matrix with that of the reordered matrix shows that minimum degree reduces the time and storage requirements by better than a factor of 2.8. The nonzero counts are 15918 and 5920, respectively.

figure()
subplot(1,2,1), spy(lu(A),4), title('lu(A)')
subplot(1,2,2), spy(lu(A(:,p)),4), title('lu(A(:,p))')

References

[1] Davis, Timothy A., John R. Gilbert, Stefan I. Larimore, and Esmond G. Ng. “Algorithm 836: COLAMD, a Column Approximate Minimum Degree Ordering Algorithm.” ACM Transactions on Mathematical Software 30, no. 3 (September 2004): 377–380. https://doi.org/10.1145/1024074.1024080.

Extended Capabilities

Thread-Based Environment

Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.

Version History

Introduced before R2006a