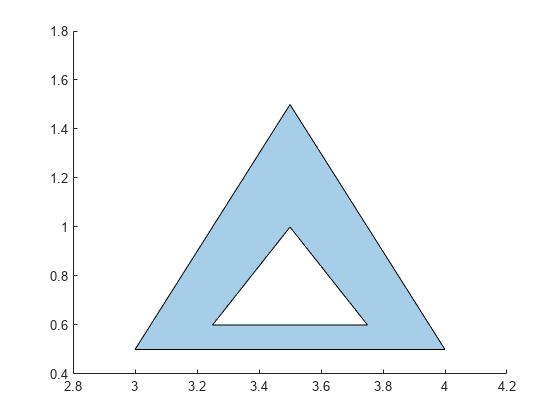boundaryshape
Create polyshape from 2-D triangulation
Description
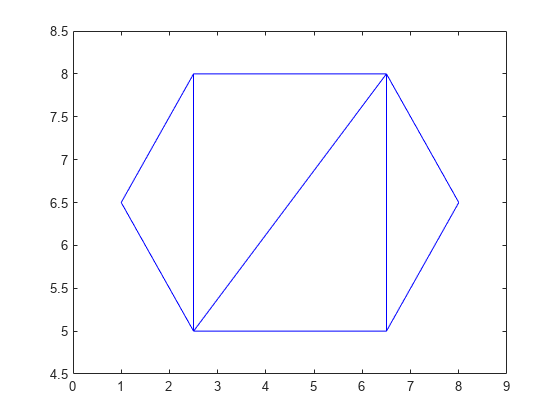
polyout = boundaryshape(TR)polyshape object from the boundary of a 2-D
triangulation. TR can be either a
triangulation object or a
delaunayTriangulation object.
Once you create the polyshape object polyout, you can analyze its
properties or perform additional computations using polyshape
functions. For example, you can access the vertices that define the boundary with
the property polyout.Vertices, and you can plot the shape using
the command plot(polyout).
Examples
Input Arguments
Output Arguments
Version History
Introduced in R2018b