smoothSurfaceMesh
Syntax
Description
surfaceMeshOut = smoothSurfaceMesh(surfaceMeshIn,numIterations)surfaceMeshIn iteratively in the specified
number of iterations numIterations.
surfaceMeshOut = smoothSurfaceMesh(surfaceMeshIn,numIterations,Name=Value)SmoothVertexColors=true smooths the vertex colors of the surface
mesh.
Examples
Define the x-, y-, and z- coordinates of the vertices.
[x,y] = meshgrid(1:15,1:15); z = peaks(15); vertices = [x(:) y(:) z(:)];
Define triangular faces for the vertices using Delaunay triangulation.
faces = delaunay(x,y);
Define a surface mesh from the vertices and faces.
surfaceMeshIn = surfaceMesh(vertices,faces);
Visualize the surface mesh.
fig = figure; v = viewer3d(fig,BackgroundColor="k",BackgroundGradient="off",Title="Original Mesh");
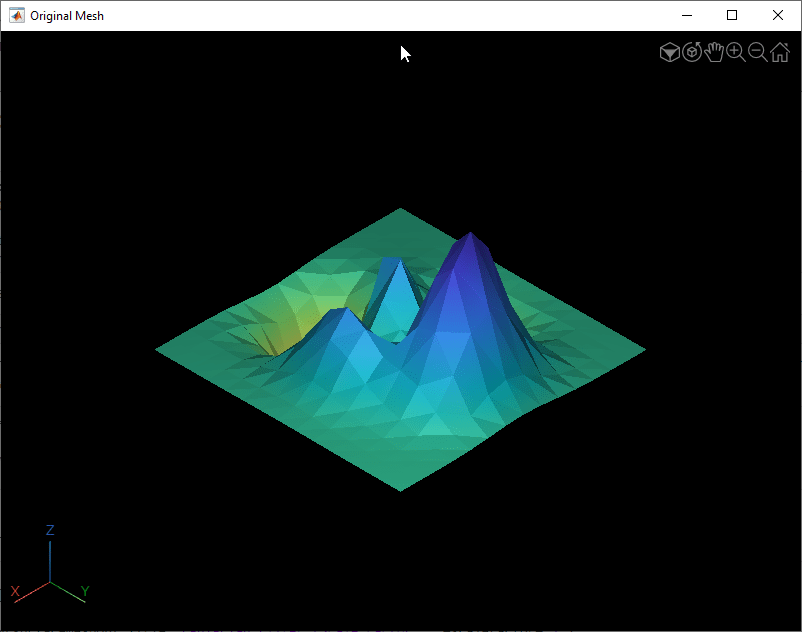
surfaceMeshShow(surfaceMeshIn,'Parent',v)Smooth Surface Mesh Using Average Filter
Smooth the surface mesh using the average filter with varying number of iterations. Visualize the smooth surface meshes. Observe that the smoothing increases with number of iterations. The mesh shrinkage also increases with number of iterations.
for numIterations = [2 5 10] surfaceMeshOut = smoothSurfaceMesh(surfaceMeshIn,numIterations); fig = figure; v = viewer3d(fig,BackgroundColor="k",BackgroundGradient="off",Title="Average Filter (Iterations = " + num2str(numIterations) + ")"); surfaceMeshShow(surfaceMeshOut,'Parent',v) end
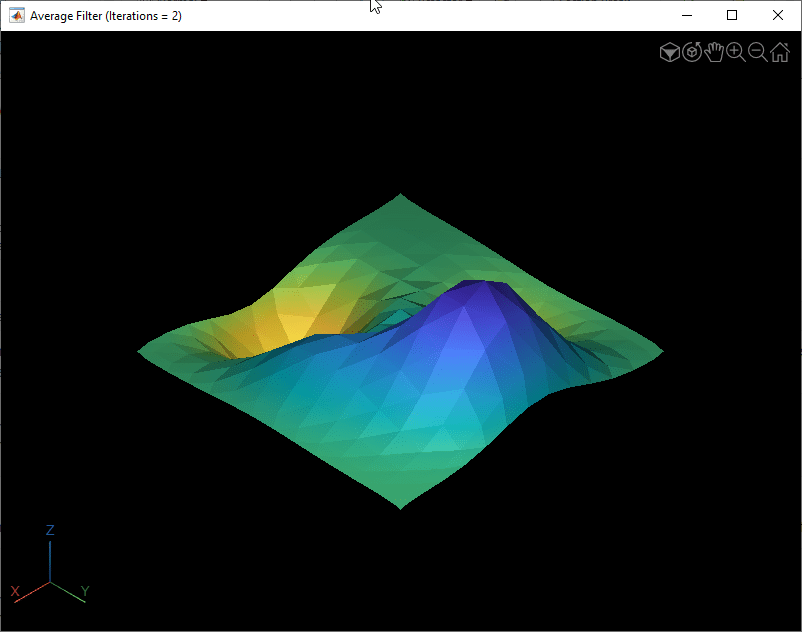
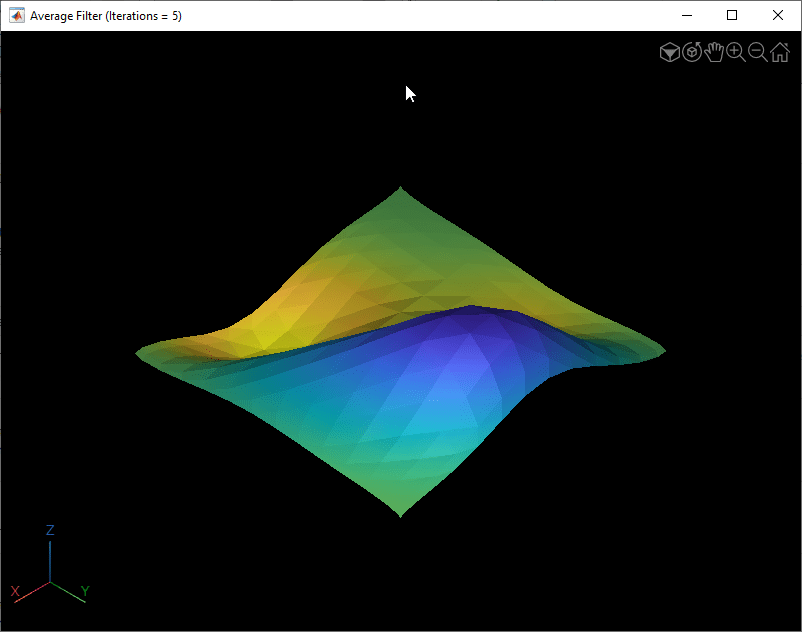

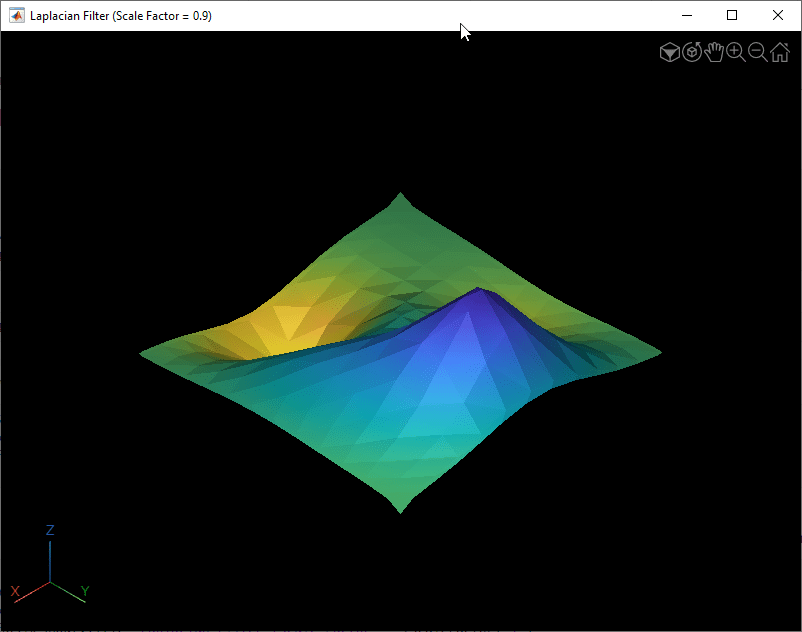
Smooth Surface Mesh Using Laplacian Filter
Smooth the surface mesh using the Laplacian filter with varying scale factor. Visualize the smooth surface meshes. Observe that the smoothing increases with the scale factor.
numIterations = 5; for scaleFactor = [0.3 0.6 0.9] surfaceMeshOut = smoothSurfaceMesh(surfaceMeshIn,numIterations,Method="Laplacian",ScaleFactor=scaleFactor); fig = figure; v = viewer3d(fig,BackgroundColor="k",BackgroundGradient="off",Title="Laplacian Filter (Scale Factor = "+scaleFactor+")"); surfaceMeshShow(surfaceMeshOut,'Parent',v) end
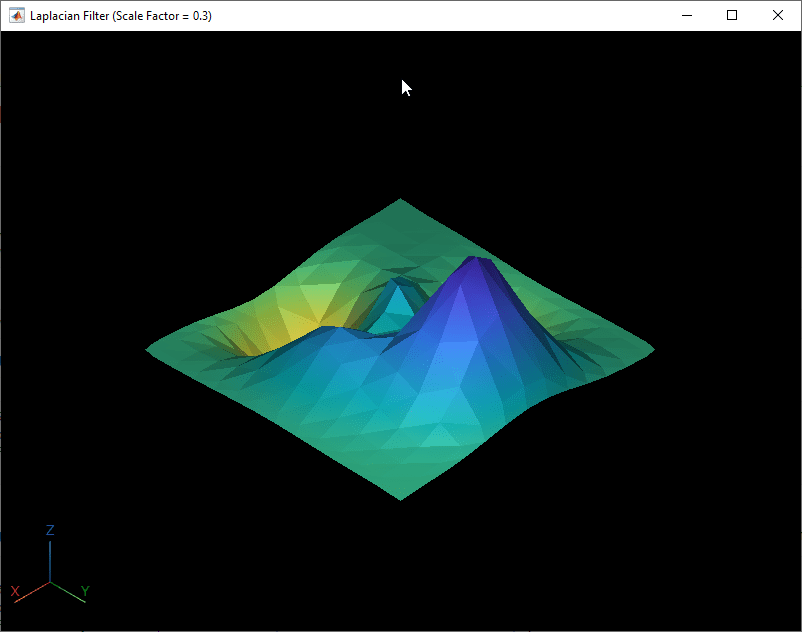

Smooth Surface Mesh Using Taubin Filter
Smooth the surface mesh using the Taubin filter. Visualize the smooth surface meshes. Observe that the mesh does not shrink even after 5 iterations.
numIterations = 5; scaleFactor = [-0.62 0.6]; surfaceMeshOut = smoothSurfaceMesh(surfaceMeshIn,numIterations,Method="Taubin",ScaleFactor=scaleFactor); fig = figure; v = viewer3d(fig,BackgroundColor="k",BackgroundGradient="off",Title="Taubin Filter");

surfaceMeshShow(surfaceMeshOut,'Parent',v)Input Arguments
Surface mesh to smooth, specified as a surfaceMesh
object.
Number of iterations, specified as a numeric scalar.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: surfaceMeshOut =
smoothSurfaceMesh(surfaceMeshIn,numIterations,Method="Laplacian") smooths the
input surface mesh using the Laplacian filter.
Method for smoothing, specified as "Average",
"Laplacian", or "Taubin".
Average filter — Repeatedly replaces each vertex in the input surface mesh with the mean average of its neighbors, including itself. The average filter is suitable for surface meshes without any sharp features.
Laplacian filter — Repeatedly moves each adjustable vertex to the weighted average of the vertices adjacent to it. The weights assigned to neighboring vertices depend on their connectivity with the adjusted vertex. The Laplacian filter is suitable for surface meshes that have various densities of vertices in different regions.
Taubin filter — Repeatedly uses two Laplacian filters with scaling factors that have different magnitudes and signs. Unlike the average and Laplacian filters, the Taubin filter prevents mesh shrinkage.
Smoothing surface meshes over multiple iterations can result in shrinkage of the original surface mesh. Thus, the average and Laplacian filters give better results across a small number of iterations. Increasing the number of iterations can result in surface mesh shrinkage for these methods. The Taubin filter prevents surface mesh shrinkage, but it requires more iterations than the average and Laplacian filters to perform a similar level of smoothing.
Data Types: char | string
Scale factor for the Laplacian and Taubin filters, specified as a numeric scalar
or two-element numeric vector. A large scale factor results in more smoothing of the
surface mesh. Specify the scale factor based on the value of the
Method name-value argument.
"Laplacian"— Specify the scale factor as a scalar in the range (0,1). The default value for the scale factor for the Laplacian filter is0.5."Taubin"— Specify the scale factor as a two-element vector, such that the two scale factors in the vector satisfy these requirements.The absolute values of the scale factors are in the range (
0,1).One scale factor is positive and the other is negative.
The absolute value of the positive scale factor is smaller than the absolute value of the negative scale factor.
To prevent surface mesh shrinkage, the difference between the absolute values of the positive and negative scale factors must be small. The default value for the scale factor for the Taubin filter is
[0.5 -0.53].
Data Types: single | double
Smooth vertex colors, specified as a logical 1
(true) or 0 (false).
Specify SmoothVertexColors as true to smooth the
vertex colors of the surface mesh.
Data Types: logical
Output Arguments
Smooth surface mesh, returned as a surfaceMesh
object with the same number of vertices and faces as
surfaceMeshIn.
Version History
Introduced in R2023a
See Also
surfaceMesh | readSurfaceMesh | writeSurfaceMesh | surfaceMeshShow | pc2surfacemesh
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)