Label and Measure Connected Components in a Binary Image
Detect Connected Components
In a binary image, a connected component, or an object, is a set of adjacent "on" pixels. Determining which pixels are adjacent depends on how pixel connectivity is defined. For a two-dimensional image, there are two standard connectivities:
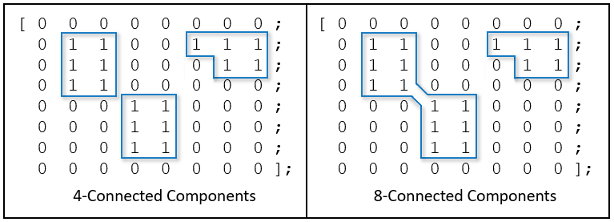
4-connectivity — Pixels are connected if their edges touch. Two adjoining pixels are part of the same object if they are both on and are connected along the horizontal or vertical direction.
8-connectivity — Pixels are connected if their edges or corners touch. Two adjoining pixels are part of the same object if they are both on and are connected along the horizontal, vertical, or diagonal direction.
You can also define nonstandard connectivity, or connectivities for higher dimensional images. For more information, see Pixel Connectivity.
This figure shows two identical matrices that represent a binary image. On each matrix is an overlay highlighting the connected components using 4-connectivity and 8-connectivity, respectively. There are three connected components using 4-connectivity, but only two connected components using 8-connectivity.
You can calculate connected components by using the bwconncomp function. In this sample
code, BW is the binary matrix shown in the above figure. For this
example, specify a connectivity of 4 so that two adjoining pixels are part of the
same object if they are both on and are connected along the horizontal or vertical
direction. The PixelIdxList field identifies the list of pixels
belonging to each connected component.
BW = zeros(8,8); BW(2:4,2:3) = 1; BW(5:7,4:5) = 1; BW(2,6:8) = 1; BW(3,7:8) = 1; BW
BW =
0 0 0 0 0 0 0 0
0 1 1 0 0 1 1 1
0 1 1 0 0 0 1 1
0 1 1 0 0 0 0 0
0 0 0 1 1 0 0 0
0 0 0 1 1 0 0 0
0 0 0 1 1 0 0 0
0 0 0 0 0 0 0 0cc4 = bwconncomp(BW,4)
cc4 =
Connectivity: 4
ImageSize: [8 8]
NumObjects: 3
PixelIdxList: {[6x1 double] [6x1 double] [5x1 double]}
For comparison, calculate the connected components of the same binary image using the default connectivity, 8.
cc8 = bwconncomp(BW)
cc8 =
Connectivity: 8
ImageSize: [8 8]
NumObjects: 2
PixelIdxList: {[12x1 double] [5x1 double]}
Label Connected Components
Labeling connected component is the process of identifying the connected components in an image and assigning each one a unique label. The resulting matrix is called a label matrix.
This figure shows the two label matrices that label the connected components using 4-connectivity and 8-connectivity, respectively.

Create a label matrix by using the labelmatrix function. This sample code continues with the connected
component structure, cc4, defined in the preceding
section.
L4 = labelmatrix(cc4)
L4 = 8×8 uint8 matrix 0 0 0 0 0 0 0 0 0 1 1 0 0 3 3 3 0 1 1 0 0 0 3 3 0 1 1 0 0 0 0 0 0 0 0 2 2 0 0 0 0 0 0 2 2 0 0 0 0 0 0 2 2 0 0 0 0 0 0 0 0 0 0 0
To visualize connected components, display the label matrix as a pseudo-color
image by using the label2rgb function. The label
identifying each object in the label matrix maps to a different color in the
associated colormap. You can specify the colormap, background color, and how objects
in the label matrix map to colors in the
colormap.
RGB_label = label2rgb(L4,@copper,"c","shuffle"); imshow(RGB_label)
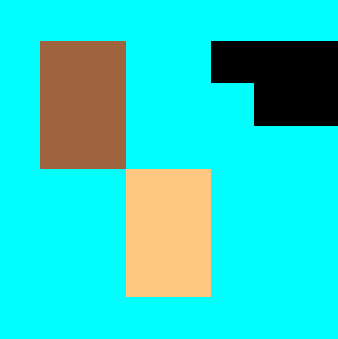
Select Objects in a Binary Image
You can use the bwselect function to select
individual objects in a binary image. Specify pixels in the input image
programmatically or interactively with a mouse. bwselect
returns a binary image that includes only those objects from the input image that
contain one of the specified pixels.
For example, use this command to select objects in the image displayed in the current axes.
BW = bwselect;
The cursor changes to cross-hairs when it is over the image. Click the objects you
want to select; bwselect displays a small star over each pixel
you click. When you are done, press Return.
bwselect returns a binary image consisting of the objects
you selected, and removes the stars.
Measure Properties of Connected Components
The regionprops and bwpropfilt functions can measure
several properties of connected components. Other functions measure a single
property. For example, the bwarea function returns the area of
a binary image.
This example uses bwarea to determine the percentage area
increase in circbw.tif that results from a dilation operation.
The area is a measure of the size of the foreground of the image and is roughly
equal to the number of on pixels in the image. However,
bwarea does not simply count the number of pixels set to
on. Rather, bwarea weights different
pixel patterns unequally when computing the area. This weighting compensates for the
distortion that is inherent in representing a continuous image with discrete pixels.
For example, a diagonal line of 50 pixels is longer than a horizontal line of 50
pixels. As a result of the weighting bwarea uses, the
horizontal line has area of 50, but the diagonal line has area of 62.5.
BW = imread("circbw.tif");
SE = ones(5);
BW2 = imdilate(BW,SE);
increase = (bwarea(BW2) - bwarea(BW))/bwarea(BW)increase =
0.3456See Also
Image Region Analyzer | bwconncomp | labelmatrix | label2rgb | bwselect | regionprops | bwpropfilt