Distance Transform of a Binary Image

The distance transform provides a metric or measure of the separation of points in the image. The bwdist function calculates the distance between each pixel that is set to off (0) and the nearest nonzero pixel for binary images.

The bwdist function supports several distance metrics.

Distance Metrics

Distance Metric	Description	Illustration
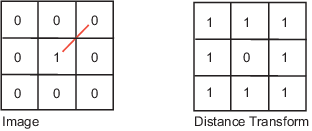
Euclidean	The Euclidean distance is the straight-line distance between two pixels.
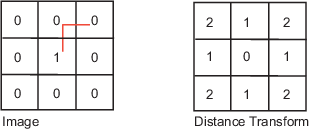
City Block	The city block distance metric measures the path between the pixels based on a 4-connected neighborhood. Pixels whose edges touch are 1 unit apart; pixels diagonally touching are 2 units apart.
Chessboard	The chessboard distance metric measures the path between the pixels based on an 8-connected neighborhood. Pixels whose edges or corners touch are 1 unit apart.
Quasi-Euclidean	The quasi-Euclidean metric measures the total Euclidean distance along a set of horizontal, vertical, and diagonal line segments.

This example creates a binary image containing two intersecting circular objects.

center1 = -10; 
center2 = -center1; 
dist = sqrt(2*(2*center1)^2); 
radius = dist/2 * 1.4; 
lims = [floor(center1-1.2*radius) ceil(center2+1.2*radius)]; 
[x,y] = meshgrid(lims(1):lims(2)); 
bw1 = sqrt((x-center1).^2 + (y-center1).^2) <= radius; 
bw2 = sqrt((x-center2).^2 + (y-center2).^2) <= radius; 
bw = bw1 | bw2; 
figure
imshow(bw)

To compute the distance transform of the complement of the binary image, use the bwdist function. In the image of the distance transform, note how the centers of the two circular areas are white.

D = bwdist(~bw); 
figure
imshow(D,[])