Recursive Polynomial Model Estimator
Estimate input-output and time-series polynomial model coefficients
Libraries:
System Identification Toolbox /
Estimators
Description
Model Structures
Use the Recursive Polynomial Model Estimator block to estimate discrete-time input-output polynomial and time-series models.
These model structures are:
AR — A(q)y(t) = e(t)
ARMA — A(q)y(t) = C(q)e(t)
ARX — A(q)y(t) = B(q)u(t – nk) + e(t)
ARMAX — A(q)y(t) = B(q)u(t – nk) + C(q)e(t)
OE —
BJ —
q is the time-shift operator and nk is the input delay. u(t) is the input, y(t) is the output, and e(t) is the error. For MISO models, there are as many B(q) polynomials as the number of inputs.
The orders of these models correspond to the maximum number of time shifts, as represented by the exponent of q. For instance, the order na is represented in the A(q) polynomial by:
1 + a1q-1 + a2q-2 + … + anaq-na.
An equivalent representation applies to the C(q), D(q), and F(q) polynomials and their corresponding orders nc, nd, and nf.
The B(q) polynomial is unique with respect to the others, because this polynomial operates on the input and contains the system zeros. For B(q), the order nb is the order of the polynomial B(q) + 1:
b1 + b2q-1 + b3q-2 + … + bnbq-(nb-1).
The orders na, nb, nc, nd, nf, and input delay nk are known ahead of time. Specify these values as block parameters. Provide u(t) and y(t) through the Inputs and Outputs inports, respectively. The block estimates the set of A(q), B(q), C(q), D(q), and F(q) coefficients that the model structure uses and outputs them in the Parameters outport. During the estimation, the block constrains the estimated C, D, and F polynomials to a stable region with roots in the unit disk, while allowing the estimated A and B polynomials to be unstable. The Parameters outport provides a bus signal with the following elements:
A — Vector containing [1 a1(t) ... ana(t)].
B — Vector containing [01 … 0nk, b1(t) ... bnb(t)]. For MISO data, B is a matrix where the i-th row parameters correspond to the i-th input.
C — Vector containing [1 c1(t) ... cnc(t)].
D — Vector containing [1 d1(t) ... dnd(t)].
F — Vector containing [1 f1(t) ... fnf(t)].
For example, suppose that you want to estimate the coefficients for the following SISO ARMAX model:
y(t) + a1y(t – 1) +...+anay(t – na) = b1u(t – nk) + … + bnbu(t – nb – nk + 1) + e(t) + c1e(t – 1) + … + cnce(t – nc)
y, u, na, nb, nc, and nk are known quantities that you provide to the block. For each time step, t, the block estimates the A, B, and C parameter values, constraining only the C polynomial to a stable region. The block then outputs these estimated values using the Parameters outport.
Block Capabilities
The block supports several estimation methods and data input formats. The block can provide both infinite-history [1] and finite-history [2] (also known as sliding-window) estimates for θ. Configurable options in the block include:
Multiple inputs (ARX model structure only) — See the Inputs port.
Sample-based or frame-based data format — See the Input Processing parameter.
Multiple infinite-history estimation methods [1] — See the Estimation Method parameter.
Infinite-history (all model structures) or finite-history (AR, ARX, or OE model structures only) — See the History parameter.
Initial conditions, enable flag, and reset trigger — See the Initial Estimate, Add enable port, and External Reset parameters.
For more information on the estimation methods, see Recursive Algorithms for Online Parameter Estimation.
Examples
Online Recursive Least Squares Estimation
Implement an online recursive least squares estimator. You estimate a nonlinear model of an internal combustion engine and use recursive least squares to detect changes in engine inertia.
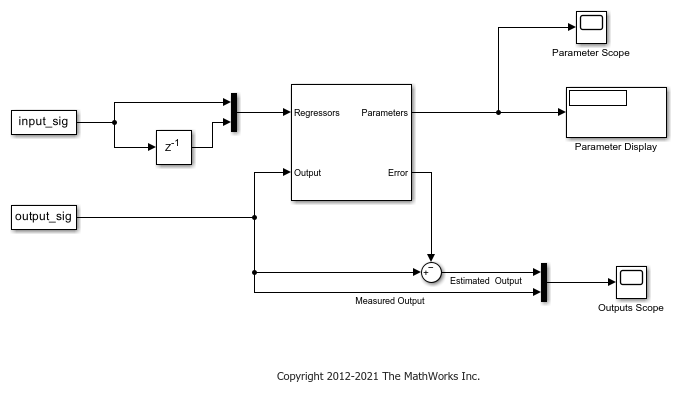
Estimate Parameters of System Using Simulink Recursive Estimator Block
Use a model containing Simulink recursive estimator to accept input and output signals, construct a regressor signal, and estimate system parameters.
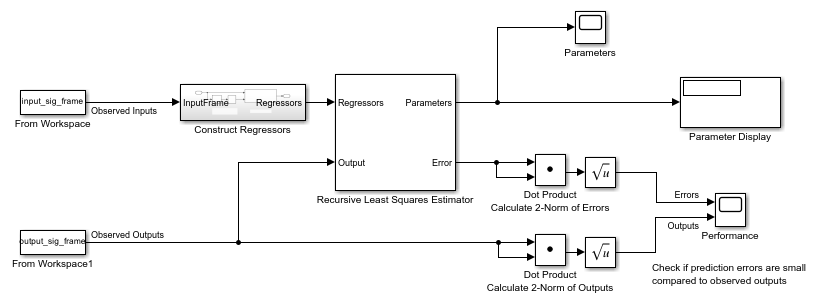
Use Frame-Based Data for Recursive Estimation in Simulink
Use frame-based signals in a Simulink recursive estimation model.
Ports
Input
Input signal u(t). The Input Processing parameter and the number of inputs nu define the dimensions of the signal. Only the ARX model structure can have multiple inputs, with nu greater than 1.
Sample-based input processing and nu inputs — nu-by-1 vector
Frame-based input processing with M samples per frame and nu inputs — M-by-nu matrix
Dependencies
To enable this port, set the Model Structure parameter to
ARX, ARMAX,
BJ, or OE.
Data Types: single | double
Measured output signal y(t). The Input Processing parameter defines the dimensions of the signal:
Sample-based input processing — Scalar
Frame-based input processing with M samples per frame — M-by-1 vector
Data Types: single | double
External signal that allows you to enable and disable estimation updates. If the signal value is:
true— Estimate and output the parameter values for the time step.false— Do not estimate the parameter values, and output the most recent previously estimated value.
Dependencies
To enable this port, select the Add enable port parameter.
Data Types: single | double | Boolean | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32
Reset parameter estimation to its initial conditions. The value of the External reset parameter determines the trigger type. The trigger type dictates whether the reset occurs on a signal that is rising, falling, either rising or falling, level, or on level hold.
Dependencies
To enable this port, select any option other than
None in the External reset
dropdown.
Data Types: single | double | Boolean | int8 | int16 | int32 | uint8 | uint16 | uint32
Initial parameter estimates, supplied from a source external to the block. The block uses this inport at the beginning of the simulation or when you trigger an algorithm reset using the Reset signal.
For information on the contents of the InitialParameters bus object, see the Parameters port description.
Dependencies
To enable this port, set History to
Infinite and Initial Estimate to
External.
Data Types: single | double
Initial parameter covariances, supplied from a source external to the block. For details, see the Parameter Covariance Matrix parameter. The block uses this inport at the beginning of the simulation or when you trigger an algorithm reset using the Reset signal.
Dependencies
To enable this port, set the following parameters:
History to
InfiniteEstimation Method to
Forgetting FactororKalman FilterInitial Estimate to
External
Data Types: single | double
Initial set of inputs when using finite-history (sliding-window) estimation, supplied from an external source.
If Model Structure is
ARX, then the signal to this port must be a (W–1+max(nb)+max(nk))-by-nu matrix, where W is the window length and nu is the number of inputs. nb is the vector of B(q) polynomial orders and nk is the vector of input delays.If Model Structure is
OE, then the signal to this port must be a (W–1+nb+nk)-by-1 vector, where W is the window length. nb is the vector of B(q) polynomial orders and nk is the vector of input delays.
The block uses this inport at the beginning of the simulation or whenever the Reset signal triggers.
If the initial buffer is set to 0 or does not contain enough
information, you see a warning message during the initial phase of your estimation.
The warning should clear after a few cycles. The number of cycles it takes for
sufficient information to be buffered depends upon the order of your polynomials and
your input delays. If the warning persists, you should evaluate the content of your
signals.
Dependencies
To enable this port, set:
History to
FiniteModel Structure to
ARXorOEInitial Estimate to
External
Data Types: single | double
Initial set of output measurements when using finite-history (sliding-window) estimation, supplied from an external source.
If Model Structure is
ARorARX, then the signal to this port must be a (W+na)-by-1 vector, where W is the window length and na is the polynomial order of A(q).If Model Structure is
OE, then the signal to this port must be a (W+nf)-by-1 vector, where W is the window length and nf is the polynomial order of F(q).
The block uses this inport at the beginning of the simulation or whenever the Reset signal triggers.
If the initial buffer is set to 0 or does not contain enough
information, you see a warning message during the initial phase of your estimation.
The warning should clear after a few cycles. The number of cycles it takes for
sufficient information to be buffered depends upon the order of your polynomials and
your input delays. If the warning persists, you should evaluate the content of your
signals.
Dependencies
To enable this port, set:
History to
FiniteModel Structure to
AR,ARX, orOEInitial Estimate to
External
Data Types: single | double
Output
Estimated polynomial coefficients, returned as a bus. The bus contains an element for each of the A, B, C, D, and F polynomials that correspond to the structure that you specify in Model Structure (see Model Structures ).
Each bus element is a vector signal containing the associated polynomial coefficients. For example, the A element contains [1 a1(t) ... ana(t)].
Estimated C, D, and F values are constrained to be stable discrete-time polynomials. That is, these polynomials all have roots within the unit circle. Estimated A and B polynomials are allowed to be unstable.
Data Types: single | double
Estimation error, returned as:
Scalar — Sample-based input processing
M-by-1 vector — Frame-based input processing with M samples per frame
Dependencies
To enable this port, select the Output estimation error parameter.
Data Types: single | double
Parameter estimation error covariance P, returned as an N-by-N matrix, where N is the number of parameters. For details, see the Output Parameter Covariance Matrix parameter.
Dependencies
To enable this port:
Select the Output parameter covariance matrix parameter.
If History is
Infinite, set Estimation Method toForgetting FactororKalman Filter.
Data Types: single | double
Parameters
Model Structure
Estimated model structure, specified as one of the following:
ARX— SISO or MISO ARX modelARMAX— SISO ARMAX modelOE— SISO OE modelBJ— SISO BJ modelAR— Time-series AR modelARMA— Time-series ARMA model
Model Parameters
Specify how to provide initial parameter estimates to the block:
None— Do not specify initial estimates.The block uses
0as the initial parameter estimate.Specify the parameters that the block enables based on your choice of model structure and estimation method.
Specify the set of Number of Parameters () parameters that the block enables based on your Model Structure. For instance, if your setting for Model Structure is
AR, specify the Number of Parameters in A(q) (na) parameter.Specify the Input Delay (nk) parameter that the block enables when your model structure uses a B(q) element.
Specify the Parameter Covariance Matrix if Estimation Method is
Forgetting FactororKalman Filter.
Internal— Specify initial parameter estimates internally to the block.Specify the initial parameter values Initial () parameters that the block enables based on your Model Structure and History. For instance, if your setting for Model Structure is
ARand History isInfinite, specify the Initial A(q) parameter.Specify the Input Delay (nk) parameter that the block enables when your model structure uses a B(q) element.
Specify the Parameter Covariance Matrix parameter if Estimation Method is
Forgetting FactororKalman Filter.Specify the Initial Inputs parameter (
ARXandOEonly) and the Initial Outputs parameter (ARX,AR, andOE) if History isFinite.
External— Specify initial parameter estimates as an input signal to the block.Specify the Number of Parameters () parameters that the block enables based on your Model Structure. Your setting for Model Structure and for the History parameter determines which signals to connect to the relevant ports:
If History is
Infinite— InitialParameters and InitialCovarianceIf History is
Finite— InitialOutputs for theAR,ARX, andOEmodel structures, and InitialInputs for theARXandOEmodel structures
Programmatic Use
Block Parameter:
InitialEstimateSource |
| Type: character vector, string |
Values: 'None',
'Internal', 'External' |
Default: 'None' |
Specify the number of estimated parameters na in the A(q) polynomial.
Dependencies
To enable this parameter, either:
Set History to
Infinite, Model Structure toAR,ARX,ARMA, orARMAX, and Initial Estimate toNoneorExternal.Set History to
Finite, Model Structure toARorARX, and Initial Estimate toNoneorExternal.
Programmatic Use
Block Parameter:
A0 |
| Type: non-negative integer |
Default: 1 |
Specify the number of estimated parameters nb in the B(q) polynomial.
For MISO systems using an ARX model structure, specify nb as a
vector with as many elements as there are inputs. Each element of this vector
represents the order of the B(q) polynomial
associated with the corresponding input. For example, suppose that you have a
two-input MISO system whose B(q) elements are: . The zero at the beginning of each polynomial represents a single
input delay for each input (see the Initial B(q) parameter
description). The trailing zero in B1 is for
equalizing the length of the polynomials and has no impact on estimation.
nb for each polynomial is equal to the number of estimated
parameters following the initial zero, or 1 for input 1 and 2 for input 2. Specify
Number of Parameters in B(q) (nb) as [1 2],
and Input Delay (nk) as [1 1].
Dependencies
To enable this parameter, either:
Set History to
Infinite, Model Structure toARX,ARMAX,BJ, orOE, and Initial Estimate toNoneorExternal.Set History to
Finitewith Model Structure ofARXorOEand Initial Estimate toNoneorExternal.
Programmatic Use
Block Parameter:
B0 |
| Type: positive integer |
Default: 1 |
Specify the number of estimated parameters nc in the C(q) polynomial.
Dependencies
To enable this parameter, set History to
Infinite, Model Structure to
ARMA, ARMAX, or
BJ, and Initial Estimate to
None or External
Programmatic Use
Block Parameter:
C0 |
| Type: positive integer |
Default: 1 |
Specify the number of estimated parameters nd in the D(q) polynomial.
Dependencies
To enable this parameter, set History to
Infinite, Model Structure to
BJ, and Initial Estimate to
None or External.
Programmatic Use
Block Parameter:
D0 |
| Type: positive integer |
Default: 1 |
Specify the number of estimated parameters nf in the F(q) polynomial.
Dependencies
To enable this parameter, set Initial Estimate to
None or External and
either:
History to
Infinite, Model Structure toOEorBJ, and Initial Estimate toNoneorExternalHistory to
Finite, Model Structure toOE, and Initial Estimate toNoneorExternal
.
Programmatic Use
Block Parameter:
F0 |
| Type: positive integer |
Default: 1 |
Specify the input delay as an integer representing the number of time steps that occur before the input affects the output. This delay is also called the dead time in the system. The block encodes the input delay as fixed leading zeros of the B(q) polynomial. For more information, see the B(q) parameter description.
For MISO systems with ARX model structure, specify nk as a vector with elements specifying the delay for each input. This vector is of length nu, where nu is the number of inputs.
For example, suppose that you have a two-input MISO system whose
B(q) elements are: . The zeros at the beginning of the polynomials represent a
single-sample delay for the first input, and a two-sample delay for the second input
(see the Initial B(q) parameter description).
nb for each polynomial is equal to the number of estimated
parameters following the initial zeros, or 2 for input 1 and 1 for input 2. Specify
Input Delay (nk) as [1 2], and
Number of Parameters in B(q) (nb) as [2
1].
Dependencies
To enable this parameter, either:
Set History to
Infinite, Model Structure toARX,ARMAX,OE, orBJ, and Initial Estimate toNoneorExternal.Set History to
Finite, Model Structure toARXorOE, and Initial Estimate toNoneorExternal.
Programmatic Use
Block Parameter:
nk |
| Type: non-negative integer vector |
Default: 1 |
Real positive scalar, α — Covariance matrix is an N-by-N diagonal matrix, with α as the diagonal elements.
Vector of real positive scalars, [α(a),α(b),α(c), α(d), α(f)] — Covariance matrix is an N-by-N diagonal matrix, with [α(a),α(b),α(c),α(d), α(f)] as the diagonal elements. α(a) is a vector of the covariance for each coefficient of the A polynomial. Similarly, α(b), α(c), α(d) and α(f) are vectors containing the covariance of the coefficients of the B, C, D and F polynomials, respectively.
N-by-N symmetric positive-definite matrix.
N can be one of the following:
AR— N = naARX—ARMA— N = na + ncARMAX— N = na + nb + ncOE— N = nb + nfBJ— N = nb + nc + nd + nf
Dependencies
To enable this parameter, set
History to
InfiniteInitial Estimate to
NoneorInternalEstimation Method to
Forgetting FactororKalman Filter
The block uses this parameter at the beginning of the simulation or whenever the Reset signal triggers.
Programmatic Use
Block Parameter:
P0 |
| Type: scalar, vector, or matrix |
Default: 1e4 |
Specify the initial estimate of the A(q) polynomial coefficients as a row vector of length na+1.
The leading coefficient of A must be
1.
Dependencies
To enable this parameter, set:
Model Structure to
AR,ARX,ARMA, orARMAXInitial Estimate to
Internal
Programmatic Use
Block Parameter:
A0 |
| Type: real vector |
Default: [1
eps] |
Specify the initial estimate of the B(q) polynomial coefficients as a row vector of length nb+nk. For multiple-input models, specify a matrix where the ith row corresponds to the ith input.
The block counts the leading zeros in B(q) and interprets them as input delay nk. Those zeros are fixed throughout the estimation. nb is the number of elements after the first nonzero element in B(q). The block estimates the value of these nb elements.
For example:
[0 eps]corresponds to nk=1 and nb=1.[0 0 eps]corresponds to nk=2 and nb=1.[0 0 eps 0 eps]corresponds to nk=2 and nb=3.
The default value is [0 eps].
Dependencies
To enable this parameter, set:
Model Structure to
ARX,ARMAX,OE, orBJInitial Estimate to
Internal
Programmatic Use
Block Parameter:
B0 |
| Type: real vector or matrix |
Default: [0
eps] |
Specify the initial estimate of the C(q) polynomial coefficients as a row vector of length nc+1.
The leading coefficient of C(q) must be 1.
The coefficients must define a stable discrete-time polynomial, that is, have all polynomial roots within the unit circle.
Dependencies
To enable this parameter, set:
History to
InfiniteModel Structure to
ARMA,ARMAX, orBJInitial Estimate to
Internal
Programmatic Use
Block Parameter:
C0 |
| Type: real vector |
Default: [1
eps] |
Specify the initial estimate of the D(q) polynomial coefficients as a row vector of length nd+1.
The leading coefficient of D(q) must be 1.
The coefficients must define a stable discrete-time polynomial, that is, have all polynomial roots within the unit circle.
Dependencies
To enable this parameter, set:
History to
InfiniteModel Structure to
BJInitial Estimate to
Internal
Programmatic Use
Block Parameter:
D0 |
| Type: real vector |
Default: [1
eps] |
Specify the initial estimate of the F(q) polynomial coefficients as a row vector of length nf+1.
The leading coefficient of F(q) must be 1.
The coefficients must define a stable discrete-time polynomial, that is, have all polynomial roots within the unit circle.
Dependencies
To enable this parameter, set:
Model Structure to
OEor toBJInitial Estimate to
Internal
Programmatic Use
Block Parameter:
F0 |
| Type: real vector |
Default: [1
eps] |
Specify initial values of the inputs buffer when using finite-history (sliding window) estimation. The buffer dimensions accommodate the specified window length, the regressors associated with polynomials within that window, the input delays, and the number of inputs. These elements drive a matrix size of:
ARX model structure — (W–1+max(nb)+max(nk))-by-nu
OE model structure — (W–1+nb+nk)-by-1
where W is the window length and nu is the number of inputs. nb is the vector of B(q) polynomial orders and nk is the vector of input delays.
When the initial value is set to 0, the block populates the
buffer with zeros.
If the initial buffer is set to 0 or does not contain enough
information, you see a warning message during the initial phase of your estimation.
The warning should clear after a few cycles. The number of cycles it takes for
sufficient information to be buffered depends upon the order of your polynomials and
your input delays. If the warning persists, you should evaluate the content of your
signals.
The block uses this parameter at the beginning of the simulation or whenever the Reset signal triggers.
Dependencies
To enable this parameter, set
History to
FiniteModel Structure to
ARXorOEInitial Estimate to
Internal
.
Programmatic Use
Block Parameter:
InitialInputs |
| Type: real matrix |
Default: 0 |
Specify initial values of the measured outputs buffer when using finite-history (sliding-window) estimation. The buffer dimensions accommodate the specified window length and the regressors associated with the polynomials within that window.
AR or ARX model structure — (W+na)-by-1 vector, where W is the window length and na is the polynomial order of A(q).
OE model structure — (W+nf)-by-1 vector, where W is the window length and nf is the polynomial order of F(q).
When the initial value is set to 0, the block populates the
buffer with zeros.
If the initial buffer is set to 0 or does not contain enough
information, you see a warning message during the initial phase of your estimation.
The warning should clear after a few cycles. The number of cycles it takes for
sufficient information to be buffered depends upon the order of your polynomials and
your input delays. If the warning persists, you should evaluate the content of your
signals.
The block uses this parameter at the beginning of the simulation or whenever the Reset signal triggers.
Dependencies
To enable this parameter, set:
History to
FiniteModel Structure to
AR,ARX, orOEInitial Estimate to
Internal
Programmatic Use
Block Parameter:
InitialOutputs |
| Type: real vector |
Default: 0 |
Input Processing and Sample Time
Sample-basedprocessing operates on signals streamed one sample at a time.Frame-basedprocessing operates on signals containing samples from multiple time steps. Many machine sensor interfaces package multiple samples and transmit these samples together in frames.Frame-basedprocessing allows you to input this data directly without having to first unpack it.
Specifying frame-based data adds an extra dimension of M to some of your data inports and outports, where M is the number of time steps in a frame. These ports are:
Inputs
Output
Error
For more information, see the port descriptions in Ports.
Programmatic Use
Block Parameter:
InputProcessing |
| Type: character vector, string |
Values: 'Sample-based',
'Frame-based' |
Default:
'Sample-based' |
Specify the data sample time, whether by individual samples for sample-based processing (ts), or by frames for frame-based processing (tf = Mts), where M is the frame length. When you set Sample Time to its default value of –1, the block inherits its ts or tf based on the signal.
Specify Sample Time as a positive scalar to override the inheritance.
Programmatic Use
Block Parameter:
Ts |
| Type: real scalar |
Values: –1, positive
scalar |
Default: –1 |
Algorithm and Block Options
Algorithm Options
The History parameter determines what type of recursive algorithm you use:
Infinite— Algorithms in this category aim to produce parameter estimates that explain all data since the start of the simulation. These algorithms retain the history in a data summary. The block maintains this summary within a fixed amount of memory that does not grow over time.The block provides multiple algorithms of the
Infinitetype. Selecting this option enables the Estimation Method parameter with which you specify the algorithm.Finite— Algorithms in this category aim to produce parameter estimates that explain only a finite number of past data samples. The block uses all of the data within a finite window, and discards data once that data is no longer within the window bounds. This method is also called sliding-window estimation.The block provides one algorithm of the
Finitetype. You can use this option only with theAR,ARX, andOEmodel structures.Selecting this option enables the Window Length parameter.
For more information on recursive estimation methods, see Recursive Algorithms for Online Parameter Estimation.
Programmatic Use
Block Parameter:
History |
| Type: character vector, string |
Values: 'Infinite',
'Finite' |
Default:
'Infinite' |
The Window Length parameter determines the number of time samples to use for the finite-history (sliding-window) estimation method. Choose a window size that balances estimation performance with computational and memory burden. Sizing factors include the number and time variance of the parameters in your model. Always specify Window Length in samples, even if you are using frame-based input processing.
Window Length must be greater than or equal to the number of estimated parameters.
Suitable window length is independent of whether you are using sample-based or frame-based input processing. However, when using frame-based processing, Window Length must be greater than or equal to the number of samples (time steps) contained in the frame.
Dependencies
To enable this parameter, set History to
Finite.
Programmatic Use
Block Parameter:
WindowLength |
| Type: positive integer |
Default: 200 |
Specify the estimation algorithm when performing infinite-history estimation. When you select any of these methods, the block enables additional related parameters.
Forgetting factor and Kalman filter algorithms are more computationally intensive than gradient and normalized gradient methods. However, these more intensive methods have better convergence properties than the gradient methods. For more information about these algorithms, see Recursive Algorithms for Online Parameter Estimation.
Programmatic Use
Block Parameter:
EstimationMethod |
| Type: character vector, string |
Values: 'Forgetting
Factor','Kalman Filter','Normalized
Gradient','Gradient' |
Default: 'Forgetting
Factor' |
The forgetting factor λ specifies if and how much old data is discounted in the estimation. Suppose that the system remains approximately constant over T0 samples. You can choose λ such that:
Setting λ = 1 corresponds to “no forgetting” and estimating constant coefficients.
Setting λ < 1 implies that past measurements are less significant for parameter estimation and can be “forgotten.” Set λ < 1 to estimate time-varying coefficients.
Typical choices of λ are in the [0.98 0.995] range.
Dependencies
To enable this parameter, set History to
Infinite and Estimation Method to
Forgetting Factor.
Programmatic Use
Block Parameter:
AdaptationParameter |
| Type: scalar |
| Values: (0 1] range |
Default: 1 |
Process Noise Covariance prescribes the elements and structure of the noise covariance matrix for the Kalman filter estimation. Using N as the number of parameters to estimate, specify the Process Noise Covariance as one of the following:
Real nonnegative scalar, α — Covariance matrix is an N-by-N diagonal matrix, with α as the diagonal elements.
Vector of real nonnegative scalars, [α1,...,αN] — Covariance matrix is an N-by-N diagonal matrix, with [α1,...,αN] as the diagonal elements.
N-by-N symmetric positive semidefinite matrix.
The Kalman filter algorithm treats the parameters as states of a dynamic system and estimates these parameters using a Kalman filter. Process Noise Covariance is the covariance of the process noise acting on these parameters. Zero values in the noise covariance matrix correspond to constant coefficients, or parameters. Values larger than 0 correspond to time-varying parameters. Use large values for rapidly changing parameters. However, expect the larger values to result in noisier parameter estimates. The default value is 1.
Dependencies
To enable this parameter, set History to
Infinite and Estimation Method to
Kalman Filter.
Programmatic Use
Block Parameter:
AdaptationParameter |
| Type: scalar, vector, matrix |
Default: 1 |
The adaptation gain γ scales the influence of new measurement data on the estimation results for the gradient and normalized gradient methods. When your measurements are trustworthy, or in other words have a high signal-to-noise ratio, specify a larger value for γ. However, setting γ too high can cause the parameter estimates to diverge. This divergence is possible even if the measurements are noise free.
When Estimation Method is
NormalizedGradient, Adaptation Gain
should be less than 2. With either gradient method, if errors are growing in time (in
other words, estimation is diverging), or parameter estimates are jumping around
frequently, consider reducing Adaptation Gain.
Dependencies
To enable this parameter, set History to
Infinite and Estimation Method to
Normalized Gradient or to
Gradient.
Programmatic Use
Block Parameter:
AdaptationParameter |
| Type: scalar |
Default: 1 |
The normalized gradient algorithm scales the adaptation gain at each step by the square of the two-norm of the gradient vector. If the gradient is close to zero, the near-zero denominator can cause jumps in the estimated parameters. Normalization Bias is the term introduced to the denominator to prevent these jumps. Increase Normalization Bias if you observe jumps in estimated parameters.
Dependencies
To enable this parameter, set History to
Infinite and Estimation Method to
Normalized Gradient.
Programmatic Use
Block Parameter:
NormalizationBias |
| Type: scalar |
Default: eps |
Block Options
Use the Error outport signal to validate the estimation. For a given time step t, the estimation error e(t) is calculated as:
where y(t) is the measured output that you provide, and yest(t) is the estimated output using the regressors H(t) and parameter estimates θ(t-1).
Programmatic Use
Block Parameter:
OutputError |
| Type: character vector, string |
Values:
'off','on', |
Default: 'off' |
Use the Covariance outport signal to examine parameter
estimation uncertainty. The software computes parameter covariance
P assuming that the residuals,
e(t), are white noise, and the variance of
these residuals is 1.
The interpretation of P depends on the estimation approach you
specify in History and Estimation Method as follows:
If History is
Infinite, then your Estimation Method selection results in:Forgetting Factor— (R2/2)Pis approximately equal to the covariance matrix of the estimated parameters, where R2 is the true variance of the residuals. The block returns these residuals through the Error port.Kalman Filter— R2Pis the covariance matrix of the estimated parameters, and R1 /R2 is the covariance matrix of the parameter changes. Here, R1 is the covariance matrix that you specify in Parameter Covariance Matrix.Normalized GradientorGradient— CovariancePis not available.
If History is
Finite(sliding-window estimation) — R2Pis the covariance of the estimated parameters. The sliding-window algorithm does not use this covariance in the parameter-estimation process. However, the algorithm does compute the covariance for output so that you can use it for statistical evaluation.
Programmatic Use
Block Parameter:
OutputP |
| Type: character vector, string |
Values:
'off','on' |
Default: 'off' |
Use the Enable signal to provide a control signal that enables or disables parameter estimation. The block estimates the parameter values for each time step that parameter estimation is enabled. If you disable parameter estimation at a given step, t, then the software does not update the parameters for that time step. Instead, the block output contains the last estimated parameter values.
You can use this option, for example, when or if:
Your regressors or output signal become too noisy, or do not contain information at some time steps
Your system enters a mode where the parameter values do not change in time
Programmatic Use
Block Parameter:
AddEnablePort |
| Type: character vector, string |
Values:
'off','on' |
Default: 'off' |
Set the External reset parameter to both add a Reset inport and specify the inport signal condition that triggers a reset of algorithm states to their specified initial values. Reset the estimation, for example, if parameter covariance is becoming too large because of lack of either sufficient excitation or information in the measured signals. The External reset parameter determines the timing for the reset.
Suppose that you reset the block at a time step, t. If the block is enabled at t, the software uses the initial parameter values specified in Initial Estimate to estimate the parameter values. In other words, at t, the block performs a parameter update using the initial estimate and the current values of the inports.
If the block is disabled at t and you reset the block, the block output contains the values specified in Initial Estimate.
Specify this option as one of the following:
None— Algorithm states and estimated parameters are not reset.Rising— Trigger reset when the control signal rises from a negative or zero value to a positive value. If the initial value is negative, rising to zero triggers reset.Falling— Trigger reset when the control signal falls from a positive or a zero value to a negative value. If the initial value is positive, falling to zero triggers reset.Either— Trigger reset when the control signal is either rising or falling.Level— Trigger reset in either of these cases:Control signal is nonzero at the current time step.
Control signal changes from nonzero at the previous time step to zero at the current time step.
Level hold— Trigger reset when the control signal is nonzero at the current time step.
When you choose any option other than None, the
software adds a Reset inport to the block. You provide the reset control input signal
to this inport.
Programmatic Use
Block Parameter:
ExternalReset |
| Type: character vector, string |
Values:
'None','Rising','Falling',
'Either', 'Level', 'Level
hold' |
Default: 'None' |
References
[1] Ljung, L. System Identification: Theory for the User. Upper Saddle River, NJ: Prentice-Hall PTR, 1999, pp. 363–369.
[2] Zhang, Q. "Some Implementation Aspects of Sliding Window Least Squares Algorithms." IFAC Proceedings. Vol. 33, Issue 15, 2000, pp. 763–768.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
PLC Code Generation
Generate Structured Text code using Simulink® PLC Coder™.
Version History
Introduced in R2014a
See Also
Recursive Least Squares Estimator | Kalman Filter
Topics
- Estimate Parameters of System Using Simulink Recursive Estimator Block
- Online Recursive Least Squares Estimation
- Preprocess Online Parameter Estimation Data in Simulink
- Validate Online Parameter Estimation Results in Simulink
- Generate Online Parameter Estimation Code in Simulink
- Recursive Algorithms for Online Parameter Estimation
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)