surrogateopt

Surrogate optimization for global minimization of time-consuming objective functions

Syntax

x = surrogateopt(objconstr,lb,ub)

x = surrogateopt(objconstr,lb,ub,intcon)

x = surrogateopt(objconstr,lb,ub,intcon,A,b,Aeq,beq)

x = surrogateopt(___,options)

x = surrogateopt(problem)

x = surrogateopt(checkpointFile)

x = surrogateopt(checkpointFile,opts)

[x,fval] = surrogateopt(___)

[x,fval,exitflag,output] = surrogateopt(___)

[x,fval,exitflag,output,trials] = surrogateopt(___)

Description

surrogateopt is a global solver for time-consuming objective functions.

surrogateopt attempts to solve problems of the form

$$\underset{x}{\min }f(x)\text{ such that }\{\begin{array}{l}\text{lb}\le x\le \text{ub}\\ A·x\le b\\ \text{Aeq}·x=\text{beq}\\ c(x)\le 0\\ x_i\text{ integer, }i\in \text{intcon}\text{.}\end{array}$$

The solver searches for the global minimum of a real-valued objective function in multiple dimensions, subject to bounds, optional linear constraints, optional integer constraints, and optional nonlinear inequality constraints. surrogateopt is best suited to objective functions that take a long time to evaluate. The objective function can be nonsmooth. The solver requires finite bounds on all variables. The solver can optionally maintain a checkpoint file to enable recovery from crashes or partial execution, or optimization continuation after meeting a stopping condition. The objective function f(x) can be empty ([]), in which case surrogateopt attempts to find a point satisfying all the constraints.

x = surrogateopt(objconstr,lb,ub) searches for a global minimum of objconstr(x) in the region lb <= x <= ub. If objconstr(x) returns a structure, then surrogateopt searches for a minimum of objconstr(x).Fval, subject to objconstr(x).Ineq <= 0.

Note

Passing Extra Parameters explains how to pass extra parameters to the objective function, if necessary.

x = surrogateopt(objconstr,lb,ub,intcon) requires that the variables listed in intcon take integer values.

x = surrogateopt(objconstr,lb,ub,intcon,A,b,Aeq,beq) requires that the solution x satisfy the inequalities A*x <= b and the equalities Aeq*x = beq. If no inequalities exist, set A = [] and b = []. Similarly, if no equalities exist, set Aeq = [] and beq = [].

x = surrogateopt(___,options) modifies the search procedure using the options in options. Specify options following any input argument combination in the previous syntaxes.

x = surrogateopt(problem) searches for a minimum for problem, a structure described in problem.

x = surrogateopt(checkpointFile) continues running the optimization from the state in a saved checkpoint file. See Work with Checkpoint Files.

x = surrogateopt(checkpointFile,opts) continues running the optimization from the state in a saved checkpoint file, and replaces options in checkpointFile with those in opts. See Checkpoint File.

[x,fval] = surrogateopt(___) also returns the best (smallest) value of the objective function found by the solver, using any of the input argument combinations in the previous syntaxes.

[x,fval,exitflag,output] = surrogateopt(___) also returns exitflag, an integer describing the reason the solver stopped, and output, a structure describing the optimization procedure.

[x,fval,exitflag,output,trials] = surrogateopt(___) also returns a structure containing all of the evaluated points and the objective function values at those points.

Examples

Search for Global Minimum

Search for a minimum of the six-hump camel back function in the region -2.1 <= x(i) <= 2.1. This function has two global minima with the objective function value -1.0316284... and four local minima with higher objective function values.

rng default % For reproducibility
objconstr = @(x)(4*x(:,1).^2 - 2.1*x(:,1).^4 + x(:,1).^6/3 ...
    + x(:,1).*x(:,2) - 4*x(:,2).^2 + 4*x(:,2).^4);
lb = [-2.1,-2.1];
ub = -lb;
x = surrogateopt(objconstr,lb,ub)

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

x = 1×2

    0.0895   -0.7130

Solve Problem with Nonlinear Constraints

Find the minimum of Rosenbrock's function

$$100(x(2)-x(1{)}^2{)}^2+(1-x(1){)}^2$$

subject to the nonlinear constraint that the solution lies in a disk of radius 1/3 around the point [1/3,1/3]:

$$(x(1)-1/3{)}^2+(x(2)-1/3{)}^2\le (1/3{)}^2$$.

To do so, write a function objconstr(x) that returns the value of Rosenbrock's function in a structure field Fval, and returns the nonlinear constraint value in the form $$c(x)\le 0$$ in the structure field Ineq.

type objconstr

function f = objconstr(x)
f.Fval = 100*(x(2) - x(1)^2)^2 + (1 - x(1))^2;
f.Ineq = (x(1)-1/3)^2 + (x(2)-1/3)^2 - (1/3)^2;

Call surrogateopt using lower bounds of 0 and upper bounds of 2/3 on each component.

lb = [0,0];
ub = [2/3,2/3];
[x,fval,exitflag] = surrogateopt(@objconstr,lb,ub)

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

x = 1×2

    0.6541    0.4279

fval = 0.1197

exitflag = 0

Check the value of the nonlinear constraint at the solution.

disp(objconstr(x).Ineq)

   7.0843e-04

The constraint function value is near zero, indicating that the constraint is active at the solution.

Solve Mixed-Integer Problem

Find the minimum of the ps_example function for a two-dimensional variable x whose first component is restricted to integer values, and all components are between –5 and 5.

intcon = 1;
rng default % For reproducibility
objconstr = @ps_example;
lb = [-5,-5];
ub = [5,5];
x = surrogateopt(objconstr,lb,ub,intcon)

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

x = 1×2

   -5.0000    0.0001

Surrogate Optimization Using Nondefault Options

Minimize the six-hump camel back function in the region -2.1 <= x(i) <= 2.1. This function has two global minima with the objective function value -1.0316284... and four local minima with higher objective function values.

To search the region systematically, use a regular grid of starting points. Set 120 as the maximum number of function evaluations. Use the 'surrogateoptplot' plot function. To understand the 'surrogateoptplot' plot, see Interpret surrogateoptplot.

rng default % For reproducibility
objconstr = @(x)(4*x(:,1).^2 - 2.1*x(:,1).^4 + x(:,1).^6/3 ...
    + x(:,1).*x(:,2) - 4*x(:,2).^2 + 4*x(:,2).^4);
lb = [-2.1,-2.1];
ub = -lb;
[Xpts,Ypts] = meshgrid(-3:3);
startpts = [Xpts(:),Ypts(:)];
options = optimoptions('surrogateopt','PlotFcn','surrogateoptplot',...
    'InitialPoints',startpts,'MaxFunctionEvaluations',120);
x = surrogateopt(objconstr,lb,ub,options)

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

x = 1×2

   -0.0904    0.7127

Linear Constraints in surrogateopt

Minimize a nonlinear objective function subject to linear inequality constraints. Minimize for 200 function evaluations.

objconstr = @multirosenbrock;
nvar = 6;
lb = -2*ones(nvar,1);
ub = -lb;
intcon = [];
A = ones(1,nvar);
b = 3;
Aeq = [];
beq = [];
options = optimoptions('surrogateopt','MaxFunctionEvaluations',200);
[sol,fval,exitflag,output] = ...
    surrogateopt(objconstr,lb,ub,intcon,A,b,Aeq,beq,options)

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

sol = 1×6

    0.1404    0.0203    0.3112    0.1215    0.1271    0.0329

fval = 2.0644

exitflag = 0

output = struct with fields:
        elapsedtime: 19.0752
          funccount: 200
    constrviolation: 0
               ineq: [1x0 double]
           rngstate: [1x1 struct]
            message: 'surrogateopt stopped because it exceeded the function evaluation limit set by ...'

Surrogate Optimization of Problem Structure

Create a problem structure representing the six-hump camel back function in the region -2.1 <= x(i) <= 2.1. Set 120 as the maximum number of function evaluations.

rng default % For reproducibility
objconstr = @(x)(4*x(:,1).^2 - 2.1*x(:,1).^4 + x(:,1).^6/3 ...
    + x(:,1).*x(:,2) - 4*x(:,2).^2 + 4*x(:,2).^4);
options = optimoptions('surrogateopt','MaxFunctionEvaluations',120);
problem = struct('objective',objconstr,...
    'lb',[-2.1,-2.1],...
    'ub',[2.1,2.1],...
    'options',options,...
    'solver','surrogateopt');
x = surrogateopt(problem)

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

x = 1×2

    0.0895   -0.7130

Return Surrogate Optimization Objective Function Value

Minimize the six-hump camel back function and return both the minimizing point and the objective function value. Set options to suppress all other display.

rng default % For reproducibility
objconstr = @(x)(4*x(:,1).^2 - 2.1*x(:,1).^4 + x(:,1).^6/3 ...
    + x(:,1).*x(:,2) - 4*x(:,2).^2 + 4*x(:,2).^4);
lb = [-2.1,-2.1];
ub = -lb;
options = optimoptions('surrogateopt','Display','off','PlotFcn',[]);
[x,fval] = surrogateopt(objconstr,lb,ub,options)

x = 1×2

    0.0895   -0.7130

fval = -1.0316

Monitor Surrogate Optimization Process

Monitor the surrogate optimization process by requesting that surrogateopt return more outputs. Use the 'surrogateoptplot' plot function. To understand the 'surrogateoptplot' plot, see Interpret surrogateoptplot.

rng default % For reproducibility
objconstr = @(x)(4*x(:,1).^2 - 2.1*x(:,1).^4 + x(:,1).^6/3 ...
    + x(:,1).*x(:,2) - 4*x(:,2).^2 + 4*x(:,2).^4);
lb = [-2.1,-2.1];
ub = -lb;
options = optimoptions('surrogateopt','PlotFcn','surrogateoptplot');
[x,fval,exitflag,output] = surrogateopt(objconstr,lb,ub,options)

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

x = 1×2

    0.0895   -0.7130

fval = -1.0316

exitflag = 0

output = struct with fields:
        elapsedtime: 45.0007
          funccount: 200
    constrviolation: 0
               ineq: [1x0 double]
           rngstate: [1x1 struct]
            message: 'surrogateopt stopped because it exceeded the function evaluation limit set by ...'

Restart Surrogate Optimization

Conclude a surrogate optimization quickly by setting a small maximum number of function evaluations. To prepare for the possibility of restarting the optimization, request all solver outputs.

rng default % For reproducibility
objconstr = @(x)(4*x(:,1).^2 - 2.1*x(:,1).^4 + x(:,1).^6/3 ...
    + x(:,1).*x(:,2) - 4*x(:,2).^2 + 4*x(:,2).^4);
lb = [-2.1,-2.1];
ub = -lb;
options = optimoptions('surrogateopt','MaxFunctionEvaluations',20);
[x,fval,exitflag,output,trials] = surrogateopt(objconstr,lb,ub,options);

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

Optimize for another 20 function evaluations, starting from the previously evaluated points.

options.InitialPoints = trials;
[x,fval,exitflag,output,trials] = surrogateopt(objconstr,lb,ub,options);

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

By comparing the plots of these 40 function evaluations to those in Search for Global Minimum, you see that restarting surrogate optimization is not the same as having the solver run continuously.

Restart Surrogate Optimization from Checkpoint File

To enable restarting surrogate optimization due to a crash or any other reason, set a checkpoint file name.

opts = optimoptions('surrogateopt','CheckpointFile','checkfile.mat');

Create an optimization problem and set a small number of function evaluations.

rng default % For reproducibility
objconstr = @(x)(4*x(:,1).^2 - 2.1*x(:,1).^4 + x(:,1).^6/3 ...
    + x(:,1).*x(:,2) - 4*x(:,2).^2 + 4*x(:,2).^4);
lb = [-2.1,-2.1];
ub = -lb;
opts.MaxFunctionEvaluations = 30;
[x,fval,exitflag,output] = surrogateopt(objconstr,lb,ub,opts)

Surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

x = 1×2

    0.0067   -0.7343

fval = -0.9986

exitflag = 0

output = struct with fields:
        elapsedtime: 28.7221
          funccount: 30
    constrviolation: 0
               ineq: [1×0 double]
           rngstate: [1×1 struct]
            message: 'Surrogateopt stopped because it exceeded the function evaluation limit set by ↵'options.MaxFunctionEvaluations'.'

Set options to use 100 function evaluations (which means 70 more than already done) and restart the optimization.

opts.MaxFunctionEvaluations = 100;
[x2,fval2,exitflag2,output2] = surrogateopt('checkfile.mat',opts)

Surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

x2 = 1×2

    0.0895   -0.7130

fval2 = -1.0316

exitflag2 = 0

output2 = struct with fields:
        elapsedtime: 159.2411
          funccount: 100
    constrviolation: 0
               ineq: [1×0 double]
           rngstate: [1×1 struct]
            message: 'Surrogateopt stopped because it exceeded the function evaluation limit set by ↵'options.MaxFunctionEvaluations'.'

Input Arguments

objconstr — Objective function and nonlinear constraint

function handle | function name

Objective function and nonlinear constraint, specified as a function handle or function name. objconstr accepts a single argument x, where x is typically a row vector. However, when the Vectorized option is true, x is a matrix containing options.BatchUpdateInterval rows; each row represents one point to evaluate. objconstr returns one of the following:

• Real scalar fval = objconstr(x).

• Structure. If the structure contains the field Fval, then surrogateopt attempts to minimize objconstr(x).Fval. If the structure contains the field Ineq, then surrogateopt attempts to make all components of that field nonpositive: objconstr(x).Ineq <= 0 for all entries. objconstr(x) must include either the Fval or Ineq fields, or both. surrogateopt ignores other fields.

When the Vectorized option is true and the BatchUpdateInterval is greater than one, objconstr operates on each row of x and returns one of the following:

• Real vector fval = objconstr(x). fval is a column vector with options.BatchUpdateInterval entries (or fewer for the last function evaluation when BatchUpdateInterval does not evenly divide MaxFunctionEvaluations).

• Structure with vector entries. If the structure contains the field Fval, then surrogateopt attempts to minimize objconstr(x).Fval, and objconstr(x).Fval is a vector of length BatchUpdateInterval (or less). If the structure contains the field Ineq, then surrogateopt attempts to make all components of that field nonpositive: objconstr(x).Ineq <= 0 for all entries, and objconstr(x).Ineq contains up to BatchUpdateInterval entries.

The objective function objconstr.Fval can be empty ([]), in which case surrogateopt attempts to find a point satisfying all the constraints. See Solve Feasibility Problem.

For examples using a nonlinear constraint, see Solve Problem with Nonlinear Constraints, Surrogate Optimization with Nonlinear Constraint, and Solve Feasibility Problem. For information on converting between the surrogateopt structure syntax and other solvers, see packfcn and Convert Nonlinear Constraints Between surrogateopt Form and Other Solver Forms For an example using vectorized batch evaluations, see Vectorized Surrogate Optimization for Custom Parallel Simulation.

Data Types: function_handle | char | string

lb — Lower bounds

finite real vector

Lower bounds, specified as a finite real vector. lb represents the lower bounds element-wise in lb ≤ x ≤ ub. The lengths of lb and ub must be equal to the number of variables that objconstr accepts.

Caution

Although lb is optional for most solvers, lb is a required input for surrogateopt.

Note

surrogateopt allows equal entries in lb and ub. For each i in intcon, you must have ceil(lb(i)) <= floor(ub(i)). See Construct Surrogate Details.

Example: lb = [0;-20;4] means x(1) ≥ 0, x(2) ≥ -20, x(3) ≥ 4.

Data Types: double

ub — Upper bounds

finite real vector

Upper bounds, specified as a finite real vector. ub represents the upper bounds element-wise in lb ≤ x ≤ ub. The lengths of lb and ub must be equal to the number of variables that objconstr accepts.

Caution

Although ub is optional for most solvers, ub is a required input for surrogateopt.

Note

surrogateopt allows equal entries in lb and ub. For each i in intcon, you must have ceil(lb(i)) <= floor(ub(i)). See Construct Surrogate Details.

Example: ub = [10;-20;4] means x(1) ≤ 10, x(2) ≤ -20, x(3) ≤ 4.

Data Types: double

intcon — Integer variables

vector of positive integers

Integer variables, specified as a vector of positive integers with values from 1 to the number of problem variables. Each value in intcon represents an x component that is integer-valued.

Example: To specify that the even entries in x are integer-valued, set intcon to 2:2:nvars.

Data Types: double

A — Linear inequality constraints

real matrix

Linear inequality constraints, specified as a real matrix. A is an M-by-nvars matrix, where M is the number of inequalities.

A encodes the M linear inequalities

A*x <= b,

where x is the column vector of nvars variables x(:), and b is a column vector with M elements.

For example, to specify

x₁ + 2x₂ ≤ 10
3x₁ + 4x₂ ≤ 20
5x₁ + 6x₂ ≤ 30,

give these constraints:

A = [1,2;3,4;5,6];
b = [10;20;30];

Example: To specify that the control variables sum to 1 or less, give the constraints A = ones(1,N) and b = 1.

Data Types: double

b — Linear inequality constraints

real vector

Linear inequality constraints, specified as a real vector. b is an M-element vector related to the A matrix. If you pass b as a row vector, solvers internally convert b to the column vector b(:).

b encodes the M linear inequalities

A*x <= b,

where x is the column vector of N variables x(:), and A is a matrix of size M-by-N.

For example, to specify

x₁ + 2x₂ ≤ 10
3x₁ + 4x₂ ≤ 20
5x₁ + 6x₂ ≤ 30,

give these constraints:

A = [1,2;3,4;5,6];
b = [10;20;30];

Example: To specify that the control variables sum to 1 or less, give the constraints A = ones(1,N) and b = 1.

Data Types: double

Aeq — Linear equality constraints

real matrix

Linear equality constraints, specified as a real matrix. Aeq is an Me-by-nvars matrix, where Me is the number of equalities.

Aeq encodes the Me linear equalities

Aeq*x = beq,

where x is the column vector of N variables x(:), and beq is a column vector with Me elements.

For example, to specify

x₁ + 2x₂ + 3x₃ = 10
2x₁ + 4x₂ + x₃ = 20,

give these constraints:

Aeq = [1,2,3;2,4,1];
beq = [10;20];

Example: To specify that the control variables sum to 1, give the constraints Aeq = ones(1,N) and beq = 1.

Data Types: double

beq — Linear equality constraints

real vector

Linear equality constraints, specified as a real vector. beq is an Me-element vector related to the Aeq matrix. If you pass beq as a row vector, solvers internally convert beq to the column vector beq(:).

beq encodes the Me linear equalities

Aeq*x = beq,

where x is the column vector of N variables x(:), and Aeq is a matrix of size Meq-by-N.

For example, to specify

x₁ + 2x₂ + 3x₃ = 10
2x₁ + 4x₂ + x₃ = 20,

give these constraints:

Aeq = [1,2,3;2,4,1];
beq = [10;20];

Example: To specify that the control variables sum to 1, give the constraints Aeq = ones(1,N) and beq = 1.

Data Types: double

options — Options

output of optimoptions

Options, specified as the output of optimoptions.

For more information, see Surrogate Optimization Options.

Option	Description	Values
BatchUpdateInterval	Number of function evaluations before the surrogate is updated. Number of points to pass in a vectorized evaluation. When UseVectorized is true, surrogateopt passes a matrix of size BatchUpdateInterval-by-nvar, where nvar is the number of problem variables. Each row of the matrix represents one evaluation point. Output functions and plot functions are updated after each batch is evaluated completely.	Positive integer. Default is 1.
CheckpointFile	File name for checkpointing and restarting optimization. The file has the .mat data type. See Work with Checkpoint Files. Checkpointing takes time. This overhead is especially noticeable for functions that otherwise take little time to evaluate.	File name or file path, given as a string or character array. If you specify a file name without a path, surrogateopt saves the checkpoint file in the current folder.
ConstraintTolerance	Tolerance on nonlinear constraints, measured as the maximum of all nonlinear constraint function values, where positive values indicate a violation. This tolerance is an absolute (not relative) tolerance; see Tolerances and Stopping Criteria.	Positive scalar. Default is 1e-3.
Display	Level of display returned at the command line.	'final' (default) — Exit message at the end of the iterations. 'off' or the equivalent 'none' — No display. 'iter' — Iterative display; see Command-Line Display.
InitialPoints	Initial points for solver.	Matrix of initial points, where each row is one point. Or, a structure with field X, whose value is a matrix of initial points, and these optional fields: Fval, a vector containing the values of the objective function at the initial points Ineq, a matrix containing nonlinear inequality constraint values See Algorithm Control. Default is [].
MaxFunctionEvaluations	Maximum number of objective function evaluations, a stopping criterion.	Positive integer. Default is max(200,50*nvar), where nvar is the number of problem variables.
MaxTime	Maximum running time in seconds. The actual running time can exceed MaxTime because of the time required to evaluate an objective function or because of parallel processing delays.	Positive scalar. Default is Inf.
MinSampleDistance	Minimum distance between trial points generated by the adaptive sampler. See Surrogate Optimization Algorithm.	Positive scalar. Default is 1e-3.
MinSurrogatePoints	Minimum number of random sample points to create at the start of a surrogate creation phase. See Surrogate Optimization Algorithm. When BatchUpdateInterval > 1, the minimum number of random sample points used to create a surrogate is the larger of MinSurrogatePoints and BatchUpdateInterval.	Integer at least nvar + 1. Default is max(20,2*nvar), where nvar is the number of problem variables.
ObjectiveLimit	Tolerance on the objective function value. If a calculated objective function value of a feasible point is less than ObjectiveLimit, the algorithm stops.	Double scalar value. Default is -Inf.
OutputFcn	Output function to report on solver progress or to stop the solver. See Output Function.	Function name, function handle, or cell array of function names or handles. Default is [].
PlotFcn	Plot function to display solver progress or to stop solver. See Plot Function.	Function name, function handle, or cell array of function names or handles. Built-in plot functions are: 'optimplotfvalconstr' (default) — Plot the best feasible objective function value found as a line plot. If there is no objective function, plot the maximum nonlinear constraint violation as a line plot. The plot shows infeasible points as red and feasible points as blue. If there is no objective function, the plot title shows the number of feasible solutions. 'optimplotfval' — Plot the best objective function value found as a line plot. 'optimplotx' — Plot the best solution found as a bar chart. 'surrogateoptplot' — Plot the objective function value at each iteration, showing which phase of the algorithm produces the value and the best value found both in this phase and overall. See Interpret surrogateoptplot.
UseParallel	Boolean value indicating whether to compute objective function values in parallel. You cannot specify both UseParallel = true and UseVectorized = true. If you set both to true, the solver ignores UseVectorized and attempts to compute in parallel using a parallel pool, if possible.	Boolean. Default is false. For algorithmic details, see Parallel surrogateopt Algorithm.
UseVectorized	Boolean value indicating whether to compute objective function values in batches of size BatchUpdateInterval. You cannot specify both UseParallel = true and UseVectorized = true. If you set both to true, the solver ignores UseVectorized and attempts to compute in parallel using a parallel pool, if possible.	Boolean. Default is false. For an example, see Vectorized Surrogate Optimization for Custom Parallel Simulation.

Example: options = optimoptions('surrogateopt','Display','iter','UseParallel',true)

problem — Problem structure

structure

Problem structure, specified as a structure with these fields:

• objective — Objective function, which can include nonlinear constraints, specified as a function name or function handle

• lb — Lower bounds for x

• ub — Upper bounds for x

• solver — 'surrogateopt'

• Aineq — Matrix for linear inequality constraints (optional)

• bineq — Vector for linear inequality constraints (optional)

• Aeq — Matrix for linear equality constraints (optional)

• beq — Vector for linear equality constraints (optional)

• options — Options created with optimoptions

• rngstate — Field to reset the state of the random number generator (optional)

• intcon — Field specifying integer-valued x components (optional)

Note

These problem fields are required: objective, lb, ub, solver, and options.

Data Types: struct

checkpointFile — Path to checkpoint file

string | character vector

Path to a checkpoint file, specified as a string or character vector. A checkpoint file has the .mat extension. If you specify a file name without a path, surrogateopt uses a checkpoint file in the current folder.

A checkpoint file stores the state of an optimization for resuming the optimization. surrogateopt updates the checkpoint file at each function evaluation, so you can resume the optimization even when surrogateopt halts prematurely. For an example, see Restart Surrogate Optimization from Checkpoint File.

surrogateopt creates a checkpoint file when it has a valid CheckpointFile option.

You can change some options when resuming from a checkpoint file. See opts.

The data in a checkpoint file is in .mat format. To avoid errors or other unexpected results, do not modify the data before calling surrogateopt.

Warning

Do not resume surrogateopt from a checkpoint file created with a different MATLAB^® version. surrogateopt can throw an error or give inconsistent results.

Example: 'checkfile.mat'

Example: "C:\Program Files\MATLAB\docs\checkpointNov2019.mat"

Data Types: char | string

opts — Options for resuming from checkpoint file

[] (default) | optimoptions options from a restricted set

Options for resuming optimization from the checkpoint file, specified as optimoptions options (from a restricted set) that you can change from the original options. The options you can change are:

• BatchUpdateInterval

• CheckpointFile

• Display

• MaxFunctionEvaluations

• MaxTime

• MinSurrogatePoints

• ObjectiveLimit

• OutputFcn

• PlotFcn

• UseParallel

• UseVectorized

Example: opts = optimoptions(options,'MaxFunctionEvaluations',400);

Output Arguments

x — Solution

real vector

Solution, returned as a real vector. x has the same length as lb and ub.

fval — Objective function value at solution

real number

Objective function value at the solution, returned as a real number.

• When objconstr returns a scalar, fval is the scalar objconstr(x).

• When objconstr returns a structure, fval is the value objconstr(x).Fval, the objective function value at x (if this value exists).

exitflag — Reason surrogateopt stopped

integer

Reason surrogateopt stopped, returned as one of the integer values described in this table.

Exit Flag	Description
10	Problem has a unique feasible solution due to one of the following: All upper bounds ub are equal to the lower bounds lb. The linear equality constraints Aeq*x = beq and the bounds have a unique solution point. surrogateopt returns the feasible point and function value without performing any optimization.
3	Feasible point found. Solver stopped because too few new feasible points were found to continue.
1	The objective function value is less than options.ObjectiveLimit. This exit flag takes precedence over exit flag 10 when both apply.
0	The number of function evaluations exceeds options.MaxFunctionEvaluations or the elapsed time exceeds options.MaxTime. If the problem has nonlinear inequalities, the solution is feasible.
-1	The optimization is terminated by an output function or plot function.
-2	No feasible point is found due to one of the following: A lower bound lb(i) exceeds a corresponding upper bound ub(i). Or one or more ceil(lb(i)) exceeds a corresponding floor(ub(i)) for i in intcon. In this case, surrogateopt returns x = [] and fval = []. lb = ub and the point lb is infeasible. In this case, x = lb, and fval = objconstr(x).Fval. The linear and, if present, integer constraints are infeasible together with the bounds. In this case, surrogateopt returns x = [] and fval = []. The bounds, integer, and linear constraints are feasible, but no feasible solution is found with nonlinear constraints. In this case, x is the point of least maximum infeasibility of nonlinear constraints, and fval = objconstr(x).Fval.

output — Information about optimization process

structure

Information about the optimization process, returned as a structure with these fields:

• funccount — Total number of function evaluations.

• elapsedtime — Time spent running the solver in seconds, as measured by tic/toc.

• message — Reason why the algorithm stopped.

• constrviolation — Maximum nonlinear constraint violation, if any. constrviolation = max(output.ineq).

• ineq — Nonlinear inequality constraint value at the solution x. If objconstr returns a structure, then ineq = objconstr(x).Ineq. Otherwise, ineq is empty.

• rngstate — State of the MATLAB random number generator just before the algorithm starts. Use this field to reproduce your results. See Reproduce Results, which discusses using rngstate for ga.

trials — Points evaluated

structure

Points evaluated, returned as a structure with these fields:

• X — Matrix with nvars columns, where nvars is the length of lb or ub. Each row of X represents one point evaluated by surrogateopt.

• Fval — Column vector, where each entry is the objective function value of the corresponding row of X.

• Ineq — Matrix with each row representing the constraint function values of the corresponding row of X.

The trials structure has the same form as the options.InitialPoints structure. So, you can continue an optimization by passing the trials structure as the InitialPoints option.

Algorithms

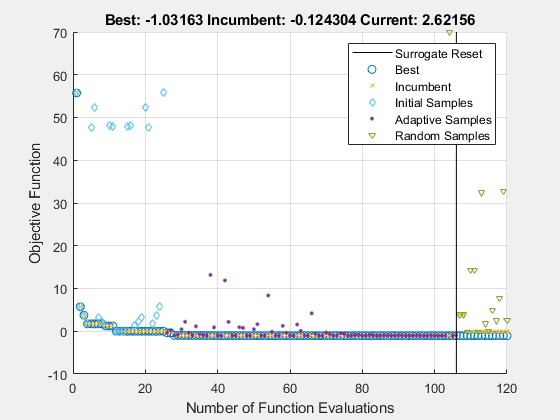
surrogateopt repeatedly performs these steps:

1. Create a set of trial points by sampling MinSurrogatePoints random points within the bounds, and evaluate the objective function at the trial points.

2. Create a surrogate model of the objective function by interpolating a radial basis function through all of the random trial points.

3. Create a merit function that gives some weight to the surrogate and some weight to the distance from the trial points. Locate a small value of the merit function by randomly sampling the merit function in a region around the incumbent point (best point found since the last surrogate reset). Use this point, called the adaptive point, as a new trial point.

4. Evaluate the objective at the adaptive point, and update the surrogate based on this point and its value. Count a "success" if the objective function value is sufficiently lower than the previous best (lowest) value observed, and count a "failure" otherwise.

5. Update the dispersion of the sample distribution upwards if three successes occur before max(nvar,5) failures, where nvar is the number of dimensions. Update the dispersion downwards if max(nvar,5) failures occur before three successes.

6. Continue from step 3 until all trial points are within MinSampleDistance of the evaluated points. At that time, reset the surrogate by discarding all adaptive points from the surrogate, reset the scale, and go back to step 1 to create MinSurrogatePoints new random trial points for evaluation.

For details, see Surrogate Optimization Algorithm.

Alternative Functionality

App

The Optimize Live Editor task provides a visual interface for surrogateopt.

Extended Capabilities

Automatic Parallel Support

Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.

To run in parallel, set the 'UseParallel' option to true.

options = optimoptions('solvername','UseParallel',true)

For more information, see How to Use Parallel Processing in Global Optimization Toolbox.