Global vs. Local Optimization Using ga
Searching for a Global Minimum
Sometimes the goal of an optimization is to find the global minimum or maximum of a function—a point where the function value is smaller or larger at any other point in the search space. However, optimization algorithms sometimes return a local minimum—a point where the function value is smaller than at nearby points, but possibly greater than at a distant point in the search space. The genetic algorithm can sometimes overcome this deficiency with the right settings.
As an example, consider the following function.
Plot the function.
t = -10:.1:103; for ii = 1:length(t) y(ii) = two_min(t(ii)); end plot(t,y)
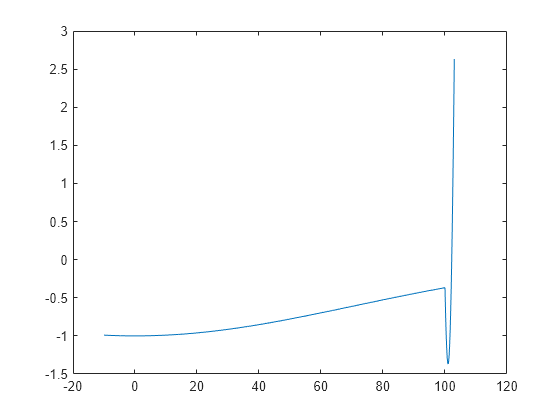
The function has two local minima, one at , where the function value is –1, and the other at , where the function value is . Since the latter value is smaller, the global minimum occurs at .
Run ga Using Default Parameters
The code for the two_min helper function is at the end of this example. Run ga with default parameters to minimize the two_min function. Use the gaplot1drange helper function (included at the end of this example) to plot the range of the ga population at each iteration.
rng default % For reproducibility options = optimoptions('ga','PlotFcn',@gaplot1drange); [x,fval] = ga(@two_min,1,[],[],[],[],[],[],[],options)
ga stopped because the average change in the fitness value is less than options.FunctionTolerance.
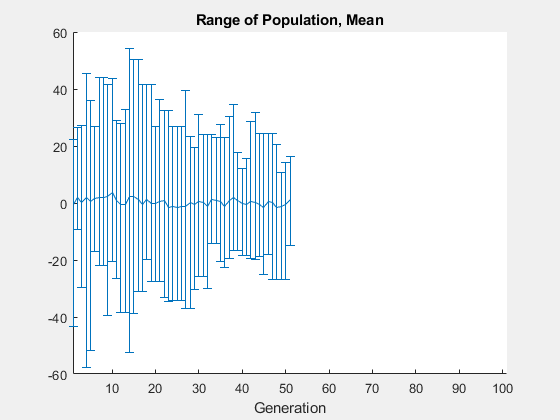
x = -0.0688
fval = -1.0000
The genetic algorithm returns a point very close to the local minimum at . Note that all individuals lie between –60 and 60. The population never explores points near the global minimum at .
Increase Initial Range
One way to make the genetic algorithm explore a wider range of points—that is, to increase the diversity of the populations—is to increase the initial range. The initial range does not have to include the point x = 101, but it must be large enough so that the algorithm generates individuals near x = 101. Set the InitialPopulationRange option to [-10;90] and rerun the solver.
options.InitialPopulationRange = [-10;90]; [x,fval] = ga(@two_min,1,[],[],[],[],[],[],[],options)
ga stopped because it exceeded options.MaxGenerations.
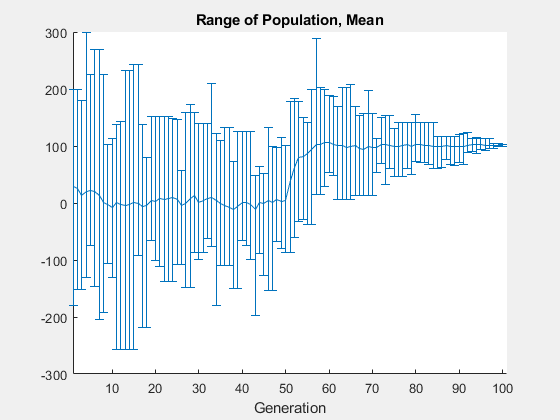
x = 100.9783
fval = -1.3674
This time, the custom plot shows a much wider range of individuals. There are individuals near 101 from early on, and the population mean begins to converge to 101.
Helper Functions
This code creates the two_min helper function.
function y = two_min(x) if x <= 100 y = -exp(-(x/100)^2); else y = -exp(-1) + (x-100)*(x-102); end end
This code creates the gaplot1drange helper function.
function state = gaplot1drange(options,state,flag) %gaplot1drange Plots the mean and the range of the population. % STATE = gaplot1drange(OPTIONS,STATE,FLAG) plots the mean and the range % (highest and the lowest) of individuals (1-D only). % % Example: % Create options that use gaplot1drange % as the plot function % options = optimoptions('ga','PlotFcn',@gaplot1drange); % Copyright 2012-2014 The MathWorks, Inc. if isinf(options.MaxGenerations) || size(state.Population,2) > 1 title('Plot Not Available','interp','none'); return; end generation = state.Generation; score = state.Population; smean = mean(score); Y = smean; L = smean - min(score); U = max(score) - smean; switch flag case 'init' set(gca,'xlim',[1,options.MaxGenerations+1]); plotRange = errorbar(generation,Y,L,U); set(plotRange,'Tag','gaplot1drange'); title('Range of Population, Mean','interp','none') xlabel('Generation','interp','none') case 'iter' plotRange = findobj(get(gca,'Children'),'Tag','gaplot1drange'); newX = [get(plotRange,'Xdata') generation]; newY = [get(plotRange,'Ydata') Y]; newL = [get(plotRange,'Ldata') L]; newU = [get(plotRange,'Udata') U]; set(plotRange,'Xdata',newX,'Ydata',newY,'Ldata',newL,'Udata',newU); end end