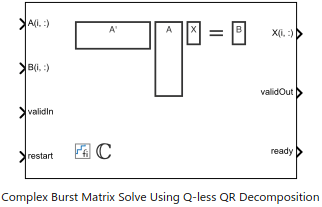
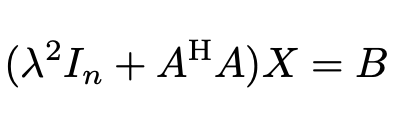Complex Burst Matrix Solve Using Q-less QR Decomposition

Compute the value of X in the equation A'AX = B for complex-valued matrices using Q-less QR decomposition

• Library:

• Fixed-Point Designer HDL Support / Matrices and Linear Algebra / Linear System Solvers

• 

×

Description

The Complex Burst Matrix Solve Using Q-less QR Decomposition block solves the system of linear equations, A'AX = B, using Q-less QR decomposition, where A and B are complex-valued matrices.

When Regularization parameter is nonzero, the Complex Burst Matrix Solve Using Q-less QR Decomposition block solves the matrix equation

$${\left[\begin{array}{c}\lambda I_n\\ A\end{array}\right]}^{\text{'}}\cdot \left[\begin{array}{c}\lambda I_n\\ A\end{array}\right]X=\left({\lambda }^2{I}_n+A\text{'}A\right)X=B$$

where λ is the regularization parameter, A is an m-by-n matrix, and I_n = eye(n).

Ports

Input

A(i,:) — Rows of matrix A

vector

Rows of matrix A, specified as a vector. A is an m-by-n matrix where m ≥ 2 and m ≥ n. If B is single or double, A must be the same data type as B. If A is a fixed-point data type, A must be signed, use binary-point scaling, and have the same word length as B. Slope-bias representation is not supported for fixed-point data types.

Data Types: single | double | fixed point
Complex Number Support: Yes

B(i,:) — Rows of matrix B

vector

Rows of matrix B, specified as a vector. B is an n-by-p matrix where n ≥ 2. If A is single or double, B must be the same data type as A. If B is a fixed-point data type, B must be signed, use binary-point scaling, and have the same word length as A. Slope-bias representation is not supported for fixed-point data types.

Data Types: single | double | fixed point

validIn — Whether inputs are valid

Boolean scalar

Whether inputs are valid, specified as a Boolean scalar. This control signal indicates when the data from the A(i,:) and B(i,:) input ports are valid. When this value is 1 (true) and the ready value is 1 (true), the block captures the values at the A(i,:) and B(i,:) input ports. When this value is 0 (false), the block ignores the input samples.

After sending a true validIn signal, there may be some delay before ready is set to false. To ensure all data is processed, you must wait until ready is set to false before sending another true validIn signal.

Data Types: Boolean

restart — Whether to clear internal states

Boolean scalar

Whether to clear internal states, specified as a Boolean scalar. When this value is 1 (true), the block stops the current calculation and clears all internal states. When this value is 0 (false) and the validIn value is 1 (true), the block begins a new subframe.

Data Types: Boolean

Output

X(i,:) — Rows of matrix X

scalar | vector

Rows of the matrix X, returned as a scalar or vector.

Data Types: single | double | fixed point

validOut — Whether output data is valid

Boolean scalar

Whether the output data is valid, returned as a Boolean scalar. This control signal indicates when the data at the output port X(i,:) is valid. When this value is 1 (true), the block has successfully computed a row of X. When this value is 0 (false), the output data is not valid.

Data Types: Boolean

ready — Whether block is ready

Boolean scalar

Whether the block is ready, returned as a Boolean scalar. This control signal indicates when the block is ready for new input data. When this value is 1 (true) and the validIn value is 1 (true), the block accepts input data in the next time step. When this value is 0 (false), the block ignores input data in the next time step.

After sending a true validIn signal, there may be some delay before ready is set to false. To ensure all data is processed, you must wait until ready is set to false before sending another true validIn signal.

Data Types: Boolean

Parameters

Number of rows in matrix A — Number of rows in matrix A

4 (default) | positive integer-valued scalar

Number of rows in matrix A, specified as a positive integer-valued scalar.

Programmatic Use

Block Parameter: m

Type: character vector

Values: positive integer-valued scalar

Default: 4

Number of columns in matrix A and rows in matrix B — Number of columns in matrix A and rows in matrix B

4 (default) | positive integer-valued scalar

Number of columns in matrix A and rows in matrix B, specified as a positive integer-valued scalar.

Programmatic Use

Block Parameter: n

Type: character vector

Values: positive integer-valued scalar

Default: 4

Number of columns in matrix B — Number of columns in matrix B

1 (default) | positive integer-valued scalar

Number of columns in matrix B, specified as a positive integer-valued scalar.

Programmatic Use

Block Parameter: p

Type: character vector

Values: positive integer-valued scalar

Default: 1

Regularization parameter — Regularization parameter

0 (default) | real nonnegative scalar

Regularization parameter, specified as a nonnegative scalar. Small, positive values of the regularization parameter can improve the conditioning of the problem and reduce the variance of the estimates. While biased, the reduced variance of the estimate often results in a smaller mean squared error when compared to least-squares estimates.

Programmatic Use

Block Parameter: regularizationParameter

Type: character vector

Values: real nonnegative scalar

Default: 0

Output datatype — Data type of output matrix X

fixdt(1,18,14) (default) | double | single | fixdt(1,16,0) | <data type expression>

Data type of the output matrix X, specified as fixdt(1,18,14), double, single, fixdt(1,16,0), or as a user-specified data type expression. The type can be specified directly, or expressed as a data type object such as Simulink.NumericType.

Programmatic Use

Block Parameter: OutputType

Type: character vector

Values: 'fixdt(1,18,14)' | 'double' | 'single' | 'fixdt(1,16,0)' | '<data type expression>'

Default: 'fixdt(1,18,14)'

Model Examples

Implement Hardware-Efficient Complex Burst Matrix Solve Using Q-less QR Decomposition

How to use the Complex Burst Matrix Solve Using Q-less QR Decomposition block.

Open Script

Implement Hardware-Efficient Complex Burst Matrix Solve Using Q-less QR Decomposition with Tikhonov Regularization

Use the Complex Burst Matrix Solve Using QR Decomposition block to solve the regularized least-squares matrix equation

Open Script

Algorithms to Determine Fixed-Point Types for Complex Q-less QR Matrix Solve A'AX=B

Derivation of algorithms for determining fixed-point types for complex Q-less QR matrix solve.

Open Live Script

Determine Fixed-Point Types for Complex Q-less QR Matrix Solve A'AX=B

Use fixed.complexQlessQRFixedpointTypes to determine fixed-point types for computation of the complex least-squares matrix equation.

Open Live Script

Determine Fixed-Point Types for Complex Q-less QR Matrix Solve with Tikhonov Regularization

Use the fixed.complexQlessQRMatrixSolveFixedpointTypes function to analytically determine fixed-point types for the solution of the complex least-squares matrix equation

Open Live Script

Tips

Use fixed.getQlessQRMatrixSolveModel(A,B) to generate a template model containing a Complex Burst Matrix Solve Using Q-less QR Decomposition block for complex-valued input matrices A and B.

Algorithms

Choosing the Implementation Method

Partial-systolic implementations prioritize speed of computations over space constraints, while burst implementations prioritize space constraints at the expense of speed of the operations. The following table illustrates the tradeoffs between the implementations available for matrix decompositions and solving systems of linear equations.

Implementation	Ready	Latency	Area
Systolic	C	O(n)	O(mn2)
Partial-Systolic	C	O(m)	O(n2)
Partial-Systolic with Forgetting Factor	C	O(n)	O(n2)
Burst	O(n)	O(mn2)	O(n)

Where C is a constant proportional to the word length of the data, m is the number of rows in matrix A, and n is the number of columns in matrix A.

For additional considerations in selecting a block for your application, see Choose a Block for HDL-Optimized Fixed-Point Matrix Operations.

Synchronous vs Asynchronous Implementation

The Matrix Solve Using QR Decomposition blocks operate synchronously. These blocks first decompose the input A and B matrices into R and C matrices using a QR decomposition block. Then, a back substitute block computes RX = C. The input A and B matrices propagate through the system in parallel, in a synchronized way.

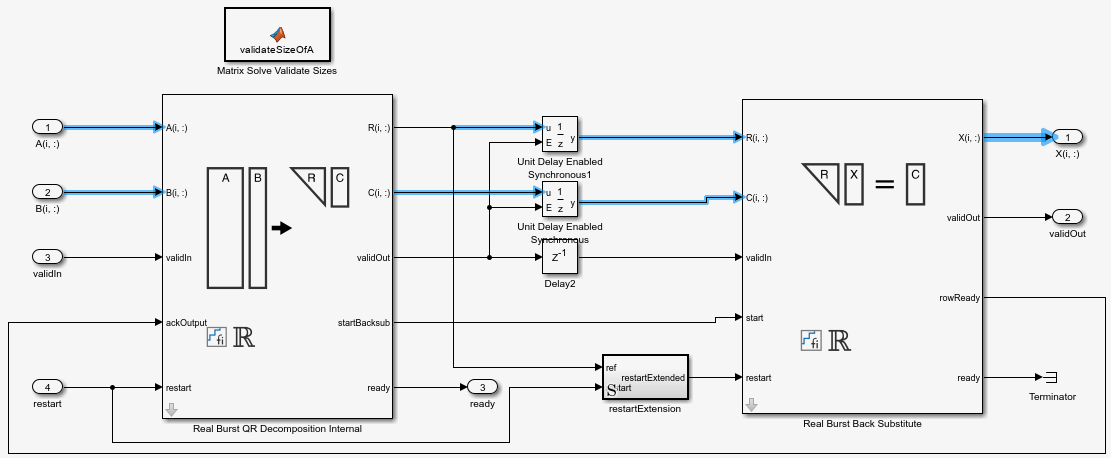
The Matrix Solve Using Q-less QR Decomposition blocks operate asynchronously. First, Q-less QR decomposition is performed on the input A matrix and the resulting R matrix is put into a buffer. Then, a forward backward substitution block uses the input B matrix and the buffered R matrix to compute R'RX = B. Because the R and B matrices are stored separately in buffers, the upstream Q-less QR decomposition block and the downstream Forward Backward Substitute block can run independently. The Forward Backward Substitute block starts processing when the first R and B matrices are available. Then it runs continuously using the latest buffered R and B matrices, regardless of the status of the Q-less QR Decomposition block. For example, if the upstream block stops providing A and B matrices, the Forward Backward Substitute block continues to generate the same output using the last pair of R and B matrices.

The Burst (Asynchronous) Matrix Solve Using Q-less QR Decomposition blocks are available in both synchronous and asynchronous operation variants, as denoted by the block name.

AMBA AXI Handshake Process

This block uses the AMBA AXI handshake protocol [1]. The valid/ready handshake process is used to transfer data and control information. This two-way control mechanism allows both the manager and subordinate to control the rate at which information moves between manager and subordinate. A valid signal indicates when data is available. The ready signal indicates that the block can accept the data. Transfer of data occurs only when both the valid and ready signals are high.

Block Timing

The Burst Matrix Solve Using QR Decomposition blocks accept and process A and B matrices row by row synchronously. After accepting m rows, the block outputs the X matrix row by row continuously. The matrix is output from the first row to the last row.

For example, assume that the input A and B matrices are 3-by-3. Additionally assume that validIn asserts before ready, meaning that the upstream data source is faster than the QR decomposition.

In the figure,

• A1r1 is the first row of the first A matrix, X1r3 is the third row of the first X matrix, and so on.

• validIn to ready — From a successful row input to the block being ready to accept the next row within one matrix.

• Last row validIn to validOut — From the last row input to the block starting to output the solution.

• Last row validIn to new matrix ready — From the block starting to output the solution to the block ready to accept the next matrix input.

The Burst Matrix Solve Using Q-less QR Decomposition blocks accept and process A and B matrices row by row synchronously. After accepting m rows, the block outputs the X matrix row by row continuously. The matrix is output from the first row to the last row.

For example, assume that the input A and B matrices are 3-by-3. Additionally assume that validIn asserts before ready, meaning that the upstream data source is faster than the QR decomposition.

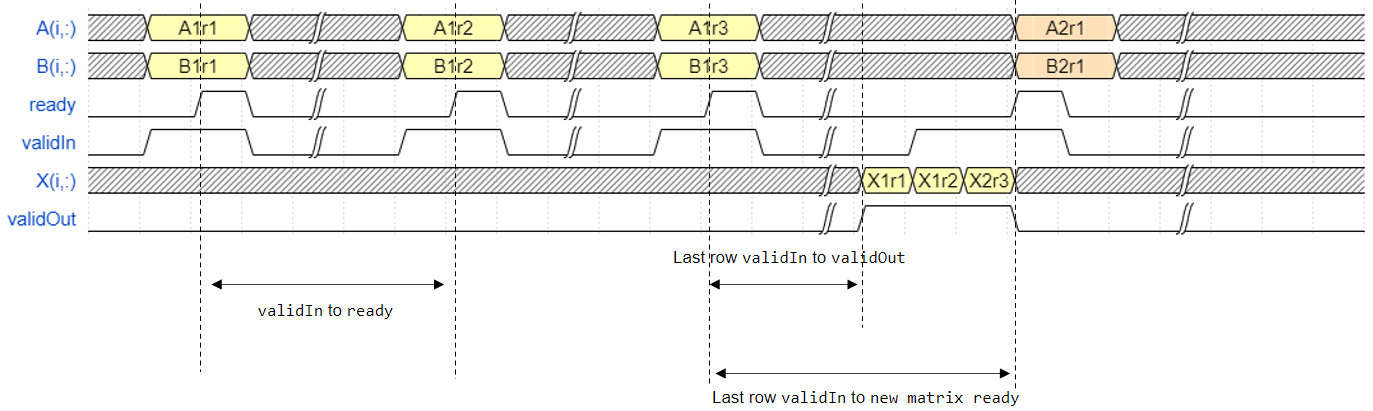
In the figure,

• A1r1 is the first row of the first A matrix, X1r3 is the third row of the first X matrix, and so on.

• validIn to ready — From a successful row input to the block being ready to accept the next row within one matrix.

• Last row validIn to validOut — From the last row input to the block starting to output the solution.

• Last row validIn to new matrix ready — From the block starting to output the solution to the block ready to accept the next matrix input.

The following table provides details of the timing for the Burst Matrix Solve Using QR Decomposition and Burst Matrix Solve Using Q-less QR Decomposition blocks.

Block	Operation	validIn to ready (cycles)	Last Row validIn to validOut (cycles)	Last row validIn to new matrix ready (cycles)
Real Burst Matrix Solve Using QR Decomposition	Synchronous	(wl + 5)*n + 2	(wl + 5)*n + 3.5*n2 + n*(nextPow2(wl) + wl + 8.5) + 3	(wl + 5)*n + 3.5*(n - 1)2 + (n - 1)(nextPow2(wl) + wl + 8.5) + 3
Complex Burst Matrix Solve Using QR Decomposition	Synchronous	(wl*2 + 11)*n + 2	(wl*2 + 11)*n + 3.5*n2 + n*(nextPow2(wl) + wl + 8.5) + 3	(wl*2 + 11)*n + 3.5*(n-1)2 + (n-1)(nextPow2(wl) + wl + 8.5) + 3
Real Burst Matrix Solve Using Q-less QR Decomposition	Synchronous	(wl + 5)*n + 2	7*n2 + 27*n + 6 + 3*n*wl + 2*n*nextPow2(wl)	7*n2 + 27*n + 6 + 3*n*wl + 2*n*nextPow2(wl) + min(m,n)
Complex Burst Matrix Solve Using Q-less QR Decomposition	Synchronous	(wl*2 + 11)*n + 2	7*22 + 33*n + 6 + 4*n*wl + 2*n*nextPow2(wl)	7*n2 + 33*n + 6 + 4*n*wl + 2*n*nextPow2(wl) + min(m,n)

In the table, m represents the number of rows in matrix A, and n is the number of columns in matrix A. wl represents the word length of A.

• If the data type of A is fixed point, then wl is the word length.

• If the data type of A is double, then wl is 53.

• If the data type of A is single, then wl is 24.

Hardware Resource Utilization

This block supports HDL code generation using the Simulink^® HDL Workflow Advisor. For an example, see HDL Code Generation and FPGA Synthesis from Simulink Model (HDL Coder) and Implement Digital Downconverter for FPGA (DSP HDL Toolbox).

This example data was generated by synthesizing the block on a Xilinx^® Zynq^® UltraScale™ + RFSoC ZCU111 evaluation board. The synthesis tool was Vivado^® v.2020.2 (win64).

The following parameters were used for synthesis.

• Block parameters:

  • m = 16

  • n = 16

  • p = 1

  • Matrix A dimension: 16-by-16

  • Matrix B dimension: 16-by-1

• Input data type: sfix16_En14

• Target frequency: 250 MHz

The following tables show the post place-and-route resource utilization results and timing summary, respectively.

Resource	Usage	Available	Utilization (%)
CLB LUTs	30915	425280	7.27
CLB Registers	34833	850560	4.10
DSPs	12	4272	0.28
Block RAM Tile	0	1080	0.00
URAM	0	80	0.00

	Value
Requirement	4 ns
Data Path Delay	3.686 ns
Slack	0.296 ns
Clock Frequency	269.98 MHz

References

[1] "AMBA AXI and ACE Protocol Specification Version E." https://developer.arm.com/documentation/ihi0022/e/AMBA-AXI3-and-AXI4-Protocol-Specification/Single-Interface-Requirements/Basic-read-and-write-transactions/Handshake-process

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using Simulink® Coder™.

Slope-bias representation is not supported for fixed-point data types.

HDL Code Generation

Generate Verilog and VHDL code for FPGA and ASIC designs using HDL Coder™.

HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.

HDL Architecture

This block has one default HDL architecture.

HDL Block Properties

General
ConstrainedOutputPipeline	Number of registers to place at the outputs by moving existing delays within your design. Distributed pipelining does not redistribute these registers. The default is 0. For more details, see ConstrainedOutputPipeline (HDL Coder).
InputPipeline	Number of input pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is 0. For more details, see InputPipeline (HDL Coder).
OutputPipeline	Number of output pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is 0. For more details, see OutputPipeline (HDL Coder).

Restrictions

Supports fixed-point data types only.

Version History

Introduced in R2020a

R2022a: Support for Tikhonov regularization parameter

The Complex Burst Matrix Solve Using Q-less QR Decomposition block now supports the Tikhonov Regularization parameter.

R2021a: Reduced HDL resource utilization

This block now has an improved algorithm to reduce resource utilization on hardware-constrained target platforms.