transprob
Estimate transition probabilities from credit ratings data
Syntax
Description
[
constructs a transition matrix from historical data of credit ratings.transMat,sampleTotals,idTotals] = transprob(data)
[
adds optional name-value pair arguments. transMat,sampleTotals,idTotals] = transprob(___,Name,Value)
Examples
Using the historical credit rating table as input data from Data_TransProb.mat display the first ten rows and compute the transition matrix:
load Data_TransProb
data(1:10,:)ans=10×3 table
ID Date Rating
____________ _______________ _______
{'00010283'} {'10-Nov-1984'} {'CCC'}
{'00010283'} {'12-May-1986'} {'B' }
{'00010283'} {'29-Jun-1988'} {'CCC'}
{'00010283'} {'12-Dec-1991'} {'D' }
{'00013326'} {'09-Feb-1985'} {'A' }
{'00013326'} {'24-Feb-1994'} {'AA' }
{'00013326'} {'10-Nov-2000'} {'BBB'}
{'00014413'} {'23-Dec-1982'} {'B' }
{'00014413'} {'20-Apr-1988'} {'BB' }
{'00014413'} {'16-Jan-1998'} {'B' }
% Estimate transition probabilities with default settings
transMat = transprob(data)transMat = 8×8
93.1170 5.8428 0.8232 0.1763 0.0376 0.0012 0.0001 0.0017
1.6166 93.1518 4.3632 0.6602 0.1626 0.0055 0.0004 0.0396
0.1237 2.9003 92.2197 4.0756 0.5365 0.0661 0.0028 0.0753
0.0236 0.2312 5.0059 90.1846 3.7979 0.4733 0.0642 0.2193
0.0216 0.1134 0.6357 5.7960 88.9866 3.4497 0.2919 0.7050
0.0010 0.0062 0.1081 0.8697 7.3366 86.7215 2.5169 2.4399
0.0002 0.0011 0.0120 0.2582 1.4294 4.2898 81.2927 12.7167
0 0 0 0 0 0 0 100.0000
Using the historical credit rating table input data from Data_TransProb.mat, compute the transition matrix using the cohort algorithm:
%Estimate transition probabilities with 'cohort' algorithm transMatCoh = transprob(data,'algorithm','cohort')
transMatCoh = 8×8
93.1345 5.9335 0.7456 0.1553 0.0311 0 0 0
1.7359 92.9198 4.5446 0.6046 0.1560 0 0 0.0390
0.1268 2.9716 91.9913 4.3124 0.4711 0.0544 0 0.0725
0.0210 0.3785 5.0683 89.7792 4.0379 0.4627 0.0421 0.2103
0.0221 0.1105 0.6851 6.2320 88.3757 3.6464 0.2873 0.6409
0 0 0.0761 0.7230 7.9909 86.1872 2.7397 2.2831
0 0 0 0.3094 1.8561 4.5630 80.8971 12.3743
0 0 0 0 0 0 0 100.0000
Using the historical credit rating data with ratings investment grade ('IG'), speculative grade ('SG'), and default ('D'), from Data_TransProb.mat display the first ten rows and compute the transition matrix:
dataIGSG(1:10,:)
ans=10×3 table
ID Date Rating
____________ _______________ ______
{'00011253'} {'04-Apr-1983'} {'IG'}
{'00012751'} {'17-Feb-1985'} {'SG'}
{'00012751'} {'19-May-1986'} {'D' }
{'00014690'} {'17-Jan-1983'} {'IG'}
{'00012144'} {'21-Nov-1984'} {'IG'}
{'00012144'} {'25-Mar-1992'} {'SG'}
{'00012144'} {'07-May-1994'} {'IG'}
{'00012144'} {'23-Jan-2000'} {'SG'}
{'00012144'} {'20-Aug-2001'} {'IG'}
{'00012937'} {'07-Feb-1984'} {'IG'}
transMatIGSG = transprob(dataIGSG,'labels',{'IG','SG','D'})
transMatIGSG = 3×3
98.6719 1.2020 0.1261
3.5781 93.3318 3.0901
0 0 100.0000
Using the historical credit rating data with numeric ratings for investment grade (1), speculative grade (2), and default (3), from Data_TransProb.mat display the first ten rows and compute the transition matrix:
dataIGSGnum(1:10,:)
ans=10×3 table
ID Date Rating
____________ _______________ ______
{'00011253'} {'04-Apr-1983'} 1
{'00012751'} {'17-Feb-1985'} 2
{'00012751'} {'19-May-1986'} 3
{'00014690'} {'17-Jan-1983'} 1
{'00012144'} {'21-Nov-1984'} 1
{'00012144'} {'25-Mar-1992'} 2
{'00012144'} {'07-May-1994'} 1
{'00012144'} {'23-Jan-2000'} 2
{'00012144'} {'20-Aug-2001'} 1
{'00012937'} {'07-Feb-1984'} 1
transMatIGSGnum = transprob(dataIGSGnum,'labels',{1,2,3})transMatIGSGnum = 3×3
98.6719 1.2020 0.1261
3.5781 93.3318 3.0901
0 0 100.0000
Using a MATLAB® table containing the historical credit rating cell array input data (dataCellFormat) from Data_TransProb.mat, estimate the transition probabilities with default settings.
load Data_TransProb
transMat = transprob(dataCellFormat)transMat = 8×8
93.1170 5.8428 0.8232 0.1763 0.0376 0.0012 0.0001 0.0017
1.6166 93.1518 4.3632 0.6602 0.1626 0.0055 0.0004 0.0396
0.1237 2.9003 92.2197 4.0756 0.5365 0.0661 0.0028 0.0753
0.0236 0.2312 5.0059 90.1846 3.7979 0.4733 0.0642 0.2193
0.0216 0.1134 0.6357 5.7960 88.9866 3.4497 0.2919 0.7050
0.0010 0.0062 0.1081 0.8697 7.3366 86.7215 2.5169 2.4399
0.0002 0.0011 0.0120 0.2582 1.4294 4.2898 81.2927 12.7167
0 0 0 0 0 0 0 100.0000
Using the historical credit rating cell array input data (dataCellFormat), compute the transition matrix using the cohort algorithm:
%Estimate transition probabilities with 'cohort' algorithm transMatCoh = transprob(dataCellFormat,'algorithm','cohort')
transMatCoh = 8×8
93.1345 5.9335 0.7456 0.1553 0.0311 0 0 0
1.7359 92.9198 4.5446 0.6046 0.1560 0 0 0.0390
0.1268 2.9716 91.9913 4.3124 0.4711 0.0544 0 0.0725
0.0210 0.3785 5.0683 89.7792 4.0379 0.4627 0.0421 0.2103
0.0221 0.1105 0.6851 6.2320 88.3757 3.6464 0.2873 0.6409
0 0 0.0761 0.7230 7.9909 86.1872 2.7397 2.2831
0 0 0 0.3094 1.8561 4.5630 80.8971 12.3743
0 0 0 0 0 0 0 100.0000
This example shows how to visualize credit rating transitions that are used as an input to the transprob function. The example also describes how the transprob function treats rating transitions when the company data starts after the start date of the analysis, or when the end date of the analysis is after the last transition observed.
Sample Data
Set up fictitious sample data for illustration purposes.
data = {'ABC','17-Feb-2015','AA';
'ABC','6-Jul-2017','A';
'LMN','12-Aug-2014','B';
'LMN','9-Nov-2015','CCC';
'LMN','7-Sep-2016','D';
'XYZ','14-May-2013','BB';
'XYZ','21-Jun-2016','BBB'};
data = cell2table(data,'VariableNames',{'ID','Date','Rating'});
disp(data) ID Date Rating
_______ _______________ _______
{'ABC'} {'17-Feb-2015'} {'AA' }
{'ABC'} {'6-Jul-2017' } {'A' }
{'LMN'} {'12-Aug-2014'} {'B' }
{'LMN'} {'9-Nov-2015' } {'CCC'}
{'LMN'} {'7-Sep-2016' } {'D' }
{'XYZ'} {'14-May-2013'} {'BB' }
{'XYZ'} {'21-Jun-2016'} {'BBB'}
The transprob function understands that this panel-data format indicates the dates when a new rating is assigned to a given company. transprob assumes that such ratings remain unchanged, unless a subsequent row explicitly indicates a rating change. For example, for company 'ABC', transprob understands that the 'A' rating is unchanged for any date after '6-Jul-2017' (indefinitely).
Compute Transition Matrix and Transition Counts
The transprob function returns a transition probability matrix as the primary output. There are also optional outputs that contain additional information for how many transitions occurred. For more information, see transprob for information on the optional outputs for both the 'cohort' and the 'duration' methods.
For illustration purposes, this example allows you to pick the StartYear (limited to 2014 or 2015 for this example) and the EndYear (2016 or 2017). This example also uses the hDisplayTransitions helper function (see the Local Functions section) to format the transitions information for ease of reading.
StartYear =2014; EndYear =
2017; startDate = datetime(StartYear,12,31,'Locale','en_US'); endDate = datetime(EndYear,12,31,'Locale','en_US'); RatingLabels = ["AAA","AA","A","BBB","BB","B","CCC","D"]; [tm,st,it] = transprob(data,'startDate',startDate,'endDate',endDate,'algorithm','cohort','labels',RatingLabels);
The transition probabilities of the TransMat output indicate the probability of migrating between ratings. The probabilities are expressed in %, that is, they are multiplied by 100.
hDisplayTransitions(tm,RatingLabels,"Transition Matrix")Transition Matrix
AAA AA A BBB BB B CCC D
___ __ ___ ___ __ _ ___ ___
AAA 100 0 0 0 0 0 0 0
AA 0 50 50 0 0 0 0 0
A 0 0 100 0 0 0 0 0
BBB 0 0 0 100 0 0 0 0
BB 0 0 0 50 50 0 0 0
B 0 0 0 0 0 0 100 0
CCC 0 0 0 0 0 0 0 100
D 0 0 0 0 0 0 0 100
The transition counts are stored in the sampleTotals optional output and indicate how many transitions occurred between ratings for the entire sample (that is, all companies).
hDisplayTransitions(st.totalsMat,RatingLabels,"Transition counts, all companies")Transition counts, all companies
AAA AA A BBB BB B CCC D
___ __ _ ___ __ _ ___ _
AAA 0 0 0 0 0 0 0 0
AA 0 1 1 0 0 0 0 0
A 0 0 0 0 0 0 0 0
BBB 0 0 0 1 0 0 0 0
BB 0 0 0 1 1 0 0 0
B 0 0 0 0 0 0 1 0
CCC 0 0 0 0 0 0 0 1
D 0 0 0 0 0 0 0 1
The third output of transprob is idTotals that contains information about transitions at an ID level, company by company (in the same order that the companies appear in the input data).
Select a company to display the transition counts and a corresponding visualization of the transitions. The hPlotTransitions helper function (see the Local Functions section) shows the transitions history for a company.
CompanyID ="ABC"; UniqueIDs = unique(data.ID,'stable'); [~,CompanyIndex] = ismember(CompanyID,UniqueIDs); hDisplayTransitions(it(CompanyIndex).totalsMat,RatingLabels,strcat("Transition counts, company ID: ",CompanyID))
Transition counts, company ID: ABC
AAA AA A BBB BB B CCC D
___ __ _ ___ __ _ ___ _
AAA 0 0 0 0 0 0 0 0
AA 0 1 1 0 0 0 0 0
A 0 0 0 0 0 0 0 0
BBB 0 0 0 0 0 0 0 0
BB 0 0 0 0 0 0 0 0
B 0 0 0 0 0 0 0 0
CCC 0 0 0 0 0 0 0 0
D 0 0 0 0 0 0 0 0
hPlotTransitions(CompanyID,startDate,endDate,data,RatingLabels)

To understand how transprob handles data when the first observed date is after the start date of the analysis, or whose last observed date occurs before the end date of the analysis, consider the following example. For company 'ABC' suppose that the analysis has a start date of 31-Dec-2014 and end date of 31-Dec-2017. There are only two transitions reported for this company for that analysis time window. The first observation for 'ABC' happened on 17-Feb-2015. So the 31-Dec-2015 snapshot is the first time the company is observed. By 31-Dec-2016, the company remained in the original 'AA' rating. By 31-Dec-2017, a downgrade to 'A' is recorded. Consistent with this, the transition counts show one transition from 'AA' to 'AA' (from the end of 2015 to the end of 2016), and one transition from 'AA' to 'A' (from the end of 2016 to the end of 2017). The plot shows the last rating as a dotted red line to emphasize that the last rating in the data is extrapolated indefinitely into the future. There is no extrapolation into the past; the company's history is ignored until a company rating is known for an entire transition period (31-Dec-2015 through 31-Dec-2016 in the case of 'ABC').
Compute Transition Matrix Containing NR (Not Rated) Rating
Consider a different sample data containing only a single company 'DEF'. The data contains transitions of company 'DEF' from 'A' to 'NR' rating and a subsequent transition from 'NR' to 'BBB'.
dataNR = {'DEF','17-Mar-2011','A';
'DEF','24-Mar-2014','NR';
'DEF','26-Sep-2016','BBB'};
dataNR = cell2table(dataNR,'VariableNames',{'ID','Date','Rating'});
disp(dataNR) ID Date Rating
_______ _______________ _______
{'DEF'} {'17-Mar-2011'} {'A' }
{'DEF'} {'24-Mar-2014'} {'NR' }
{'DEF'} {'26-Sep-2016'} {'BBB'}
transprob treats 'NR' as another rating. The transition matrix below shows the estimated probability of transitioning into and out of 'NR'.
StartYearNR = 2010; EndYearNR = 2018; startDateNR = datetime(StartYearNR,12,31,'Locale','en_US'); endDateNR = datetime(EndYearNR,12,31,'Locale','en_US'); CompanyID_NR = "DEF"; RatingLabelsNR = ["AAA","AA","A","BBB","BB","B","CCC","D","NR"]; [tmNR,~,itNR] = transprob(dataNR,'startDate',startDateNR,'endDate',endDateNR,'algorithm','cohort','labels',RatingLabelsNR); hDisplayTransitions(tmNR,RatingLabelsNR,"Transition Matrix")
Transition Matrix
AAA AA A BBB BB B CCC D NR
___ ___ ______ ___ ___ ___ ___ ___ ______
AAA 100 0 0 0 0 0 0 0 0
AA 0 100 0 0 0 0 0 0 0
A 0 0 66.667 0 0 0 0 0 33.333
BBB 0 0 0 100 0 0 0 0 0
BB 0 0 0 0 100 0 0 0 0
B 0 0 0 0 0 100 0 0 0
CCC 0 0 0 0 0 0 100 0 0
D 0 0 0 0 0 0 0 100 0
NR 0 0 0 50 0 0 0 0 50
Display the transition counts and corresponding visualization of the transitions.
hDisplayTransitions(itNR.totalsMat,RatingLabelsNR,strcat("Transition counts, company ID: ",CompanyID_NR))Transition counts, company ID: DEF
AAA AA A BBB BB B CCC D NR
___ __ _ ___ __ _ ___ _ __
AAA 0 0 0 0 0 0 0 0 0
AA 0 0 0 0 0 0 0 0 0
A 0 0 2 0 0 0 0 0 1
BBB 0 0 0 2 0 0 0 0 0
BB 0 0 0 0 0 0 0 0 0
B 0 0 0 0 0 0 0 0 0
CCC 0 0 0 0 0 0 0 0 0
D 0 0 0 0 0 0 0 0 0
NR 0 0 0 1 0 0 0 0 1
hPlotTransitions(CompanyID_NR,startDateNR,endDateNR,dataNR,RatingLabelsNR)
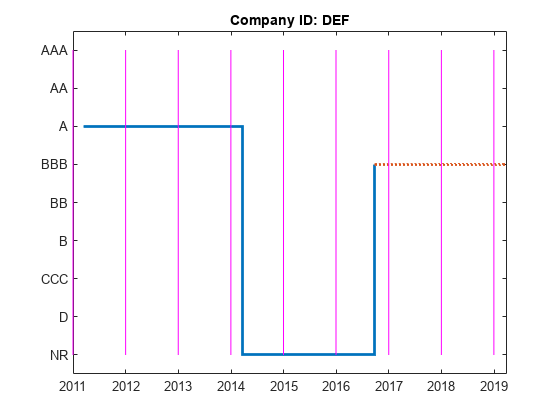
To remove the 'NR' from the transition matrix, use the 'excludeLabels' name-value input argument in transprob. The list of labels to exclude may or may not be specified in the name-value pair argument labels. For example, both RatingLabels and RatingLabelsNR generate the same output from transprob.
[tmNR,stNR,itNR] = transprob(dataNR,'startDate',startDateNR,'endDate',endDateNR,'algorithm','cohort','labels',RatingLabelsNR,'excludeLabels','NR'); hDisplayTransitions(tmNR,RatingLabels,"Transition Matrix")
Transition Matrix
AAA AA A BBB BB B CCC D
___ ___ ___ ___ ___ ___ ___ ___
AAA 100 0 0 0 0 0 0 0
AA 0 100 0 0 0 0 0 0
A 0 0 100 0 0 0 0 0
BBB 0 0 0 100 0 0 0 0
BB 0 0 0 0 100 0 0 0
B 0 0 0 0 0 100 0 0
CCC 0 0 0 0 0 0 100 0
D 0 0 0 0 0 0 0 100
Display the transition counts and corresponding visualization of the transitions.
hDisplayTransitions(itNR.totalsMat,RatingLabels,strcat("Transition counts, company ID: ",CompanyID_NR))Transition counts, company ID: DEF
AAA AA A BBB BB B CCC D
___ __ _ ___ __ _ ___ _
AAA 0 0 0 0 0 0 0 0
AA 0 0 0 0 0 0 0 0
A 0 0 2 0 0 0 0 0
BBB 0 0 0 2 0 0 0 0
BB 0 0 0 0 0 0 0 0
B 0 0 0 0 0 0 0 0
CCC 0 0 0 0 0 0 0 0
D 0 0 0 0 0 0 0 0
hPlotTransitions(CompanyID_NR,startDateNR,endDateNR,dataNR,RatingLabels)
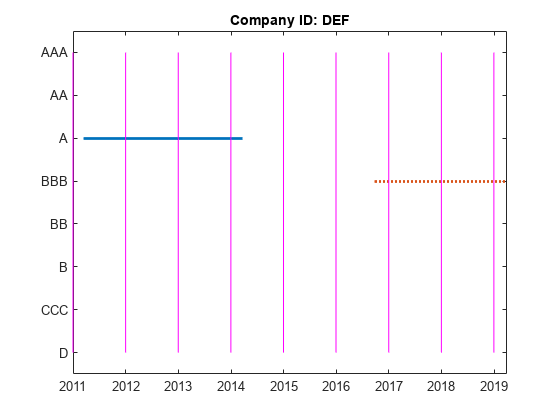
Consistent with the previous plot, the transition counts still show two transitions from 'A' to 'A' (from the end of 2012 to the end of 2014), and two transitions from 'BBB' to 'BBB' (from the end of 2017 to the end of 2019).
However, different from the previous plot, specifying 'NR' using the 'excludeLabels' name-value input argument of transprob removes any transitions into and out of the 'NR' rating.
Local Functions
function hDisplayTransitions(TransitionsData,RatingLabels,Title) % Helper function to format transition information outputs TransitionsAsTable = array2table(TransitionsData,... 'VariableNames',RatingLabels,'RowNames',RatingLabels); fprintf('\n%s\n\n',Title) disp(TransitionsAsTable) end function hPlotTransitions(CompanyID,startDate,endDate,data,RatingLabels) % Helper function to visualize transitions between ratings Ind = string(data.ID)==CompanyID; DatesOriginal = datetime(data.Date(Ind),'Locale','en_US'); RatingsOriginal = categorical(data.Rating(Ind),flipud(RatingLabels(:)),flipud(RatingLabels(:))); stairs(DatesOriginal,RatingsOriginal,'LineWidth',2) hold on; % Indicate rating extrapolated into the future (arbitrarily select 91 % days after endDate as the last date on the plot) endDateExtrap = endDate+91; if endDateExtrap>DatesOriginal(end) DatesExtrap = [DatesOriginal(end); endDateExtrap]; RatingsExtrap = [RatingsOriginal(end); RatingsOriginal(end)]; stairs(DatesExtrap,RatingsExtrap,'LineWidth',2,'LineStyle',':') end hold off; % Add lines to indicate the snapshot dates % transprob uses 1 as the default for 'snapsPerYear', hardcoded here for simplicity % The call to cfdates generates the exact same snapshot dates that transprob uses snapsPerYear = 1; snapDates = cfdates(startDate-1,endDate,snapsPerYear)'; yLimits = ylim; for ii=1:length(snapDates) line([snapDates(ii) snapDates(ii)],yLimits,'Color','m') end title(strcat("Company ID: ",CompanyID)) end
This example shows how to visualize credit rating transitions that are used as an input to the transprob function. The example also describes how the transprob function treats rating transitions when the company data starts after the start date of the analysis, or when the end date of the analysis is after the last transition observed.
Sample Data
Set up fictitious sample data for illustration purposes.
data = {'ABC','17-Feb-2015','AA';
'ABC','6-Jul-2017','A';
'LMN','12-Aug-2014','B';
'LMN','9-Nov-2015','CCC';
'LMN','7-Sep-2016','D';
'XYZ','14-May-2013','BB';
'XYZ','21-Jun-2016','BBB'};
data = cell2table(data,'VariableNames',{'ID','Date','Rating'});
disp(data) ID Date Rating
_______ _______________ _______
{'ABC'} {'17-Feb-2015'} {'AA' }
{'ABC'} {'6-Jul-2017' } {'A' }
{'LMN'} {'12-Aug-2014'} {'B' }
{'LMN'} {'9-Nov-2015' } {'CCC'}
{'LMN'} {'7-Sep-2016' } {'D' }
{'XYZ'} {'14-May-2013'} {'BB' }
{'XYZ'} {'21-Jun-2016'} {'BBB'}
The transprob function understands that this panel-data format indicates the dates when a new rating is assigned to a given company. transprob assumes that such ratings remain unchanged, unless a subsequent row explicitly indicates a rating change. For example, for company 'ABC', transprob understands that the 'A' rating is unchanged for any date after '6-Jul-2017' (indefinitely).
Compute Transition Matrix and Transition Counts
The transprob function returns a transition probability matrix as the primary output. There are also optional outputs that contain additional information for how many transitions occurred. For more information, see transprob for information on the optional outputs for both the 'cohort' and the 'duration' methods.
For illustration purposes, this example allows you to pick the StartYear (limited to 2014 or 2015 for this example) and the EndYear (2016 or 2017). This example also uses the hDisplayTransitions helper function (see the Local Functions section) to format the transitions information for ease of reading.
StartYear =2014; EndYear =
2017; startDate = datetime(StartYear,12,31,'Locale','en_US'); endDate = datetime(EndYear,12,31,'Locale','en_US'); RatingLabels = ["AAA","AA","A","BBB","BB","B","CCC","D"]; [tm,st,it] = transprob(data,'startDate',startDate,'endDate',endDate,'algorithm','cohort','labels',RatingLabels);
The transition probabilities of the TransMat output indicate the probability of migrating between ratings. The probabilities are expressed in %, that is, they are multiplied by 100.
hDisplayTransitions(tm,RatingLabels,"Transition Matrix")Transition Matrix
AAA AA A BBB BB B CCC D
___ __ ___ ___ __ _ ___ ___
AAA 100 0 0 0 0 0 0 0
AA 0 50 50 0 0 0 0 0
A 0 0 100 0 0 0 0 0
BBB 0 0 0 100 0 0 0 0
BB 0 0 0 50 50 0 0 0
B 0 0 0 0 0 0 100 0
CCC 0 0 0 0 0 0 0 100
D 0 0 0 0 0 0 0 100
The transition counts are stored in the sampleTotals optional output and indicate how many transitions occurred between ratings for the entire sample (that is, all companies).
hDisplayTransitions(st.totalsMat,RatingLabels,"Transition counts, all companies")Transition counts, all companies
AAA AA A BBB BB B CCC D
___ __ _ ___ __ _ ___ _
AAA 0 0 0 0 0 0 0 0
AA 0 1 1 0 0 0 0 0
A 0 0 0 0 0 0 0 0
BBB 0 0 0 1 0 0 0 0
BB 0 0 0 1 1 0 0 0
B 0 0 0 0 0 0 1 0
CCC 0 0 0 0 0 0 0 1
D 0 0 0 0 0 0 0 1
The third output of transprob is idTotals that contains information about transitions at an ID level, company by company (in the same order that the companies appear in the input data).
Select a company to display the transition counts and a corresponding visualization of the transitions. The hPlotTransitions helper function (see the Local Functions section) shows the transitions history for a company.
CompanyID ="ABC"; UniqueIDs = unique(data.ID,'stable'); [~,CompanyIndex] = ismember(CompanyID,UniqueIDs); hDisplayTransitions(it(CompanyIndex).totalsMat,RatingLabels,strcat("Transition counts, company ID: ",CompanyID))
Transition counts, company ID: ABC
AAA AA A BBB BB B CCC D
___ __ _ ___ __ _ ___ _
AAA 0 0 0 0 0 0 0 0
AA 0 1 1 0 0 0 0 0
A 0 0 0 0 0 0 0 0
BBB 0 0 0 0 0 0 0 0
BB 0 0 0 0 0 0 0 0
B 0 0 0 0 0 0 0 0
CCC 0 0 0 0 0 0 0 0
D 0 0 0 0 0 0 0 0
hPlotTransitions(CompanyID,startDate,endDate,data,RatingLabels)

To understand how transprob handles data when the first observed date is after the start date of the analysis, or whose last observed date occurs before the end date of the analysis, consider the following example. For company 'ABC' suppose that the analysis has a start date of 31-Dec-2014 and end date of 31-Dec-2017. There are only two transitions reported for this company for that analysis time window. The first observation for 'ABC' happened on 17-Feb-2015. So the 31-Dec-2015 snapshot is the first time the company is observed. By 31-Dec-2016, the company remained in the original 'AA' rating. By 31-Dec-2017, a downgrade to 'A' is recorded. Consistent with this, the transition counts show one transition from 'AA' to 'AA' (from the end of 2015 to the end of 2016), and one transition from 'AA' to 'A' (from the end of 2016 to the end of 2017). The plot shows the last rating as a dotted red line to emphasize that the last rating in the data is extrapolated indefinitely into the future. There is no extrapolation into the past; the company's history is ignored until a company rating is known for an entire transition period (31-Dec-2015 through 31-Dec-2016 in the case of 'ABC').
Compute Transition Matrix Containing NR (Not Rated) Rating
Consider a different sample data containing only a single company 'DEF'. The data contains transitions of company 'DEF' from 'A' to 'NR' rating and a subsequent transition from 'NR' to 'BBB'.
dataNR = {'DEF','17-Mar-2011','A';
'DEF','24-Mar-2014','NR';
'DEF','26-Sep-2016','BBB'};
dataNR = cell2table(dataNR,'VariableNames',{'ID','Date','Rating'});
disp(dataNR) ID Date Rating
_______ _______________ _______
{'DEF'} {'17-Mar-2011'} {'A' }
{'DEF'} {'24-Mar-2014'} {'NR' }
{'DEF'} {'26-Sep-2016'} {'BBB'}
transprob treats 'NR' as another rating. The transition matrix below shows the estimated probability of transitioning into and out of 'NR'.
StartYearNR = 2010; EndYearNR = 2018; startDateNR = datetime(StartYearNR,12,31,'Locale','en_US'); endDateNR = datetime(EndYearNR,12,31,'Locale','en_US'); CompanyID_NR = "DEF"; RatingLabelsNR = ["AAA","AA","A","BBB","BB","B","CCC","D","NR"]; [tmNR,~,itNR] = transprob(dataNR,'startDate',startDateNR,'endDate',endDateNR,'algorithm','cohort','labels',RatingLabelsNR); hDisplayTransitions(tmNR,RatingLabelsNR,"Transition Matrix")
Transition Matrix
AAA AA A BBB BB B CCC D NR
___ ___ ______ ___ ___ ___ ___ ___ ______
AAA 100 0 0 0 0 0 0 0 0
AA 0 100 0 0 0 0 0 0 0
A 0 0 66.667 0 0 0 0 0 33.333
BBB 0 0 0 100 0 0 0 0 0
BB 0 0 0 0 100 0 0 0 0
B 0 0 0 0 0 100 0 0 0
CCC 0 0 0 0 0 0 100 0 0
D 0 0 0 0 0 0 0 100 0
NR 0 0 0 50 0 0 0 0 50
Display the transition counts and corresponding visualization of the transitions.
hDisplayTransitions(itNR.totalsMat,RatingLabelsNR,strcat("Transition counts, company ID: ",CompanyID_NR))Transition counts, company ID: DEF
AAA AA A BBB BB B CCC D NR
___ __ _ ___ __ _ ___ _ __
AAA 0 0 0 0 0 0 0 0 0
AA 0 0 0 0 0 0 0 0 0
A 0 0 2 0 0 0 0 0 1
BBB 0 0 0 2 0 0 0 0 0
BB 0 0 0 0 0 0 0 0 0
B 0 0 0 0 0 0 0 0 0
CCC 0 0 0 0 0 0 0 0 0
D 0 0 0 0 0 0 0 0 0
NR 0 0 0 1 0 0 0 0 1
hPlotTransitions(CompanyID_NR,startDateNR,endDateNR,dataNR,RatingLabelsNR)

To remove the 'NR' from the transition matrix, use the 'excludeLabels' name-value input argument in transprob. The list of labels to exclude may or may not be specified in the name-value pair argument labels. For example, both RatingLabels and RatingLabelsNR generate the same output from transprob.
[tmNR,stNR,itNR] = transprob(dataNR,'startDate',startDateNR,'endDate',endDateNR,'algorithm','cohort','labels',RatingLabelsNR,'excludeLabels','NR'); hDisplayTransitions(tmNR,RatingLabels,"Transition Matrix")
Transition Matrix
AAA AA A BBB BB B CCC D
___ ___ ___ ___ ___ ___ ___ ___
AAA 100 0 0 0 0 0 0 0
AA 0 100 0 0 0 0 0 0
A 0 0 100 0 0 0 0 0
BBB 0 0 0 100 0 0 0 0
BB 0 0 0 0 100 0 0 0
B 0 0 0 0 0 100 0 0
CCC 0 0 0 0 0 0 100 0
D 0 0 0 0 0 0 0 100
Display the transition counts and corresponding visualization of the transitions.
hDisplayTransitions(itNR.totalsMat,RatingLabels,strcat("Transition counts, company ID: ",CompanyID_NR))Transition counts, company ID: DEF
AAA AA A BBB BB B CCC D
___ __ _ ___ __ _ ___ _
AAA 0 0 0 0 0 0 0 0
AA 0 0 0 0 0 0 0 0
A 0 0 2 0 0 0 0 0
BBB 0 0 0 2 0 0 0 0
BB 0 0 0 0 0 0 0 0
B 0 0 0 0 0 0 0 0
CCC 0 0 0 0 0 0 0 0
D 0 0 0 0 0 0 0 0
hPlotTransitions(CompanyID_NR,startDateNR,endDateNR,dataNR,RatingLabels)

Consistent with the previous plot, the transition counts still show two transitions from 'A' to 'A' (from the end of 2012 to the end of 2014), and two transitions from 'BBB' to 'BBB' (from the end of 2017 to the end of 2019).
However, different from the previous plot, specifying 'NR' using the 'excludeLabels' name-value input argument of transprob removes any transitions into and out of the 'NR' rating.
Local Functions
function hDisplayTransitions(TransitionsData,RatingLabels,Title) % Helper function to format transition information outputs TransitionsAsTable = array2table(TransitionsData,... 'VariableNames',RatingLabels,'RowNames',RatingLabels); fprintf('\n%s\n\n',Title) disp(TransitionsAsTable) end function hPlotTransitions(CompanyID,startDate,endDate,data,RatingLabels) % Helper function to visualize transitions between ratings Ind = string(data.ID)==CompanyID; DatesOriginal = datetime(data.Date(Ind),'Locale','en_US'); RatingsOriginal = categorical(data.Rating(Ind),flipud(RatingLabels(:)),flipud(RatingLabels(:))); stairs(DatesOriginal,RatingsOriginal,'LineWidth',2) hold on; % Indicate rating extrapolated into the future (arbitrarily select 91 % days after endDate as the last date on the plot) endDateExtrap = endDate+91; if endDateExtrap>DatesOriginal(end) DatesExtrap = [DatesOriginal(end); endDateExtrap]; RatingsExtrap = [RatingsOriginal(end); RatingsOriginal(end)]; stairs(DatesExtrap,RatingsExtrap,'LineWidth',2,'LineStyle',':') end hold off; % Add lines to indicate the snapshot dates % transprob uses 1 as the default for 'snapsPerYear', hardcoded here for simplicity % The call to cfdates generates the exact same snapshot dates that transprob uses snapsPerYear = 1; snapDates = cfdates(startDate-1,endDate,snapsPerYear)'; yLimits = ylim; for ii=1:length(snapDates) line([snapDates(ii) snapDates(ii)],yLimits,'Color','m') end title(strcat("Company ID: ",CompanyID)) end
This example shows how to load a historical credit rating table and then use transprob to compute the exposure-based transition matrix. The sample totals and ID totals are weighted by the exposure. For more information on the computation of transition probabilities with general weights, which specializes to exposure-based probabilities, see Algorithms.
load Data_TransProb
dataExposures(1:10,:)ans=10×4 table
ID Date Rating Exposure
_____ ___________ _______ ________
10283 10-Nov-1984 {'CCC'} 8500
10283 12-May-1986 {'B' } 8500
10283 29-Jun-1988 {'CCC'} 8500
10283 12-Dec-1991 {'D' } 8500
13326 09-Feb-1985 {'A' } 7500
13326 24-Feb-1994 {'AA' } 7500
13326 10-Nov-2000 {'BBB'} 8500
14413 23-Dec-1982 {'B' } 8500
14413 20-Apr-1988 {'BB' } 8500
14413 16-Jan-1998 {'B' } 8500
The "Weight" column is the fourth column, and in this example, it is the loan's exposure on an observation date. Note that the transprob function also supports more general weights that are only required to be nonnegative and real.
Use transprob With duration Algorithm
Use transprob to estimate the exposure based transition probabilities with default settings.
[transMatExposures,sampleTotalsExposures,idTotalsExposures] = transprob(dataExposures);
Display the exposure-based transition matrix using the default settings.
transMatExposures
transMatExposures = 8×8
92.9124 6.1143 0.7937 0.1300 0.0470 0.0013 0.0001 0.0011
1.6083 93.2741 4.2951 0.6416 0.1552 0.0056 0.0005 0.0197
0.1205 3.1292 92.0483 4.0680 0.4639 0.0845 0.0034 0.0822
0.0190 0.2259 5.0466 90.1037 3.8386 0.4605 0.0819 0.2239
0.0219 0.1085 0.5943 5.9012 89.2276 3.2159 0.2776 0.6530
0.0010 0.0057 0.0654 1.0355 7.7249 85.9825 2.6259 2.5591
0.0002 0.0012 0.0131 0.3450 1.4889 4.1707 81.6593 12.3218
0 0 0 0 0 0 0 100.0000
Display the exposure-based sample totals with default settings that use the duration algorithm.
sampleTotalsExposures.totalsVec
ans = 1×8
107 ×
1.6488 2.8735 2.8788 2.5613 2.4690 1.3158 0.6614 2.1678
sampleTotalsExposures.totalsMat
ans = 8×8
0 1081500 116000 17000 7000 0 0 0
496000 0 1326500 170000 42000 0 0 5000
29000 971000 0 1280500 118500 22000 0 22500
4000 38500 1417500 0 1090000 113000 21000 53500
5500 25500 116500 1620500 0 902500 65500 153000
0 0 3000 116000 1156500 0 411000 332500
0 0 0 21500 100500 327500 0 896000
0 0 0 0 0 0 0 0
sampleTotalsExposures.algorithm
ans = 'duration'
Display the exposure-based ID totals for the second obligor (ID 13326) with default settings that use the duration algorithm.
idTotalsExposures(2).totalsVec
ans = 1×8 sparse double row vector (3 nonzeros)
1.0e+04 *
(1,2) 5.0328
(1,3) 6.7808
(1,4) 3.6445
idTotalsExposures(2).totalsMat
ans = 8×8 sparse double matrix (2 nonzeros)
(3,2) 7500
(2,4) 7500
idTotalsExposures(2).algorithm
ans = 'duration'
Use transprob With Cohort Algorithm
Use transprob to estimate the exposure-based transition probabilities with the cohort algorithm.
[transMatCohExposures,sampleTotalsCohExposures,idTotalsCohExposures] = transprob(dataExposures,algorithm="cohort");Display the exposure-based transition matrix when using the cohort algorithm.
transMatCohExposures
transMatCohExposures = 8×8
92.9468 6.1934 0.7124 0.1044 0.0430 0 0 0
1.7148 93.0587 4.4778 0.5811 0.1497 0 0 0.0178
0.1393 3.1653 91.8358 4.2990 0.4017 0.0786 0 0.0803
0.0160 0.4148 5.1063 89.7052 4.0382 0.4529 0.0521 0.2144
0.0227 0.1054 0.5992 6.3851 88.6102 3.4198 0.2707 0.5868
0 0 0.0231 0.8706 8.3320 85.5894 2.7311 2.4538
0 0 0 0.4250 1.9731 4.3181 81.1793 12.1044
0 0 0 0 0 0 0 100.0000
Display the exposure-based sample totals when using the cohort algorithm.
sampleTotalsCohExposures.totalsVec
ans = 1×8
16283500 28049500 28006500 24949500 24197000 12980000 6588500 20952000
sampleTotalsCohExposures.totalsMat
ans = 8×8
15135000 1008500 116000 17000 7000 0 0 0
481000 26102500 1256000 163000 42000 0 0 5000
39000 886500 25720000 1204000 112500 22000 0 22500
4000 103500 1274000 22381000 1007500 113000 13000 53500
5500 25500 145000 1545000 21441000 827500 65500 142000
0 0 3000 113000 1081500 11109500 354500 318500
0 0 0 28000 130000 284500 5348500 797500
0 0 0 0 0 0 0 20952000
sampleTotalsCohExposures.algorithm
ans = 'cohort'
Display the exposure-based ID totals for the second obligor (ID 13326) when using the cohort algorithm
idTotalsCohExposures(2).totalsVec
ans = 1×8 sparse double row vector (3 nonzeros)
(1,2) 45000
(1,3) 75000
(1,4) 34000
idTotalsCohExposures(2).totalsMat
ans = 8×8 sparse double matrix (5 nonzeros)
(2,2) 37500
(3,2) 7500
(3,3) 67500
(2,4) 7500
(4,4) 34000
idTotalsCohExposures(2).algorithm
ans = 'cohort'
The duration algorithm and the cohort algorithm produce similar transition matrices. In each case, the totals are weighted by the exposures. For additional details, see Algorithms.
Input Arguments
Using transprob to estimate transition
probabilities given credit ratings historical data (that is, credit
migration data), the data input can be one of the following:
An
nRecords-by-3MATLAB® table containing the historical credit ratings data of the form:Or anID Date Rating __________ _____________ ______ '00010283' '10-Nov-1984' 'CCC' '00010283' '12-May-1986' 'B' '00010283' '29-Jun-1988' 'CCC' '00010283' '12-Dec-1991' 'D' '00013326' '09-Feb-1985' 'A' '00013326' '24-Feb-1994' 'AA' '00013326' '10-Nov-2000' 'BBB' '00014413' '23-Dec-1982' 'B'
nRecords-by-4MATLAB table containing weights and the historical credit ratings data of the form:where each row contains an ID (column 1), a date (column 2), a credit rating (column 3), and an optional weight (column 4). Column 3 is the rating assigned to the corresponding ID on the corresponding date. All information corresponding to the same ID must be stored in contiguous rows. Sorting this information by date is not required, but recommended for efficiency. When using a MATLAB table input, the names of the columns are irrelevant, but the ID, date, rating information, and weights are assumed to be in the first, second, third, and fourth columns, respectively. Also, when using a table input, the first and third columns can be categorical arrays, and the second can be a datetime array. The following summarizes the supported data types for table input:ID Date Rating Weight __________ _____________ ______ _____ '00010283' '10-Nov-1984' 'CCC' 1 '00010283' '12-May-1986' 'B' 1.4 '00010283' '29-Jun-1988' 'CCC' 1.8 '00010283' '12-Dec-1991' 'D' 0.2 '00013326' '09-Feb-1985' 'A' 0 '00013326' '24-Feb-1994' 'AA' 2 '00013326' '10-Nov-2000' 'BBB' 1.7 '00014413' '23-Dec-1982' 'B' 1.1
Data Input Type ID (1st Column) Date (2nd Column) Rating (3rd Column) Weight (Optional 4th Column) Table Numeric array
Cell array of character vectors
String array
Categorical array
Numeric array
Cell array of character vectors
String array
Datetime array
Numeric array
Cell array of character vectors
String array
Categorical array
Numeric array with nonnegative values
For an example of using the
datainput argument with an optional fourth column forWeight, see Create Exposure-Based Transition Matrix From Historical Data of Credit Ratings with Exposures.Note
If no weights are provided in a fourth column of the
data, the default is to set all weights equal to1. In this case, the weighted transition matrix output agrees with the ordinary, count-based transition matrix.An
nRecords-by-3cell array of character vectors with the historical credit ratings data of the form:Or an'00010283' '10-Nov-1984' 'CCC' '00010283' '12-May-1986' 'B' '00010283' '29-Jun-1988' 'CCC' '00010283' '12-Dec-1991' 'D' '00013326' '09-Feb-1985' 'A' '00013326' '24-Feb-1994' 'AA' '00013326' '10-Nov-2000' 'BBB' '00014413' '23-Dec-1982' 'B'
nRecords-by-4cell array of character vectors if weights are included with the historical credit ratings data of the form:where each row contains an ID (column 1), a date (column 2), a credit rating (column 3), and an optional weight (Column 4). Column 3 is the rating assigned to the corresponding ID on the corresponding date. All information corresponding to the same ID must be stored in contiguous rows. Sorting this information by date is not required, but recommended for efficiency. IDs, dates, and ratings are stored in character vector format, but they can also be entered in numeric format. The following summarizes the supported data types for cell array input:'00010283' '10-Nov-1984' 'CCC' '1.2' '00010283' '12-May-1986' 'B' '1' '00010283' '29-Jun-1988' 'CCC' '1.2' '00010283' '12-Dec-1991' 'D' '0.2' '00013326' '09-Feb-1985' 'A' '1.7' '00013326' '24-Feb-1994' 'AA' '1.3' '00013326' '10-Nov-2000' 'BBB' '1' '00014413' '23-Dec-1982' 'B' '1.8'
Data Input Type ID (1st Column) Date (2nd Column) Rating (3rd Column) Weight (Optional 4th Column) Cell Numeric elements
Character vector elements
Numeric elements
Character vector elements
Numeric elements
Character vector elements
Numeric elements with nonnegative values
Note
If no weights are provided in a fourth column of the
data, the default is to set all weights equal to1. In this case, the weighted transition matrix output agrees with the ordinary, count-based transition matrix.A preprocessed data structure obtained using
transprobprep. This data structure contains the fields'idStart','numericDates','numericRatings','Weights'(optional) , and'ratingsLabels'.
Data Types: table | cell | struct
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: transMat =
transprob(data,'algorithm','cohort')
Estimation algorithm, specified as the comma-separated pair
consisting of 'algorithm' and a character vector with
a value of 'duration' or 'cohort'.
Data Types: char
End date of the estimation time window, specified as the
comma-separated pair consisting of 'endDate' and a
scalar datetime, string, date character vector, or serial date number.
The endDate cannot be a date before the
startDate.
Data Types: char | double | string | datetime
Credit-rating scale, specified as the comma-separated pair
consisting of 'labels' and a
nRatings-by-1, or
1-by-nRatings cell array of
character vectors.
labels must be consistent with the ratings
labels used in the third column of data. Use a
cell array of numbers for numeric ratings, and a cell array for
character vectors for categorical ratings.
Note
When the input argument data is a
preprocessed data structure obtained from a previous call to
transprobprep, this optional input for
'labels is unused because the labels
in the 'ratingsLabels' field of transprobprep take priority.
Data Types: cell
Number of credit-rating snapshots per year to be considered for
the estimation, specified as the comma-separated pair consisting of
'snapsPerYear' and a numeric value of
1, 2, 3,
4, 6, or
12.
Note
This parameter is only used with the
'cohort'
algorithm.
Data Types: double
Start date of the estimation time window, specified as the
comma-separated pair consisting of 'startDate' and a
scalar datetime, string, date character vector, or serial date
number.
Data Types: char | double | string | datetime
Length of the transition interval, in years, specified as the
comma-separated pair consisting of 'transInterval'
and a numeric value.
Data Types: double
Label that is excluded from the transition probability computation,
specified as the comma-separated pair consisting of
'excludeLabels' and a character vector, string,
or numerical rating.
If multiple labels are to be excluded,
'excludeLabels' must be a cell array containing
all of the labels for exclusion. The type of the labels given in
'excludeLabels' must be consistent with the data
type specified in the labels input.
The list of labels to exclude may or may not be specified in
labels.
Data Types: double | char | string
Output Arguments
Matrix of transition probabilities in percent, returned as a
nRatings-by-nRatings
transition matrix.
Structure with sample totals, returned with fields:
totalsVec— A vector of size1-by-nRatings.totalsMat— A matrix of sizenRatings-by-nRatings.algorithm— A character vector with values'duration'or'cohort'.
For the 'duration' algorithm,
totalsMat(i,j)
contains the total weight which transitioned out of rating
i into rating j (all the diagonal
elements are zero). The total weighted time spent on rating
i is stored in
totalsVec(i). If the default
weights are used,
totalsMat(i,j)
contains the total transitions out of rating i into
rating j and
totalsVec(i) stores the total time
spent on rating i.
For example, if there are three rating categories, Investment Grade
(IG), Speculative Grade (SG), and
Default (D), and the following
information:
Total time spent IG SG D
in rating: 4859.09 1503.36 1162.05
Transitions IG SG D
out of (row) IG 0 89 7
into (column): SG 202 0 32
D 0 0 0totals.totalsVec = [4859.09 1503.36 1162.05]
totals.totalsMat = [ 0 89 7
202 0 32
0 0 0]
totals.algorithm = 'duration' For the 'cohort' algorithm,
totalsMat(i,j)
contains the total weight which is transitioned out of rating
i to rating j, and
totalsVec(i) is the initial weight
in rating i. If the default weights are used, then
totalsMat(i,j)
contains the total transitions out of rating i into
rating j and
totalsVec(i) is the initial count
in rating i.
For example, given the following information:
Initial count IG SG D
in rating: 4808 1572 1145
Transitions IG SG D
from (row) IG 4721 80 7
to (column): SG 193 1347 32
D 0 0 1145totals.totalsVec = [4808 1572 1145]
totals.totalsMat = [4721 80 7
193 1347 32
0 0 1145
totals.algorithm = 'cohort'IDs totals, returned as a struct array of size
nIDs-by-1, where
nIDs is the number of distinct IDs in column 1 of
data when this is a table or cell array or,
equivalently, equal to the length of the idStart field
minus 1 when data is a preprocessed data structure from
transprobprep. For each ID
in the sample, idTotals contains one structure with the
following fields:
totalsVec— A sparse vector of size1-by-nRatings.totalsMat— A sparse matrix of sizenRatings-by-nRatings.algorithm— A character vector with values'duration'or'cohort'.
These fields contain the same information described for the output
sampleTotals, but at an ID level. For example, for
'duration',
idTotals(k).totalsVec
contains the total time that the k-th company spent on
each rating.
More About
Transition probabilities quantify the probability of transitioning from one state (or condition) to another within a defined time frame.
The cohort algorithm estimates the transition probabilities based on a sequence of snapshots of credit ratings at regularly spaced points in time.
If the credit rating of a company changes twice between two snapshot dates, the intermediate rating is overlooked and only the initial and final ratings influence the estimates.
Unlike the cohort method, the duration algorithm estimates the transition probabilities based on the full credit ratings history, looking at the exact dates on which the credit rating migrations occur.
There is no concept of snapshots in this method, and all credit rating migrations influence the estimates, even when a company's rating changes twice within a short time.
Algorithms
The algorithm first determines a sequence
t0,...,tK
of snapshot dates. The elapsed time, in years, between two consecutive snapshot
dates tk-1 and
tk is equal to
1 / ns, where ns is the
number of snapshots per year. These K +1 dates
determine K transition periods.
The algorithm computes , the number of transition periods in which obligor n starts at rating i. These are added up over all obligors to get Ni, the number of obligors in the sample that start a period at rating i. The number periods in which obligor n starts at rating i and ends at rating j, or migrates from i to j, denoted by, is also computed. These are also added up to get , the total number of migrations from i to j in the sample.
The estimate of the transition probability from i to j in one period, denoted by, is
These probabilities are arranged in a one-period transition matrix P0, where the i,j entry in P0 is Pij.
If the number of snapshots per year ns is 4 (quarterly snapshots), the probabilities in P0 are 3-month (or 0.25-year) transition probabilities. You may, however, be interested in 1-year or 2-year transition probabilities. The latter time interval is called the transition interval, Δt, and it is used to convert P0 into the final transition matrix, P, according to the formula:
For example, if ns = 4 and
Δt = 2, P contains the
two-year transition probabilities estimated from quarterly snapshots.
When weights are provided, the calculation is similar. In this case, the number is equal to the sum of the starting weights of transition periods in which obligor n starts at rating i. These are added up over all obligors to get Ni. The quantity is computed as the sum of the starting weights of transition periods in which obligor n starts at rating i and ends at rating j. These are added up to get . The remainder of the computation proceeds as above.
Note
For the cohort algorithm, optional output arguments
idTotals and sampleTotals from
transprob contain the following information:
idTotals(n).totalsVec=idTotals(n).totalsMat=idTotals(n).algorithm='cohort'sampleTotals.totalsVec=sampleTotals.totalsMat=sampleTotals.algorithm='cohort'
For efficiency, the vectors and matrices in
idTotals are stored as sparse arrays.
When ratings must be excluded (see the excludeLabels
name-value input argument), all transitions involving the excluded ratings are
removed from the sample. For example, if the 'NR' rating must be
excluded, any transitions into 'NR' and out of
'NR' are excluded from the sample. The total counts for all
other ratings are adjusted accordingly. For more information, see Visualize Transitions Data for transprob.
The algorithm computes , the total time that obligor n spends in rating i within the estimation time window. These quantities are added up over all obligors to get , the total time spent in rating i, collectively, by all obligors in the sample. The algorithm also computes , the number times that obligor n migrates from rating i to rating j, with i not equal to j, within the estimation time window. And it also adds them up to get , the total number of migrations, by all obligors in the sample, from the rating i to j, with i not equal to j.
To estimate the transition probabilities, the duration algorithm first computes a generator matrix . Each off-diagonal entry of this matrix is an estimate of the transition rate out of rating i into rating j, and is
The diagonal entries are computed as:
With the generator matrix and the transition interval Δt (e.g.,
Δt = 2 corresponds to two-year transition
probabilities), the transition matrix is obtained as , where exp denotes matrix exponentiation
(expm in MATLAB).
When weights are provided, the calculation is similar. In this case, the number is the total weighted time that obligor n spends in rating i within the estimation window. In general, will be a sum of terms, each of which is the length of a period the obligor spent in rating i times the obligor's starting weight during that period. The quantities are added up over all obligors to get , the total weighted time spent in rating i, collectively, by all obligors in the sample. The quantity is computed as the sum of the weights of periods in which obligor n starts at rating i and ends at rating j, with i not equal to j. The remainder of the computation proceeds as above.
Note
For the duration algorithm, optional output arguments
idTotals and sampleTotals from
transprob contain the following information:
idTotals(n).totalsVec=idTotals(n).totalsMat=idTotals(n).algorithm='duration'sampleTotals.totalsVec=sampleTotals.totalsMat=sampleTotals.algorithm='duration'
For efficiency, the vectors and matrices in
idTotals are stored as sparse arrays.
When ratings must be excluded (see the excludeLabels
name-value input argument), all transitions involving the exclude ratings are
removed from the sample. For example, if the 'NR' rating must be
excluded, any transitions into 'NR' and out of
‘NR’ are excluded from the sample. The total time spent in
'NR' (or any other excluded rating) is also removed.
References
[1] Hanson, S., T. Schuermann. "Confidence Intervals for Probabilities of Default." Journal of Banking & Finance. Vol. 30(8), Elsevier, August 2006, pp. 2281–2301.
[2] Löffler, G., P. N. Posch. Credit Risk Modeling Using Excel and VBA. West Sussex, England: Wiley Finance, 2007.
[3] Schuermann, T. "Credit Migration Matrices." in E. Melnick, B. Everitt (eds.), Encyclopedia of Quantitative Risk Analysis and Assessment. Wiley, 2008.
Version History
Introduced in R2010btransprob supports an optional fourth column for weights in the
data input.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)