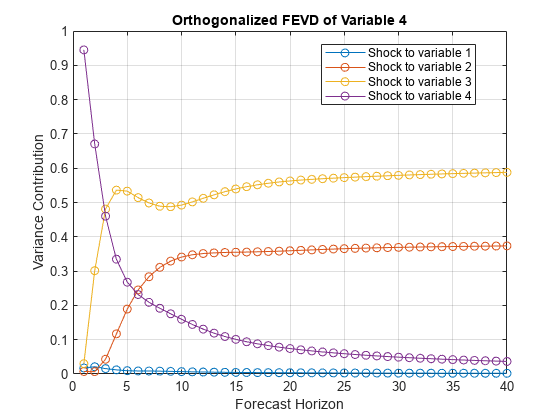
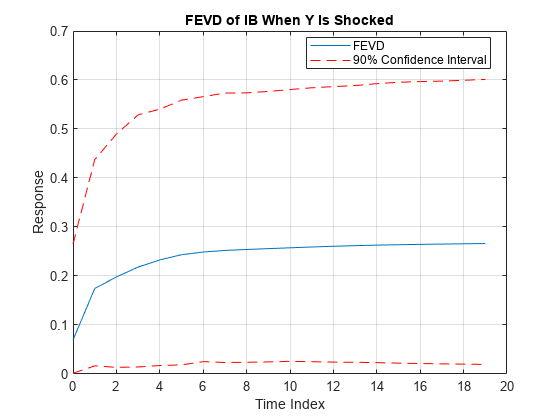
fevd

Generate vector error-correction (VEC) model forecast error variance decomposition (FEVD)

Syntax

Decomposition = fevd(Mdl)

Decomposition = fevd(Mdl,Name,Value)

[Decomposition,Lower,Upper] = fevd(___)

Description

The fevd function returns the forecast error decomposition (FEVD) of the variables in a VEC(p – 1) model attributable to shocks to each response variable in the system. A fully specified vecm model object characterizes the VEC model.

The FEVD provides information about the relative importance of each innovation in affecting the forecast error variance of all response variables in the system. In contrast, the impulse response function (IRF) traces the effects of an innovation shock to one variable on the response of all variables in the system. To estimate the IRF of a VEC model characterized by a vecm model object, see irf.

Decomposition = fevd(Mdl) returns the orthogonalized FEVDs of the response variables that compose the VEC(p – 1) model Mdl characterized by a fully specified vecm model object. fevd shocks variables at time 0, and returns the FEVD for times 1 through 20.

Decomposition = fevd(Mdl,Name,Value) uses additional options specified by one or more name-value pair arguments. For example, 'NumObs',10,'Method',"generalized" specifies estimating a generalized FEVD for times 1 through 10.

[Decomposition,Lower,Upper] = fevd(___) uses any of the input argument combinations in the previous syntaxes and returns lower and upper 95% confidence bounds for each period and variable in the FEVD.

• If you specify series of residuals by using the E name-value pair argument, then fevd estimates the confidence bounds by bootstrapping the specified residuals.

• Otherwise, fevd estimates confidence bounds by conducting Monte Carlo simulation.

If Mdl is a custom vecm model object (an object not returned by estimate or modified after estimation), fevd might require a sample size for the simulation SampleSize or presample responses Y0.

Examples

Estimate and Plot VEC Model FEVD

Fit a 4-D VEC(2) model with two cointegrating relations to Danish money and income rate series. Then, estimate and plot the orthogonalized FEVD from the estimated model.

Load the Danish money and income data set.

load Data_JDanish

The data set includes four times series in the table DataTable. For more details on the data set, enter Description at the command line.

Create a vecm model object that represents a 4-D VEC(2) model with two cointegrating relations. Specify the variable names.

Mdl = vecm(4,2,2);
Mdl.SeriesNames = DataTable.Properties.VariableNames;

Mdl is a vecm model object specifying the structure of a 4-D VEC(2) model; it is a template for estimation.

Fit the VEC(2) model to the data set.

Mdl = estimate(Mdl,DataTable.Series);

Mdl is a fully specified vecm model object representing an estimated 4-D VEC(2) model.

Estimate the orthogonalized FEVD from the estimated VEC(2) model.

Decomposition = fevd(Mdl);

Decomposition is a 20-by-4-by-4 array representing the FEVD of Mdl. Rows correspond to consecutive time points from time 1 to 20, columns correspond to variables receiving a one-standard-deviation innovation shock at time 0, and pages correspond to variables whose forecast error variance fevd decomposes. Mdl.SeriesNames specifies the variable order.

Because Decomposition represents an orthogonalized FEVD, rows should sum to 1. This characteristic illustrates that orthogonalized FEVDs represent proportions of variance contributions. Confirm that all rows of Decomposition sum to 1.

rowsums = sum(Decomposition,2);
sum((rowsums - 1).^2 > eps)

ans = 
ans(:,:,1) =

     0


ans(:,:,2) =

     0


ans(:,:,3) =

     0


ans(:,:,4) =

     0

Row sums among the pages are close to 1.

Display the contributions to the forecast error variance of the bond rate when real income is shocked at time 0.

Decomposition(:,2,3)

ans = 20×1

    0.0694
    0.1744
    0.1981
    0.2182
    0.2329
    0.2434
    0.2490
    0.2522
    0.2541
    0.2559
      ⋮

The armafevd function plots the FEVD of VAR models characterized by AR coefficient matrices. Plot the FEVD of a VEC model by:

1. Expressing the VEC(2) model as a VAR(3) model by passing Mdl to varm

2. Passing the VAR model AR coefficients and innovations covariance matrix to armafevd

Plot the VEC(2) model FEVD for 40 periods.

VARMdl = varm(Mdl);
armafevd(VARMdl.AR,[],"InnovCov",VARMdl.Covariance,...
    "NumObs",40);

Each plot shows the four FEVDs of a variable when all other variables are shocked at time 0. Mdl.SeriesNames specifies the variable order.

Estimate Generalized FEVD of VEC Model

Consider the 4-D VEC(2) model with two cointegrating relations in Estimate and Plot VEC Model FEVD. Estimate the generalized FEVD of the system for 100 periods.

Load the Danish money and income data set, then estimate the VEC(2) model.

load Data_JDanish

Mdl = vecm(4,2,2);
Mdl.SeriesNames = DataTable.Properties.VariableNames;
Mdl = estimate(Mdl,DataTable.Series);

Estimate the generalized FEVD from the estimated VEC(2) model over a forecast horizon with length 100.

Decomposition = fevd(Mdl,"Method","generalized","NumObs",100);

Decomposition is a 100-by-4-by-4 array representing the generalized FEVD of Mdl.

Plot the generalized FEVD of the bond rate when real income is shocked at time 0.

figure;
plot(1:100,Decomposition(:,2,3))
title("FEVD of IB When Y Is Shocked")
xlabel("Forecast Horizon")
ylabel("Variance Contribution")
grid on

When real income is shocked, the contribution of the bond rate to the forecast error variance settles at approximately 0.08.

Monte Carlo Confidence Intervals on True FEVD

Consider the 4-D VEC(2) model with two cointegrating relations in Estimate and Plot VEC Model FEVD. Estimate and plot its orthogonalized FEVD and 95% Monte Carlo confidence intervals on the true FEVD.

Load the Danish money and income data set, then estimate the VEC(2) model.

load Data_JDanish

Mdl = vecm(4,2,2);
Mdl.SeriesNames = DataTable.Properties.VariableNames;
Mdl = estimate(Mdl,DataTable.Series);

Estimate the FEVD and corresponding 95% Monte Carlo confidence intervals from the estimated VEC(2) model.

rng(1); % For reproducibility
[Decomposition,Lower,Upper] = fevd(Mdl);

Decomposition, Lower, and Upper are 20-by-4-by-4 arrays representing the orthogonalized FEVD of Mdl and corresponding lower and upper bounds of the confidence intervals. For all arrays, rows correspond to consecutive time points from time 1 to 20, columns correspond to variables receiving a one-standard-deviation innovation shock at time 0, and pages correspond to the variables whose forecast error variance fevd decomposes. Mdl.SeriesNames specifies the variable order.

Plot the orthogonalized FEVD with its confidence bounds of the bond rate when real income is shocked at time 0.

fevdshock2resp3 = Decomposition(:,2,3);
FEVDCIShock2Resp3 = [Lower(:,2,3) Upper(:,2,3)];

figure;
h1 = plot(1:20,fevdshock2resp3);
hold on
h2 = plot(1:20,FEVDCIShock2Resp3,'r--');
legend([h1 h2(1)],["FEVD" "95% Confidence Interval"],...
    'Location',"best")
xlabel("Forecast Horizon");
ylabel("Variance Contribution");
title("FEVD of IB When Y Is Shocked");
grid on
hold off

In the long run, and when real income is shocked, the proportion of forecast error variance of the bond rate settles between approximately 0 and 0.7 with 95% confidence.

Bootstrap Confidence Intervals on True FEVD

Consider the 4-D VEC(2) model with two cointegrating relations in Estimate and Plot VEC Model FEVD. Estimate and plot its orthogonalized FEVD and 90% bootstrap confidence intervals on the true FEVD.

Load the Danish money and income data set, then estimate the VEC(2) model. Return the residuals from model estimation.

load Data_JDanish

Mdl = vecm(4,2,2);
Mdl.SeriesNames = DataTable.Properties.VariableNames;
[Mdl,~,~,E] = estimate(Mdl,DataTable.Series);
T = size(DataTable,1) % Total sample size

T = 55

n = size(E,1)         % Effective sample size

n = 52

E is a 52-by-4 array of residuals. Columns correspond to the variables in Mdl.SeriesNames. The estimate function requires Mdl.P = 3 observations to initialize a VEC(2) model for estimation. Because presample data (Y0) is unspecified, estimate takes the first three observations in the specified response data to initialize the model. Therefore, the resulting effective sample size is T – Mdl.P = 52, and rows of E correspond to the observation indices 4 through T.

Estimate the orthogonalized FEVD and corresponding 90% bootstrap confidence intervals from the estimated VEC(2) model. Draw 500 paths of length n from the series of residuals.

rng(1); % For reproducibility
[Decomposition,Lower,Upper] = fevd(Mdl,"E",E,"NumPaths",500,...
    "Confidence",0.9);

Plot the orthogonalized FEVD with its confidence bounds of the bond rate when real income is shocked at time 0.

fevdshock2resp3 = Decomposition(:,2,3);
FEVDCIShock2Resp3 = [Lower(:,2,3) Upper(:,2,3)];

figure;
h1 = plot(0:19,fevdshock2resp3);
hold on
h2 = plot(0:19,FEVDCIShock2Resp3,'r--');
legend([h1 h2(1)],["FEVD" "90% Confidence Interval"],...
    'Location',"best")
xlabel("Time Index");
ylabel("Response");
title("FEVD of IB When Y Is Shocked");
grid on
hold off

In the long run, and when real income is shocked, the proportion of forecast error variance of the bond rate settles between approximately 0 and 0.6 with 90% confidence.

Input Arguments

Mdl — VEC model

vecm model object

VEC model, specified as a vecm model object created by vecm or estimate. Mdl must be fully specified.

Name-Value Pair Arguments

Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside quotes. You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

Example: 'NumObs',10,'Method',"generalized" specifies estimating a generalized FEVD for periods 1 through 10.

Options for All FEVDs

'NumObs' — Number of periods

20 (default) | positive integer

Number of periods for which fevd computes the FEVD (the forecast horizon), specified as the comma-separated pair consisting of 'NumObs' and a positive integer. NumObs specifies the number of observations to include in the FEVD (the number of rows in Decomposition).

Example: 'NumObs',10 specifies estimation of the FEVD for times 1 through 10.

Data Types: double

'Method' — FEVD computation method

"orthogonalized" (default) | "generalized"

FEVD computation method, specified as the comma-separated pair consisting of 'Method' and a value in this table.

Value	Description
"orthogonalized"	Compute variance decompositions using orthogonalized, one-standard-deviation innovation shocks. fevd uses the Cholesky factorization of Mdl.Covariance for orthogonalization.
"generalized"	Compute variance decompositions using one-standard-deviation innovation shocks.

Example: 'Method',"generalized"

Data Types: char | string

Options for Confidence Bound Estimation

'NumPaths' — Number of sample paths

100 (default) | positive integer

Number of sample paths (trials) to generate, specified as the comma-separated pair consisting of 'NumPaths' and a positive integer.

Example: 'NumPaths',1000 generates 1000 sample paths from which the software derives the confidence bounds.

Data Types: double

'SampleSize' — Number of observations for Monte Carlo simulation or bootstrap per sample path

positive integer

Number of observations for the Monte Carlo simulation or bootstrap per sample path, specified as the comma-separated pair consisting of 'SampleSize' and a positive integer.

• If Mdl is an estimated vecm model object (an object returned by estimate and unmodified thereafter), then the default is the sample size of the data to which the model is fit (see summarize).

• If fevd estimates confidence bounds by conducting a Monte Carlo simulation (for details, see E), you must specify SampleSize.

• If fevd estimates confidence bounds by bootstrapping residuals, the default is the length of the specified series of residuals (size(E,1)).

Example: If you specify 'SampleSize',100 and do not specify the 'E' name-value pair argument, the software estimates confidence bounds from NumPaths random paths of length 100 from Mdl.

Example: If you specify 'SampleSize',100,'E',E, the software resamples, with replacement, 100 observations (rows) from E to form a sample path of innovations to filter through Mdl. The software forms NumPaths random sample paths from which it derives confidence bounds.

Data Types: double

'Y0' — Presample response data

numeric matrix

Presample response data that provides initial values for model estimation during the simulation, specified as the comma-separated pair consisting of 'Y0' and a numpreobs-by-numseries numeric matrix.

Rows of Y0 correspond to periods in the presample, and the last row contains the latest presample response. numpreobs is the number of specified presample responses and it must be at least Mdl.P. If numpreobs exceeds Mdl.P, then fevd uses only the latest Mdl.P rows.

numseries is the dimensionality of the input VEC model Mdl.NumSeries. Columns must correspond to the response variables in Mdl.SeriesNames.

• If Mdl is an estimated vecm model object (an object returned by estimate and unmodified thereafter), fevd sets Y0 to the presample response data used for estimation by default (see 'Y0').

• Otherwise, you must specify Y0.

Data Types: double

'X' — Predictor data

numeric matrix

Predictor data for estimating the model regression component during the simulation, specified as the comma-separated pair consisting of 'X' and a numeric matrix containing numpreds columns.

numpreds is the number of predictor variables (size(Mdl.Beta,2)).

Rows correspond to observations. X must have at least SampleSize rows. If you supply more rows than necessary, fevd uses only the latest SampleSize observations. The last row contains the latest observation.

Columns correspond to individual predictor variables. All predictor variables are present in the regression component of each response equation.

To maintain model consistency when fevd estimates the confidence bounds, a good practice is to specify X when Mdl has a regression component. If Mdl is an estimated model, specify the predictor data used during model estimation (see 'X').

By default, fevd excludes the regression component from confidence bound estimation, regardless of its presence in Mdl.

Data Types: double

'E' — Series of residuals from which to draw bootstrap samples

numeric matrix

Series of residuals from which to draw bootstrap samples, specified as the comma-separated pair consisting of 'E' and a numeric matrix containing numseries columns. fevd assumes that E is free of serial correlation.

Columns contain the residual series corresponding to the response series names in Mdl.SeriesNames.

If Mdl is an estimated vecm model object (an object returned by estimate), you can specify E as the inferred residuals from estimation (see E or infer).

By default, fevd derives confidence bounds by conducting a Monte Carlo simulation.

Data Types: double

'Confidence' — Confidence level

0.95 (default) | numeric scalar in [0,1]

Confidence level for confidence bounds, specified as the comma-separated pair consisting of 'Confidence' and a numeric scalar in [0,1].

Suppose Confidence = c. Then, 100(1 – c)/2 percent of the impulse responses lie outside the confidence bounds.

The default value is 0.95, which implies that the confidence bounds represent 95% confidence intervals.

Data Types: double

'Model' — Johansen form of VEC(p – 1) model deterministic terms

"H1" (default) | "H2" | "H1*" | "H*" | "H"

Johansen form of the VEC(p – 1) model deterministic terms [2], specified as the comma-separated pair consisting of 'Model' and a value in this table (for variable definitions, see Vector Error-Correction Model).

Value	Error-Correction Term	Description
"H2"	AB´yt − 1	No intercepts or trends are present in the cointegrating relations, and no deterministic trends are present in the levels of the data. Specify this model only when all response series have a mean of zero.
"H1*"	A(B´yt−1+c0)	Intercepts are present in the cointegrating relations, and no deterministic trends are present in the levels of the data.
"H1"	A(B´yt−1+c0)+c1	Intercepts are present in the cointegrating relations, and deterministic linear trends are present in the levels of the data.
"H*"	A(B´yt−1+c0+d0t)+c1	Intercepts and linear trends are present in the cointegrating relations, and deterministic linear trends are present in the levels of the data.
"H"	A(B´yt−1+c0+d0t)+c1+d1t	Intercepts and linear trends are present in the cointegrating relations, and deterministic quadratic trends are present in the levels of the data. If quadratic trends are not present in the data, this model can produce good in-sample fits but poor out-of-sample forecasts.

For more details on the Johansen forms, see estimate.

• If Mdl is an estimated vecm model object (an object returned by estimate and unmodified thereafter), the default is the Johansen form used for estimation (see 'Model').

• Otherwise, the default is "H1".

Tip

A best practice is to maintain model consistency during the simulation that estimates confidence bounds. Therefore, if Mdl is an estimated vecm model object (an object returned by estimate and unmodified thereafter), incorporate any constraints imposed during estimation by deferring to the default value of Model.

Example: 'Model',"H1*"

Data Types: string | char

Output Arguments

Decomposition — FEVD

numeric array

FEVD of each response variable, returned as a numobs-by-numseries-by-numseries numeric array. numobs is the value of NumObs. Columns and pages correspond to the response variables in Mdl.SeriesNames.

Decomposition(t,j,k) is the contribution to the variance decomposition of variable k attributable to a one-standard-deviation innovation shock to variable j at time t, for t = 1,2,…,numobs, j = 1,2,...,numseries, and k = 1,2,...,numseries.

Lower — Lower confidence bounds

numeric array

Lower confidence bounds, returned as a numobs-by-numseries-by-numseries numeric array. Elements of Lower correspond to elements of Decomposition.

Lower(t,j,k) is the lower bound of the 100*Confidence% percentile interval on the true contribution to the variance decomposition of variable k attributable to a one-standard-deviation innovation shock to variable j at time 0.

Upper — Upper confidence bounds

numeric array

Upper confidence bounds, returned as a numobs-by-numseries-by-numseries numeric array. Elements of Upper correspond to elements of Decomposition.

Upper(t,j,k) is the upper bound of the 100*Confidence% percentile interval on the true contribution to the variance decomposition of variable k attributable to a one-standard-deviation innovation shock to variable j at time 0.

More About

Forecast Error Variance Decomposition

The forecast error variance decomposition (FEVD) of a multivariate, dynamic system shows the relative importance of a shock to each innovation in affecting the forecast error variance of all variables in the system.

Consider a numseries-D VEC(p – 1) model for the multivariate response variable y_t. In lag operator notation, the equivalent VAR(p) representation of a VEC(p – 1) model is:

$$\Gamma (L)y_t=c+dt+\beta x_t+{\epsilon }_t,$$

where $$\Gamma (L)=I-{\Gamma }_{1}L-{\Gamma }_2{L}^2-\mathrm{...}-{\Gamma }_p{L}^p$$ and I is the numseries-by-numseries identify matrix.

In lag operator notation, the infinite lag MA representation of y_t is:

$$\begin{array}{c}{y}_t={\Gamma }^{-1}(L)\left(c+\beta x_t+dt\right)+{\Gamma }^{-1}(L){\epsilon }_t\\ =\Omega (L)\left(c+\beta x_t+dt\right)+\Omega (L){\epsilon }_t.\end{array}$$

The general form of the FEVD of y_kt (variable k) m periods into the future, attributable to a one-standard-deviation innovation shock to y_jt, is

$${\gamma }_{mjk}=\frac{{\displaystyle \sum _{t=0}^{m-1}{\left(e_k{}^{\prime }{C}_t{e}_j\right)}^2}}{{\displaystyle \sum _{t=0}^{m-1}{e}_k^{\prime }{\Omega }_t\Sigma {\Omega }_t^{\prime }{e}_k}}.$$

• e_j is a selection vector of length numseries containing a 1 in element j and zeros elsewhere.

• For orthogonalized FEVDs, $$C_m={\Omega }_{m}P,$$ where P is the lower triangular factor in the Cholesky factorization of Σ.

• For generalized FEVDs, $$C_m={\sigma }_j^{-1}{\Omega }_m\Sigma ,$$ where σ_j is the standard deviation of innovation j.

• The numerator is the contribution of an innovation shock to variable j to the forecast error variance of the m-step-ahead forecast of variable k. The denominator is the mean square error (MSE) of the m-step-ahead forecast of variable k [4].

Vector Error-Correction Model

A vector error-correction (VEC) model is a multivariate, stochastic time series model consisting of a system of m = numseries equations of m distinct, differenced response variables. Equations in the system can include an error-correction term, which is a linear function of the responses in levels used to stabilize the system. The cointegrating rank r is the number of cointegrating relations that exist in the system.

Each response equation can include an autoregressive polynomial composed of first differences of the response series (short-run polynomial of degree p – 1), a constant, a time trend, exogenous predictor variables, and a constant and time trend in the error-correction term.

A VEC(p – 1) model in difference-equation notation and in reduced form can be expressed in two ways:

• This equation is the component form of a VEC model, where the cointegration adjustment speeds and cointegration matrix are explicit, whereas the impact matrix is implied.

  $$\begin{array}{c}\Delta y_t=A\left(B\prime y_{t-1}+c_0+d_{0}t\right)+c_1+d_{1}t+{\Phi }_1\Delta y_{t-1}+\mathrm{...}+{\Phi }_{p-1}\Delta y_{t-(p-1)}+\beta x_t+{\epsilon }_t\\ =c+dt+AB\prime y_{t-1}+{\Phi }_1\Delta y_{t-1}+\mathrm{...}+{\Phi }_{p-1}\Delta y_{t-(p-1)}+\beta x_t+{\epsilon }_t.\end{array}$$

  The cointegrating relations are B'y_{t – 1} + c₀ + d₀t and the error-correction term is A(B'y_{t – 1} + c₀ + d₀t).

• This equation is the impact form of a VEC model, where the impact matrix is explicit, whereas the cointegration adjustment speeds and cointegration matrix are implied.

  $$\begin{array}{c}\Delta y_t=\Pi y_{t-1}+A\left(c_0+d_{0}t\right)+c_1+d_{1}t+{\Phi }_1\Delta y_{t-1}+\mathrm{...}+{\Phi }_{p-1}\Delta y_{t-(p-1)}+\beta x_t+{\epsilon }_t\\ =c+dt+\Pi y_{t-1}+{\Phi }_1\Delta y_{t-1}+\mathrm{...}+{\Phi }_{p-1}\Delta y_{t-(p-1)}+\beta x_t+{\epsilon }_t.\end{array}$$

In the equations:

• y_t is an m-by-1 vector of values corresponding to m response variables at time t, where t = 1,...,T.

• Δy_t = y_t – y_{t – 1}. The structural coefficient is the identity matrix.

• r is the number of cointegrating relations and, in general, 0 < r < m.

• A is an m-by-r matrix of adjustment speeds.

• B is an m-by-r cointegration matrix.

• Π is an m-by-m impact matrix with a rank of r.

• c₀ is an r-by-1 vector of constants (intercepts) in the cointegrating relations.

• d₀ is an r-by-1 vector of linear time trends in the cointegrating relations.

• c₁ is an m-by-1 vector of constants (deterministic linear trends in y_t).

• d₁ is an m-by-1 vector of linear time-trend values (deterministic quadratic trends in y_t).

• c = Ac₀ + c₁ and is the overall constant.

• d = Ad₀ + d₁ and is the overall time-trend coefficient.

• Φ_j is an m-by-m matrix of short-run coefficients, where j = 1,...,p – 1 and Φ_{p – 1} is not a matrix containing only zeros.

• x_t is a k-by-1 vector of values corresponding to k exogenous predictor variables.

• β is an m-by-k matrix of regression coefficients.

• ε_t is an m-by-1 vector of random Gaussian innovations, each with a mean of 0 and collectively an m-by-m covariance matrix Σ. For t ≠ s, ε_t and ε_s are independent.

Condensed and in lag operator notation, the system is

$$\begin{array}{c}\Phi (L)(1-L)y_t=A\left(B\prime y_{t-1}+c_0+d_{0}t\right)+c_1+d_{1}t+\beta x_t+{\epsilon }_t\\ =c+dt+AB\prime y_{t-1}+\beta x_t+{\epsilon }_t\end{array}$$

where $$\Phi (L)=I-{\Phi }_1-{\Phi }_2-\mathrm{...}-{\Phi }_{p-1}$$, I is the m-by-m identity matrix, and Ly_t = y_{t – 1}.

If m = r, then the VEC model is a stable VAR(p) model in the levels of the responses. If r = 0, then the error-correction term is a matrix of zeros, and the VEC(p – 1) model is a stable VAR(p – 1) model in the first differences of the responses.

Algorithms

• If Method is "orthogonalized", then fevd orthogonalizes the innovation shocks by applying the Cholesky factorization of the model covariance matrix Mdl.Covariance. The covariance of the orthogonalized innovation shocks is the identity matrix, and the FEVD of each variable sums to one, that is, the sum along any row of Decomposition is one. Therefore, the orthogonalized FEVD represents the proportion of forecast error variance attributable to various shocks in the system. However, the orthogonalized FEVD generally depends on the order of the variables.

  If Method is "generalized", then the resulting FEVD, then the resulting FEVD is invariant to the order of the variables, and is not based on an orthogonal transformation. Also, the resulting FEVD sums to one for a particular variable only when Mdl.Covariance is diagonal[5]. Therefore, the generalized FEVD represents the contribution to the forecast error variance of equation-wise shocks to the response variables in the model.

• If Mdl.Covariance is a diagonal matrix, then the resulting generalized and orthogonalized FEVDs are identical. Otherwise, the resulting generalized and orthogonalized FEVDs are identical only when the first variable shocks all variables (in other words, all else being the same, both methods yield the same value of Decomposition(:,1,:)).

• NaN values in Y0, X, and E indicate missing data. fevd removes missing data from these arguments by list-wise deletion. Each argument, if a row contains at least one NaN, then fevd removes the entire row.

  List-wise deletion reduces the sample size, can create irregular time series, and can cause E and X to be unsynchronized.

• The predictor data X represents a single path of exogenous multivariate time series. If you specify X and the VAR model Mdl has a regression component (Mdl.Beta is not an empty array), fevd applies the same exogenous data to all paths used for confidence interval estimation.

• fevd conducts a simulation to estimate the confidence bounds Lower and Upper.

  • If you do not specify residuals E, then fevd conducts a Monte Carlo simulation by following this procedure:

    1. Simulate NumPaths response paths of length SampleSize from Mdl.

    2. Fit NumPaths models that have the same structure as Mdl to the simulated response paths. If Mdl contains a regression component and you specify X, the fevd fits the NumPaths models to the simulated response paths and X (the same predictor data for all paths).

    3. Estimate NumPaths FEVDs from the NumPaths estimated models.

    4. For each time point t = 0,…,NumObs, estimate the confidence intervals by computing 1 – Confidence and Confidence quantiles (the upper and lower bounds, respectively).

  • If you specify residuals E, then fevd conducts a nonparametric bootstrap by following this procedure:

    1. Resample, with replacement, SampleSize residuals from E. Perform this step NumPaths times to obtain NumPaths paths.

    2. Center each path of bootstrapped residuals.

    3. Filter each path of centered, bootstrapped residuals through Mdl to obtain NumPaths bootstrapped response paths of length SampleSize.

    4. Complete steps 2 through 4 of the Monte Carlo simulation, but replace the simulated response paths with the bootstrapped response paths.

References

[1] Hamilton, J. D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.

[2] Johansen, S. Likelihood-Based Inference in Cointegrated Vector Autoregressive Models. Oxford: Oxford University Press, 1995.

[3] Juselius, K. The Cointegrated VAR Model. Oxford: Oxford University Press, 2006.

[4] Lütkepohl, H. New Introduction to Multiple Time Series Analysis. New York, NY: Springer-Verlag, 2007.

[5] Pesaran, H. H., and Y. Shin. "Generalized Impulse Response Analysis in Linear Multivariate Models." Economic Letters. Vol. 58, 1998, pp. 17–29.