Model Comparison Tests

Available Tests

The primary goal of model selection is choosing the most parsimonious model that adequately fits your data. Three asymptotically equivalent tests compare a restricted model (the null model) against an unrestricted model (the alternative model), fit to the same data:

• Likelihood ratio (LR) test

• Lagrange multiplier (LM) test

• Wald (W) test

For a model with parameters θ, consider the restriction $$r(\theta )=0,$$ which is satisfied by the null model. For example, consider testing the null hypothesis $$\theta ={\theta }_0.$$ The restriction function for this test is

$$r(\theta )=\theta -{\theta }_0.$$

The LR, LM, and Wald tests approach the problem of comparing the fit of a restricted model against an unrestricted model differently. For a given data set, let $$l({\theta }_0^{MLE})$$ denote the loglikelihood function evaluated at the maximum likelihood estimate (MLE) of the restricted (null) model. Let $$l({\theta }_A^{MLE})$$ denote the loglikelihood function evaluated at the MLE of the unrestricted (alternative) model. The following figure illustrates the rationale behind each test.

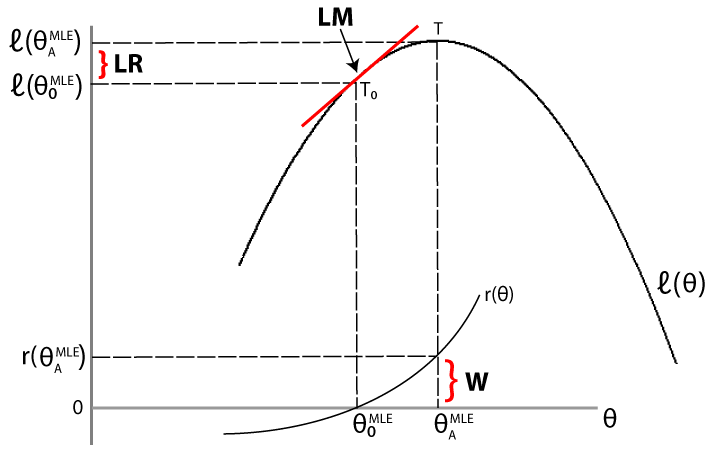
• Likelihood ratio test. If the restricted model is adequate, then the difference between the maximized objective functions, $$l({\theta }_A^{MLE})-l({\theta }_0^{MLE}),$$ should not significantly differ from zero.

• Lagrange multiplier test. If the restricted model is adequate, then the slope of the tangent of the loglikelihood function at the restricted MLE (indicated by T₀ in the figure) should not significantly differ from zero (which is the slope of the tangent of the loglikelihood function at the unrestricted MLE, indicated by T).

• Wald test. If the restricted model is adequate, then the restriction function evaluated at the unrestricted MLE should not significantly differ from zero (which is the value of the restriction function at the restricted MLE).

The three tests are asymptotically equivalent. Under the null, the LR, LM, and Wald test statistics are all distributed as $${\chi }^2$$ with degrees of freedom equal to the number of restrictions. If the test statistic exceeds the test critical value (equivalently, the p-value is less than or equal to the significance level), the null hypothesis is rejected. That is, the restricted model is rejected in favor of the unrestricted model.

Choosing among the LR, LM, and Wald test is largely determined by computational cost:

• To conduct a likelihood ratio test, you need to estimate both the restricted and unrestricted models.

• To conduct a Lagrange multiplier test, you only need to estimate the restricted model (but the test requires an estimate of the variance-covariance matrix).

• To conduct a Wald test, you only need to estimate the unrestricted model (but the test requires an estimate of the variance-covariance matrix).

All things being equal, the LR test is often the preferred choice for comparing nested models. Econometrics Toolbox™ has functionality for all three tests.

Likelihood Ratio Test

You can conduct a likelihood ratio test using lratiotest. The required inputs are:

• Value of the maximized unrestricted loglikelihood, $$l({\theta }_A^{MLE})$$

• Value of the maximized restricted loglikelihood, $$l({\theta }_0^{MLE})$$

• Number of restrictions (degrees of freedom)

Given these inputs, the likelihood ratio test statistic is

$$G^2=2\times \left[l({\theta }_A^{MLE})-l({\theta }_0^{MLE})\right].$$

When estimating conditional mean and variance models (using arima, garch, egarch, or gjr), you can return the value of the loglikelihood objective function as an optional output argument of estimate or infer. For multivariate time series models, you can get the value of the loglikelihood objective function using estimate.

Lagrange Multiplier Test

The required inputs for conducting a Lagrange multiplier test are:

• Gradient of the unrestricted likelihood evaluated at the restricted MLEs (the score), S

• Variance-covariance matrix for the unrestricted parameters evaluated at the restricted MLEs, V

Given these inputs, the LM test statistic is

$$LM=S^{\prime }VS.$$

You can conduct an LM test using lmtest. A specific example of an LM test is Engle’s ARCH test, which you can conduct using archtest.

Wald Test

The required inputs for conducting a Wald test are:

• Restriction function evaluated at the unrestricted MLE, r

• Jacobian of the restriction function evaluated at the unrestricted MLEs, R

• Variance-covariance matrix for the unrestricted parameters evaluated at the unrestricted MLEs, V

Given these inputs, the test statistic for the Wald test is

$$W=r^{\prime }{(RV{R}^{\prime })}^{-1}r.$$

You can conduct a Wald test using waldtest.

Tip

You can often compute the Jacobian of the restriction function analytically. Or, if you have Symbolic Math Toolbox™, you can use the function jacobian.

Covariance Matrix Estimation

For estimating a variance-covariance matrix, there are several common methods, including:

• Outer product of gradients (OPG). Let G be the matrix of gradients of the loglikelihood function. If your data set has N observations, and there are m parameters in the unrestricted likelihood, then G is an N × m matrix.

  The matrix $${(G^{\prime }G)}^{-1}$$ is the OPG estimate of the variance-covariance matrix.

  For arima, garch, egarch, and gjr models, the estimate method returns the OPG estimate of the variance-covariance matrix.

• Inverse negative Hessian (INH). Given the loglikelihood function $$l(\theta ),$$ the INH covariance estimate has elements

  $$\mathrm{cov}(i,j)={\left(-\frac{{\partial }^{2}l(\theta )}{\partial {\theta }_i\partial {\theta }_j}\right)}^{-1}.$$

  The estimation function for multivariate models, estimate, returns the expected Hessian variance-covariance matrix.

Tip

If you have Symbolic Math Toolbox, you can use jacobian twice to calculate the Hessian matrix for your loglikelihood function.