simulate
Simulate regression coefficients and disturbance variance of Bayesian linear regression model
Syntax
Description
[
returns a random vector of regression coefficients (BetaSim,sigma2Sim]
= simulate(Mdl)BetaSim)
and a random disturbance variance (sigma2Sim) drawn from the
Bayesian linear regression
model
Mdl of β and
σ2.
[
draws from the marginal posterior distributions produced or updated by
incorporating the predictor data BetaSim,sigma2Sim]
= simulate(Mdl,X,y)X and corresponding response
data y.
If
Mdlis a joint prior model, thensimulateproduces the marginal posterior distributions by updating the prior model with information about the parameters that it obtains from the data.If
Mdlis a marginal posterior model, thensimulateupdates the posteriors with information about the parameters that it obtains from the additional data. The complete data likelihood is composed of the additional dataXandy, and the data that createdMdl.
NaNs in the data indicate missing values, which
simulate removes by using list-wise deletion.
[
uses any of the input argument combinations in the previous syntaxes and
additional options specified by one or more name-value pair arguments. For
example, you can specify a value for β or
σ2 to simulate from the
conditional posterior distribution of one parameter,
given the specified value of the other parameter.BetaSim,sigma2Sim]
= simulate(___,Name,Value)
[
also returns draws from the latent regime distribution if BetaSim,sigma2Sim,RegimeSim]
= simulate(___)Mdl
is a Bayesian linear regression model for stochastic search variable selection
(SSVS), that is, if Mdl is a mixconjugateblm or mixsemiconjugateblm model object.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Limitations
simulatecannot draw values from an improper distribution, that is, a distribution whose density does not integrate to 1.If
Mdlis anempiricalblmmodel object, then you cannot specifyBetaorSigma2. You cannot simulate from the conditional posterior distributions by using an empirical distribution.
More About
Algorithms
Whenever
simulatemust estimate a posterior distribution (for example, whenMdlrepresents a prior distribution and you supplyXandy) and the posterior is analytically tractable,simulatesimulates directly from the posterior. Otherwise,simulateresorts to Monte Carlo simulation to estimate the posterior. For more details, see Posterior Estimation and Inference.If
Mdlis a joint posterior model, thensimulatesimulates data from it differently compared to whenMdlis a joint prior model and you supplyXandy. Therefore, if you set the same random seed and generate random values both ways, then you might not obtain the same values. However, corresponding empirical distributions based on a sufficient number of draws is effectively equivalent.This figure shows how
simulatereduces the sample by using the values ofNumDraws,Thin, andBurnIn.
Rectangles represent successive draws from the distribution.
simulateremoves the white rectangles from the sample. The remainingNumDrawsblack rectangles compose the sample.If
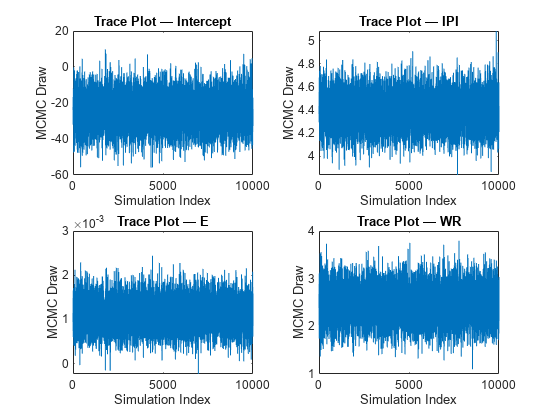
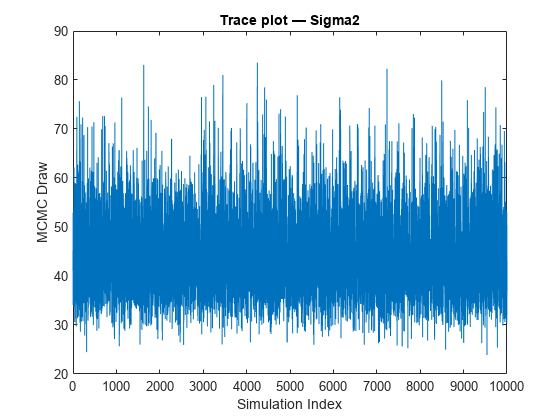
Mdlis asemiconjugateblmmodel object, thensimulatesamples from the posterior distribution by applying the Gibbs sampler.simulateuses the default value ofSigma2Startfor σ2 and draws a value of β from π(β|σ2,X,y).simulatedraws a value of σ2 from π(σ2|β,X,y) by using the previously generated value of β.The function repeats steps 1 and 2 until convergence. To assess convergence, draw a trace plot of the sample.
If you specify
BetaStart, thensimulatedraws a value of σ2 from π(σ2|β,X,y) to start the Gibbs sampler.simulatedoes not return this generated value of σ2.If
Mdlis anempiricalblmmodel object and you do not supplyXandy, thensimulatedraws fromMdl.BetaDrawsandMdl.Sigma2Draws. IfNumDrawsis less than or equal tonumel(Mdl.Sigma2Draws), thensimulatereturns the firstNumDrawselements ofMdl.BetaDrawsandMdl.Sigma2Drawsas random draws for the corresponding parameter. Otherwise,simulaterandomly resamplesNumDrawselements fromMdl.BetaDrawsandMdl.Sigma2Draws.If
Mdlis acustomblmmodel object, thensimulateuses an MCMC sampler to draw from the posterior distribution. At each iteration, the software concatenates the current values of the regression coefficients and disturbance variance into an (Mdl.Intercept+Mdl.NumPredictors+ 1)-by-1 vector, and passes it toMdl.LogPDF. The value of the disturbance variance is the last element of this vector.The HMC sampler requires both the log density and its gradient. The gradient should be a
(NumPredictors+Intercept+1)-by-1 vector. If the derivatives of certain parameters are difficult to compute, then, in the corresponding locations of the gradient, supplyNaNvalues instead.simulatereplacesNaNvalues with numerical derivatives.If
Mdlis alassoblm,mixconjugateblm, ormixsemiconjugateblmmodel object and you supplyXandy, thensimulatesamples from the posterior distribution by applying the Gibbs sampler. If you do not supply the data, thensimulatesamples from the analytical, unconditional prior distributions.simulatedoes not return default starting values that it generates.If
Mdlis amixconjugateblmormixsemiconjugateblm, thensimulatedraws from the regime distribution first, given the current state of the chain (the values ofRegimeStart,BetaStart, andSigma2Start). If you draw one sample and do not specify values forRegimeStart,BetaStart, andSigma2Start, thensimulateuses the default values and issues a warning.
Version History
Introduced in R2017a
See Also
Objects
conjugateblm|customblm|empiricalblm|semiconjugateblm|diffuseblm|mixconjugateblm|mixsemiconjugateblm|lassoblm