FIR Decimator
Finite impulse response (FIR) decimation filter
Libraries:
DSP HDL Toolbox /
Filtering
Description
The FIR Decimator block implements a single-rate polyphase FIR decimation filter that is optimized for HDL code generation. The block provides a hardware-friendly interface with input and output control signals. To provide a cycle-accurate simulation of the generated HDL code, the block models architectural latency including pipeline registers and resource sharing.
The block accepts scalar or vector input. When you use vector input and the vector size is less than the decimation factor, the decimation factor must be an integer multiple of the vector size. In this case, the output is scalar and an output valid signal indicates which samples are valid after decimation. The output data is valid every DecimationFactor/VectorSize samples. The waveform shows an input vector of four samples and a decimation factor of eight. The output data is a scalar that is valid every second cycle.

When you use vector input and the vector size is greater than the decimation factor, the vector size must be an integer multiple of the decimation factor. In this case, the output is a vector of VectorSize/DecimationFactor samples. The waveform shows an input vector of eight samples and a decimation factor of four. The output data is a vector of two samples on every cycle.

The block provides two filter structures. The direct form systolic architecture provides an implementation that makes efficient use of Intel® and Xilinx® DSP blocks. This architecture can be fully parallel or serial. To use a serial architecture, the input samples must be spaced out with a regular number of invalid cycles between the valid samples. The direct form transposed architecture is a fully parallel implementation that is suitable for FPGA and ASIC applications. For a filter implementation that matches multipliers, pipeline registers, and pre-adders to the DSP configuration of your FPGA vendor, specify your target device when you generate HDL code.
All filter structures optimize hardware resources by sharing multipliers for symmetric or antisymmetric filters and by removing the multipliers for zero-valued coefficients such as in half-band filters and Hilbert transforms.
The block implements one filter for each sample in the input vector. The block then shares this filter between the polyphase subfilters by interleaving the subfilter coefficients in time.
Note
You can also generate HDL code for this hardware-optimized algorithm, without creating a Simulink® model, by using the DSP HDL IP Designer app. The app provides the same interface and configuration options as the Simulink block.
Examples
FIR Decimation for FPGA
Decimate streaming samples using a hardware-friendly polyphase FIR filter.
Implement Digital Downconverter for FPGA
Design a digital downconverter (DDC) for LTE on FPGAs.
Ports
Input
Input data must be a real- or complex-valued scalar or vector. When you use vector input and the vector size is less than the decimation factor, the decimation factor must be an integer multiple of the vector size. When you use vector input and the vector size is greater than the decimation factor, the vector size must be an integer multiple of the decimation factor. The vector size must be less than or equal to 64.
When the input data type is an integer type or a fixed-point type, the block uses fixed-point arithmetic for internal calculations.
The software supports double and
single data types for simulation, but not for HDL code generation.
Data Types: fixed point | single | double | int8 | int16 | int32 | uint8 | uint16 | uint32
Complex Number Support: Yes
Control signal that indicates if the input data is valid.
When valid is 1
(true), the block captures the
values from the input data port. When
valid is 0
(false), the block ignores the
values from the input data
port.
Data Types: Boolean
Since R2025a
Filter coefficients, specified as a row vector of real or complex values. You can change the input coefficients at any time. The size of the coefficient vector must match the size of the sample coefficients specified in the Coefficients prototype parameter. The prototype specifies a sample coefficient vector that is representative of the zero-valued locations of the expected input coefficients. The block uses the prototype to optimize the filter by removing multipliers for zero-valued coefficients.
If the input data is a fixed-point type, the coeff values must also be of a fixed point type. If the input data is a floating-point data type, the coeff values must be of the same data type.
The software supports double and
single data types for simulation, but not for HDL code generation.
Dependencies
To enable this port, set Coefficients
source to Input port
(Parallel interface).
Data Types: fixed point | int8 | int16 | int32 | uint8 | uint16 | uint32 | single | double
Control signal that clears internal states. When
reset is 1
(true), the block stops the
current calculation and clears internal states. When the
reset is 0
(false) and the input
valid is 1
(true), the block captures data
for processing.
For more reset considerations, see the Reset Signal section on the Hardware Control Signals page.
Dependencies
To enable this port, on the Control Ports tab, select Enable reset input port.
Data Types: Boolean
Output
Filtered output data, returned as a real- or complex-valued scalar. When the input data type is a floating-point type, the output data inherits the data type of the input data. When the input data type is an integer type or a fixed-point type, the Output parameter on the Data Types tab specifies the output data type.
The output valid signal indicates which samples are valid after decimation. When the input vector size is greater than the decimation factor, the output is a vector of VectorSize/DecimationFactor samples.
Data Types: fixed point | single | double
Complex Number Support: Yes
Control signal that indicates if the data from the output
data port is valid. When
valid is 1
(true), the block returns valid
data from the output data port. When
valid is 0
(false), the values from the
output data port are not
valid.
Data Types: Boolean
Parameters
Main
Since R2025a
You can enter constant filter coefficients as a parameter or provide time-varying filter coefficients by using an input port.
When you select Input port (Parallel
interface), the
coeff port appears on the
block.
Selecting Input port (Parallel
interface)
enables the Coefficients prototype
parameter. Specify a prototype to enable the block to
optimize the filter implementation according to the values
of the coefficients.
When you use programmable coefficients with frame-based input, the output after a change of coefficient values might not match the output in the scalar case exactly. This difference occurs because the subfilter calculations are performed at different times relative to the input coefficient values, compared with the scalar implementation.
FIR filter coefficients, specified as a real- or complex-valued vector. You can specify the vector as a workspace variable or as a call to a filter design function. When the input data type is a floating-point type, the block casts the coefficients to the same data type as the input. When the input data type is an integer type or a fixed-point type, set the data type for the coefficients on the Data Types tab.
Example: firpm(30,[0 0.1 0.2 0.5]*2,[1 1 0
0]) defines coefficients using a
linear-phase filter design function.
Dependencies
To enable this parameter, set Coefficients
source to
Property.
Complex Number Support: Yes
Since R2025a
Prototype filter coefficients, specified as a vector of real or complex values. The prototype specifies a sample coefficient vector that is representative of the zero-valued locations of the expected input coefficients. If all input coefficient vectors have the same zero-valued coefficient locations, set Coefficients prototype to one of those vectors. The block uses the prototype to optimize the filter by removing multipliers for zero-valued coefficients.
Dependencies
To enable this parameter, set Coefficients
source to Input port
(Parallel
interface).
The block implements a polyphase decomposition filter by using Discrete FIR Filter blocks. Both structures share resources by interleaving the subfilter coefficients over one filter implementation for each sample in the input vector. Specify the HDL filter architecture as one of these structures:
Direct form systolic— This architecture provides a parallel or partly serial filter implementation that makes efficient use of Intel and Xilinx DSP blocks. For a partly serial implementation, specify a value greater than 1 for the Minimum number of cycles between valid input samples parameter. You cannot use frame-based input with the partly serial architecture.When Minimum number of cycles between valid input samples is greater than 1, the block chooses a filter architecture that results in the fewest multipliers. If N allows for a single multiplier in each subfilter, then the block implements a single serial filter and decimates the output samples.
Direct form transposed— This architecture is a fully parallel implementation that is suitable for FPGA and ASIC applications.
All implementations share resources by interleaving the subfilter coefficients over one filter implementation for each sample in the input vector.
The block implements a polyphase decomposition filter using Discrete FIR Filter blocks. For architecture details, see FIR Filter Architectures for FPGAs and ASICs.
Specify an integer decimation factor greater than two. When you use vector input and the vector size is less than the decimation factor, the decimation factor must be an integer multiple of the vector size. When you use vector input and the vector size is greater than the decimation factor, the vector size must be an integer multiple of the decimation factor.
Serialization requirement for input timing, specified as a
positive integer. This parameter represents
N, the minimum number of cycles
between valid input samples. To implement a fully serial
architecture, set Minimum number of cycles
between valid input samples greater than
the filter length, L, or to
Inf.
The block applies coefficient optimizations before serialization, so the sharing factor of the final filter can be lower than the number of cycles that you specified.
Dependencies
To enable this parameter, set Filter
structure to Direct form
systolic.
You cannot use frame-based input with Minimum number of cycles between valid input samples greater than 1.
Since R2024b
Enable sharing multipliers across symmetric coefficients in the polyphase filter architecture. This optimization reduces latency and halves the number of multipliers.
Polyphase decomposition of symmetric filter coefficients
does not result in symmetry in each polyphase branch. For
example, if the filter coefficients are [1 2 3 4
4 3 2 1], after decomposition the two
polyphase branches are [1 3 4 2] and
[2 4 3 1]. Symmetric pairs
optimization refactors the coefficients to restore
symmetry on the polyphase branches. The implementation
includes a pre-adder to combine input samples for the
refactored polyphase branches. The filter output is the
same as the output of the non-optimized implementation.
Data Types
Rounding mode for type-casting the output to the data type specified by the Output parameter. When the input data type is floating point, the block ignores this parameter. For more details, see Rounding Modes.
Overflow handling for type-casting the output to the data type specified by the Output parameter. When the input data type is floating point, the block ignores this parameter. For more details, see Overflow Handling.
When the input is a fixed-point or integer type, the block casts the filter coefficients using the rule or data type in this parameter. The quantization rounds to the nearest representable value and saturates on overflow. When the input data type is a floating-point type, the block ignores this parameter and all internal arithmetic uses the same data type as the input.
The recommended data type for this parameter is
Inherit: Same word length as
input.
The block returns a warning or error if:
The coefficients data type does not have enough fractional length to represent the coefficients accurately.
The coefficients data type is unsigned, and the coefficients include negative values.
When the input is a fixed-point or integer type, the block casts the output of the filter using the rule or data type in this parameter. The quantization uses the settings of the Rounding mode and Overflow mode parameters. When the input data type is floating point, the block ignores this parameter and returns output in the same data type as the input.
The block increases the word length for full precision inside each filter tap and casts the final output to the specified type. The maximum final internal data type (WF) depends on the input data type (WI), the coefficient data type (WC), and the number of coefficients (L) and is given by
WF = WI +
WC +
ceil(log2(L)).
Because the coefficient values limit the potential growth, usually the actual full-precision internal word length is smaller than WF.
Control Ports
Select this check box to enable the reset input port. The reset signal implements a local synchronous reset of the data path registers.
For more reset considerations, see the Reset Signal section on the Hardware Control Signals page.
Select this check box to connect the generated HDL global reset signal to the data path registers. This parameter does not change the appearance of the block or modify simulation behavior in Simulink. When you clear this check box, the generated HDL global reset clears only the control path registers. The generated HDL global reset can be synchronous or asynchronous depending on the HDL Code Generation > Global Settings > Reset type parameter in the model Configuration Parameters.
For more reset considerations, see the Reset Signal section on the Hardware Control Signals page.
Algorithms
The block implements a polyphase filter bank where the filter coefficients are decomposed into DecimationFactor subfilters. If the filter length is not divisible by the Decimation factor parameter value, then the block zero-pads the coefficients. When your input is regularly spaced, with two or more cycles between valid samples, as indicated by the Minimum number of cycles between valid input samples parameter, the filter can share multiplier resources in time.
This flow chart shows which filter architectures result from your parameter settings. It also shows the number of multipliers used by the filter implementation. The filter architecture depends on the input frame size, V, the decimation factor, R, the number of cycles between valid input samples, N, and the number of filter coefficients, L. The architectures are in order from lowest resource use on the left, to higher resources on the right. The higher resource architectures are trading off resource use for higher throughput. Each architecture is described below the flow chart.
If the filter is symmetric and you select
Optimize symmetric coefficients, the architecture
shares multipliers for matching coefficients, so effectively
L =
L/2. (since R2024b)
The number of multipliers shown in the flow chart is for filters with real input and real coefficients. For complex input, the filter uses three times as many multipliers.

Architecture 1 — Fully parallel one-tap interleaved polyphase filter bank.
When DecimationFactor is greater than the filter length, for any value of NumCycles, the filter becomes a single-tap fully parallel systolic filter with interleaved coefficients, and uses a single multiplier.
For this architecture, the latency displayed on the block is the number of cycles between the first valid input and the first valid output, assuming the input is contiguous. The latency is longer than displayed if there are invalid cycles between valid input samples, because the fully parallel systolic filter requires new valid input samples to advance the pipeline.
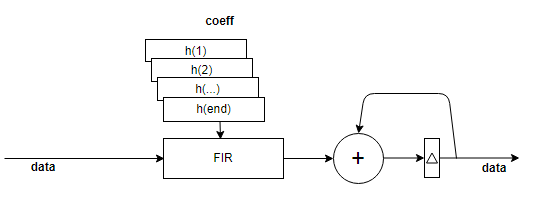
Architecture 2 — Single fully serial filter.
When the filter has NumCycles greater than the number of filter coefficients, the block implements a single fully serial filter and decimates the output samples by the decimation factor. This serial filter uses one multiplier.
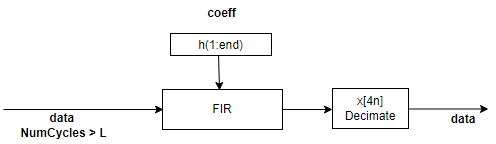
Architecture 3 — Partly serial polyphase filter bank.
When the filter has NumCycles greater than one and less than the number of filter coefficients, the block implements a polyphase filter with DecimationFactor subfilters. This diagram shows input data with a valid sample every second cycle and a DecimationFactor of
4. The output data has one valid sample every eight cycles. This filter implementation uses FilterLength/NumCycles multipliers.
Architecture 4 — Fully parallel polyphase interleaved filter bank (scalar).
The diagram shows the polyphase filter bank with scalar input, DecimationFactor set to
4, and NumCycles set to1. The four sets of decomposed coefficients are interleaved in time over a single subfilter. The output data sample is valid every four cycles. The filter uses FilterLength/DecimationFactor multipliers.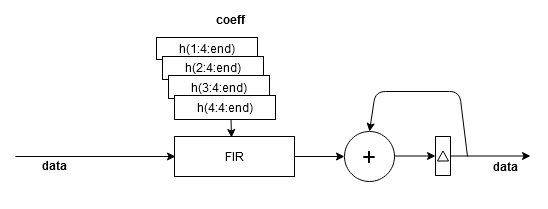
Architecture 5 — Fully parallel polyphase interleaved filter bank (vector)
The diagram shows the polyphase filter bank for an input vector size smaller than the decimation factor. This filter has an input vector of four values and DecimationFactor is set to 8. Each of the four subfilters has two sets of coefficients interleaved in time. The filter uses InputSize*FilterLength/DecimationFactor multipliers.

Architecture 6 — Fully parallel frame-based filter bank
With an input vector size greater than the decimation factor, the block implements decimation factor subfilters, each with frame-based input of VectorSize/DecimationFactor samples. The output vector has VectorSize/DecimationFactor samples. The filter uses InputSize*FilterLength/DecimationFactor multipliers.
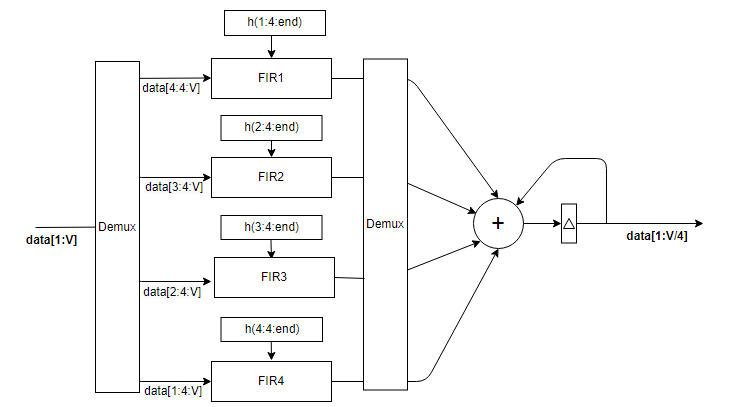
Each subfilter is implemented with a Discrete FIR Filter block. The adder at the output is pipelined to accommodate higher synthesis frequencies. For architecture details, see FIR Filter Architectures for FPGAs and ASICs.
Note
The output of the FIR Decimator block does not match the output of the FIR Decimation block from DSP System Toolbox™ sample-for-sample. This difference is mainly because of the phase in which the samples are applied across the subfilters. To match the FIR Decimation block, apply Decimation factor – 1 zeros to the FIR Decimator block at the start of the data stream.
The FIR Decimation block also uses slightly different data types for full-precision calculations. The different data types can also introduce differences in output values if the values overflow the internal data types.
This table shows the post-synthesis resource utilization for the HDL code
generated for the default FIR decimation filter using scalar input, a
decimation factor of eight, 16-bit input, and 16-bit coefficients. The
synthesis targets a Xilinx ZC-706 (XC7Z045ffg900-2) FPGA. The Global HDL reset
type parameter is Synchronous,
and the Minimize clock enables parameter is selected.
The reset port is disabled, so only the control path
registers are connected to the generated global HDL reset.
| Resource | Uses |
|---|---|
| LUT | 676 |
| Slice Reg | 878 |
| Slice | 257 |
| Xilinx LogiCORE DSP48 | 5 |
After place and route, the maximum clock frequency of the design is 526 MHz.
For the same filter with a four-element input vector, the filter uses these resources.
| Resource | Uses |
|---|---|
| LUT | 322 |
| Slice Reg | 2351 |
| Slice | 502 |
| Xilinx LogiCORE DSP48 | 20 |
After place and route, the maximum clock frequency of the design is 518 MHz.
For the same filter with scalar input and numCycles set to four, the filter uses these resources.
| Resource | Uses |
|---|---|
| LUT | 835 |
| Slice Reg | 1341 |
| Xilinx LogiCORE DSP48 | 8 |
After place and route, the maximum clock frequency of the design is 460 MHz.
Extended Capabilities
This block supports C/C++ code generation for Simulink accelerator and rapid accelerator modes and for DPI component generation.
HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.
| ConstrainedOutputPipeline | Number of registers to place at
the outputs by moving existing delays within your design. Distributed
pipelining does not redistribute these registers. The default is
|
| InputPipeline | Number of input pipeline stages
to insert in the generated code. Distributed pipelining and constrained
output pipelining can move these registers. The default is
|
| OutputPipeline | Number of output pipeline stages
to insert in the generated code. Distributed pipelining and constrained
output pipelining can move these registers. The default is
|
The FIR Decimator block does not support resource sharing optimization
through HDL Coder settings. Instead, set the Filter
structure parameter to Partly serial
systolic, and configure a serialization factor
based on either input timing or resource usage.
Version History
Introduced in R2020bThe block provides an optional coeff port to allow
coefficient changes at any time. Set the Coefficient
source parameter to Input port (Parallel
interface), and specify the filter coefficients as a row
vector of real or complex values.
You can set the Coefficients prototype property to indicate the locations of consistently zero-valued coefficients, such as, if all input coefficients are half-band filters. When given a prototype, the block removes multipliers for zero-valued coefficients.
Use the Optimize symmetric coefficients parameter to enable optimizing symmetric coefficient multipliers in the polyphase filter architecture. This optimization reduces latency and halves the number of multipliers.
Before R2022a, this block was named FIR Decimation HDL Optimized and was included in the DSP System Toolbox DSP System Toolbox HDL Support library.
This block supports partly and fully serial systolic architecture. This
architecture enables you to share hardware resources if there is a regular
pattern of invalid cycles between valid input samples. To use the serial
systolic architecture, set Filter structure to
Direct form systolic and Minimum
number of cycles between valid input samples to a value
greater than 1. You cannot use frame-based input with the serial
architecture.
In previous releases, the block did not support input vector sizes greater than the decimation factor.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)

