Evaluate Lane Boundary Detections Against Ground Truth Data
This example shows how to compare ground truth data against results of a lane boundary detection algorithm. It also illustrates how this comparison can be used to tune algorithm parameters to get the best detection results.
Overview
Ground truth data is usually available in image coordinates, whereas boundaries are modeled in the vehicle coordinate system. Comparing the two involves a coordinate conversion and thus requires extra care in interpreting the results. Driving decisions are based on distances in the vehicle coordinate system. Therefore, it is more useful to express and understand accuracy requirements using physical units in the vehicle coordinates rather than pixel coordinates.
The Visual Perception Using Monocular Camera describes the internals of a monocular camera sensor and the process of modeling lane boundaries. This example shows how to evaluate the accuracy of these models against manually validated ground truth data. After establishing a comparison framework, the framework is extended to fine-tune parameters of a boundary detection algorithm for optimal performance.
Load and Prepare Ground Truth Data
You can use the Ground Truth Labeler app to mark and label lane boundaries in a video. These annotated lane boundaries are represented as sets of points placed along the boundaries of interest. Having a rich set of manually annotated lane boundaries for various driving scenarios is critical in evaluating and fine-tuning automatic lane boundary detection algorithms. An example set for the caltech_cordova1.avi video file is available with the toolbox.
Load predefined left and right ego lane boundaries specified in image coordinates. Each boundary is represented by a set of M-by-2 numbers representing M pixel locations along that boundary. Each video frame has at most two such sets representing the left and the right lane.
loaded = load('caltech_cordova1_EgoBoundaries.mat'); sensor = loaded.sensor; % Associated monoCamera object gtImageBoundaryPoints = loaded.groundTruthData.EgoLaneBoundaries; % Show a sample of the ground truth at this frame index frameInd = 36; % Load the video frame frameTimeStamp = seconds(loaded.groundTruthData(frameInd,:).Time); videoReader = VideoReader(loaded.videoName); videoReader.CurrentTime = frameTimeStamp; frame = videoReader.readFrame(); % Obtain the left lane points for this frame boundaryPoints = gtImageBoundaryPoints{frameInd}; leftLanePoints = boundaryPoints{1}; figure imshow(frame) hold on plot(leftLanePoints(:,1), leftLanePoints(:,2),'+','MarkerSize',10,'LineWidth',4); title('Sample Ground Truth Data for Left Lane Boundary');

Convert the ground truth points from image coordinates to vehicle coordinates to allow for direct comparison with boundary models. To perform this conversion, use the imageToVehicle function with the associated monoCamera object to perform this conversion.
gtVehicleBoundaryPoints = cell(numel(gtImageBoundaryPoints),1); for frameInd = 1:numel(gtImageBoundaryPoints) boundaryPoints = gtImageBoundaryPoints{frameInd}; if ~isempty(boundaryPoints) ptsInVehicle = cell(1, numel(boundaryPoints)); for cInd = 1:numel(boundaryPoints) ptsInVehicle{cInd} = imageToVehicle(sensor, boundaryPoints{cInd}); end gtVehicleBoundaryPoints{frameInd} = ptsInVehicle; end end
Model Lane Boundaries Using a Monocular Sensor
Run a lane boundary modeling algorithm on the sample video to obtain the test data for the comparison. Here, reuse the helperMonoSensor module introduced in the Visual Perception Using Monocular Camera example. While processing the video, an additional step is needed to return the detected boundary models. This logic is wrapped in a helper function, detectBoundaries, defined at the end of this example.
monoSensor = helperMonoSensor(sensor); boundaries = detectBoundaries(loaded.videoName, monoSensor);
Evaluate Lane Boundary Models
Use the evaluateLaneBoundaries function to find the number of boundaries that match those boundaries in ground truth. A ground truth is assigned to a test boundary only if all points of the ground truth are within a specified distance, laterally, from the corresponding test boundary. If multiple ground truth boundaries satisfy this criterion, the one with the smallest maximum lateral distance is chosen. The others are marked as false positives.
threshold = 0.25; % in vehicle coordinates (meters) [numMatches, numMisses, numFalsePositives, assignments] = ... evaluateLaneBoundaries(boundaries, gtVehicleBoundaryPoints, threshold); disp(['Number of matches: ', num2str(numMatches)]);
Number of matches: 408
disp(['Number of misses: ', num2str(numMisses)]);Number of misses: 37
disp(['Number of false positives: ', num2str(numFalsePositives)]);Number of false positives: 27
You can use these raw counts to compute other statistics such as precision, recall, and the F1 score:
precision = numMatches/(numMatches+numFalsePositives);
disp(['Precision: ', num2str(precision)]);Precision: 0.93793
recall = numMatches/(numMatches+numMisses);
disp(['Sensitivity/Recall: ', num2str(recall)]);Sensitivity/Recall: 0.91685
f1Score = 2*(precision*recall)/(precision+recall);
disp(['F1 score: ', num2str(f1Score)]);F1 score: 0.92727
Visualize Results Using a Bird's-Eye Plot
evaluateLaneBoundaries additionally returns the assignment indices for every successful match between the ground truth and test boundaries. This can be used to visualize the detected and ground truth boundaries to gain a better understanding of failure modes.
Find a frame that has one matched boundary and one false positive. The ground truth data for each frame has two boundaries. So, a candidate frame will have two assignment indices, with one of them being 0 to indicate a false positive.
hasMatch = cellfun(@(x)numel(x)==2, assignments);
hasFalsePositive = cellfun(@(x)nnz(x)==1, assignments);
frameInd = find(hasMatch&hasFalsePositive,1,'first');
frameVehiclePoints = gtVehicleBoundaryPoints{frameInd};
frameImagePoints = gtImageBoundaryPoints{frameInd};
frameModels = boundaries{frameInd};Use the assignments output of evaluateLaneBoundaries to find the models that matched (true positives) and models that had no match (false positives) in ground truth.
matchedModels = frameModels(assignments{frameInd}~=0);
fpModels = frameModels(assignments{frameInd}==0);Set up a bird's-eye plot and visualize the ground truth points and models on it.
bep = birdsEyePlot(); gtPlotter = laneBoundaryPlotter(bep,'DisplayName','Ground Truth',... 'Color','blue'); tpPlotter = laneBoundaryPlotter(bep,'DisplayName','True Positive',... 'Color','green'); fpPlotter = laneBoundaryPlotter(bep,'DisplayName','False Positive',... 'Color','red'); plotLaneBoundary(gtPlotter, frameVehiclePoints); plotLaneBoundary(tpPlotter, matchedModels); plotLaneBoundary(fpPlotter, fpModels);

title('Bird''s-Eye Plot of Comparison Results');
Visualize Results on a Video in Camera and Bird's-Eye View
To get a better context of the result, you can also visualize ground truth points and the boundary models on the video.
Get the frame corresponding to the frame of interest.
videoReader = VideoReader(loaded.videoName); videoReader.CurrentTime = seconds(loaded.groundTruthData.Time(frameInd)); frame = videoReader.readFrame();
Consider the boundary models as a solid line (irrespective of how the sensor classifies it) for visualization.
fpModels.BoundaryType = 'Solid'; matchedModels.BoundaryType = 'Solid';
Insert the matched models, false positives and the ground truth points. This plot is useful in deducing that the presence of crosswalks poses a challenging scenario for the boundary modeling algorithm.
xVehicle = 3:20; frame = insertLaneBoundary(frame, fpModels, sensor, xVehicle,'Color','Red'); frame = insertLaneBoundary(frame, matchedModels, sensor, xVehicle,'Color','Green'); figure ha = axes; imshow(frame,'Parent', ha); % Combine the left and right boundary points boundaryPoints = [frameImagePoints{1};frameImagePoints{2}]; hold on plot(ha, boundaryPoints(:,1), boundaryPoints(:,2),'+','MarkerSize',10,'LineWidth',4); title('Camera View of Comparison Results');

You can also visualize the results in the bird's-eye view of this frame.
birdsEyeImage = transformImage(monoSensor.BirdsEyeConfig,frame); xVehicle = 3:20; birdsEyeImage = insertLaneBoundary(birdsEyeImage, fpModels, monoSensor.BirdsEyeConfig, xVehicle,'Color','Red'); birdsEyeImage = insertLaneBoundary(birdsEyeImage, matchedModels, monoSensor.BirdsEyeConfig, xVehicle,'Color','Green'); % Combine the left and right boundary points ptsInVehicle = [frameVehiclePoints{1};frameVehiclePoints{2}]; gtPointsInBEV = vehicleToImage(monoSensor.BirdsEyeConfig, ptsInVehicle); figure imshow(birdsEyeImage); hold on plot(gtPointsInBEV(:,1), gtPointsInBEV(:,2),'+','MarkerSize', 10,'LineWidth',4); title('Bird''s-Eye View of Comparison Results');

Tune Boundary Modeling Parameters
You can use the evaluation framework described previously to fine-tune parameters of the lane boundary detection algorithm. helperMonoSensor exposes three parameters that control the results of the lane-finding algorithm.
LaneSegmentationSensitivity- Controls the sensitivity ofsegmentLaneMarkerRidgefunction. This function returns lane candidate points in the form of a binary lane feature mask. The sensitivity value can vary from 0 to 1, with a default of 0.25. Increasing this number results in more lane candidate points and potentially more false detections.LaneXExtentThreshold- Specifies the minimum extent (length) of a lane. It is expressed as a ratio of the detected lane length to the maximum lane length possible for the specified camera configuration. The default value is 0.4. Increase this number to reject shorter lane boundaries.LaneStrengthThreshold- Specifies the minimum normalized strength to accept a detected lane boundary.
LaneXExtentThreshold and LaneStrengthThreshold are derived from the XExtent and Strength properties of the parabolicLaneBoundary object. These properties are an example of how additional constraints can be placed on the boundary modeling algorithms to obtain acceptable results. The impact of varying LaneStrengthThreshold has additional nuances worth exploring. Typical lane boundaries are marked with either solid or dashed lines. When comparing to solid lines, dashed lines have a lower number of inlier points, leading to lower strength values. This makes it challenging to set a common strength threshold. To inspect the impact of this parameter, first generate all boundaries by setting LaneStrengthThreshold to 0. This setting ensures it has no impact on the output.
monoSensor.LaneStrengthThreshold = 0;
boundaries = detectBoundaries('caltech_cordova1.avi', monoSensor);The LaneStrengthThreshold property of helperMonoSensor controls the normalized Strength parameter of each parabolicLaneBoundary model. The normalization factor, MaxLaneStrength, is the strength of a virtual lane that runs for the full extent of a bird's-eye image. This value is determined solely by the birdsEyeView configuration of helperMonoSensor. To assess the impact of LaneStrengthThreshold, first compute the distribution of the normalized lane strengths for all detected boundaries in the sample video. Note the presence of two clear peaks, one at a normalized strength of 0.3 and one at 0.7. These two peaks correspond to dashed and solid lane boundaries respectively. From this plot, you can empirically determine that to ensure dashed lane boundaries are detected, LaneStrengthThreshold should be below 0.3.
strengths = cellfun(@(b)[b.Strength], boundaries,'UniformOutput',false); strengths = [strengths{:}]; normalizedStrengths = strengths/monoSensor.MaxLaneStrength; figure; hist(normalizedStrengths); title('Histogram of Normalized Lane Strengths');
You can use the comparison framework to further assess the impact of the LaneStrengthThreshold parameters on the detection performance of the modeling algorithm. Note that the threshold value controlling the maximum physical distance between a model and a ground truth remains the same as before. This value is dictated by the accuracy requirements of an ADAS system and usually does not change.
threshold = .25;
[~, ~, ~, assignments] = ...
evaluateLaneBoundaries(boundaries, gtVehicleBoundaryPoints, threshold);Bin each boundary according to its normalized strength. The assignments information helps classify each boundary as either a true positive (matched) or a false positive. LaneStrengthThreshold is a "min" threshold, so a boundary classified as a true positive at a given value will continue to be a true positive for all lower threshold values.
nMatch = zeros(1,100); % Normalized lane strength is bucketed into 100 bins nFP = zeros(1,100); % ranging from 0.01 to 1.00. for frameInd = 1:numel(boundaries) frameBoundaries = boundaries{frameInd}; frameAssignment = assignments{frameInd}; for bInd = 1:numel(frameBoundaries) normalizedStrength = frameBoundaries(bInd).Strength/monoSensor.MaxLaneStrength; strengthBucket = floor(normalizedStrength*100); if frameAssignment(bInd) % This boundary was matched with a ground truth boundary, % record as a true positive for all values of strength above % its strength value. nMatch(1:strengthBucket) = nMatch(1:strengthBucket)+1; else % This is a false positive nFP(1:strengthBucket) = nFP(1:strengthBucket)+1; end end end
Use this information to compute the number of "missed" boundaries, that is, ground truth boundaries that the algorithm failed to detect at the specified LaneStrengthThreshold value. And with that information, compute the precision and recall metrics.
gtTotal = sum(cellfun(@(x)numel(x),gtVehicleBoundaryPoints)); nMiss = gtTotal - nMatch; precisionPlot = nMatch./(nMatch + nFP); recallPlot = nMatch./(nMatch + nMiss);
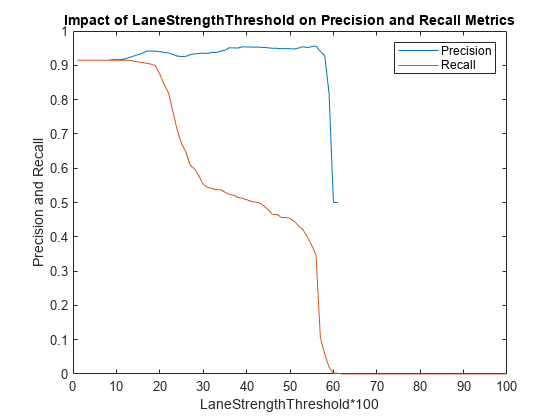
Plot the precision and recall metrics against various values of the lane strength threshold parameter. This plot is useful in determining an optimal value for the lane strength parameter. For this video clip, to maximize recall and precision metrics, LaneStrengthThreshold should be in the range 0.20 - 0.25.
figure; plot(precisionPlot); hold on; plot(recallPlot); xlabel('LaneStrengthThreshold*100'); ylabel('Precision and Recall'); legend('Precision','Recall'); title('Impact of LaneStrengthThreshold on Precision and Recall Metrics');

Supporting Function
Detect boundaries in a video.
detectBoundaries uses a preconfigured helperMonoSensor object to detect boundaries in a video.
function boundaries = detectBoundaries(videoName, monoSensor) videoReader = VideoReader(videoName); hwb = waitbar(0,'Detecting and modeling boundaries in video...'); closeBar = onCleanup(@()delete(hwb)); frameInd = 0; boundaries = {}; while hasFrame(videoReader) frameInd = frameInd+1; frame = readFrame(videoReader); sensorOut = processFrame(monoSensor, frame); % Save the boundary models boundaries{end+1} =... [sensorOut.leftEgoBoundary, sensorOut.rightEgoBoundary]; %#ok<AGROW> waitbar(frameInd/(videoReader.Duration*videoReader.FrameRate), hwb); end end