Sequence-to-Sequence Classification Using 1-D Convolutions
This example shows how to classify each time step of sequence data using a generic temporal convolutional network (TCN).
While sequence-to-sequence tasks are commonly solved with recurrent neural network architectures, Bai et al. [1] show that convolutional neural networks can match the performance of recurrent networks on typical sequence modeling tasks or even outperform them. Potential benefits of using convolutional networks are better parallelism, better control over the receptive field size, better control of the memory footprint of the network during training, and more stable gradients. Just like recurrent networks, convolutional networks can operate on variable length input sequences and can be used to model sequence-to-sequence or sequence-to-one tasks.
In this example, you train a TCN to recognize the activity of person wearing a smartphone on the body. You train the network using time series data representing accelerometer readings in three directions.
Load Training Data
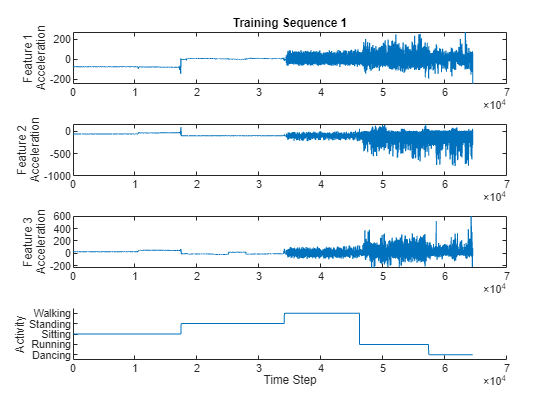
Load the Human Activity Recognition data. The data contains seven time series of sensor data obtained from a smartphone worn on the body. Each sequence has three features and varies in length. The three features correspond to accelerometer readings in three directions.
s = load("HumanActivityTrain.mat");
XTrain = s.XTrain;
TTrain = s.YTrain;View the number of observations in the training data.
numObservations = numel(XTrain)
numObservations = 6
View the number of classes in the training data.
classes = categories(TTrain{1});
numClasses = numel(classes)numClasses = 5
View the number of features of the training data.
numFeatures = size(s.XTrain{1},1)numFeatures = 3
Visualize one of the training sequences in a plot. Plot the features of the first training sequence and the corresponding activity.
figure for i = 1:3 X = s.XTrain{1}(i,:); subplot(4,1,i) plot(X) ylabel("Feature " + i + newline + "Acceleration") end subplot(4,1,4) hold on plot(s.YTrain{1}) hold off xlabel("Time Step") ylabel("Activity") subplot(4,1,1) title("Training Sequence 1")
Define Deep Learning Model
The main building block of a TCN is a dilated causal convolution layer, which operates over the time steps of each sequence. In this context, "causal" means that the activations computed for a particular time step cannot depend on activations from future time steps.
To build up context from previous time steps, multiple convolutional layers are typically stacked on top of each other. To achieve large receptive field sizes, the dilation factor of subsequent convolution layers is increased exponentially, as shown in the following image. Assuming that the dilation factor of the k-th convolutional layer is and the stride is 1, then the receptive field size of such a network can be computed as , where is the filter size and is the number of convolutional layers. Change the filter size and number of layers to easily adjust the receptive field size and the number of learnable parameters as necessary for the data and task at hand.
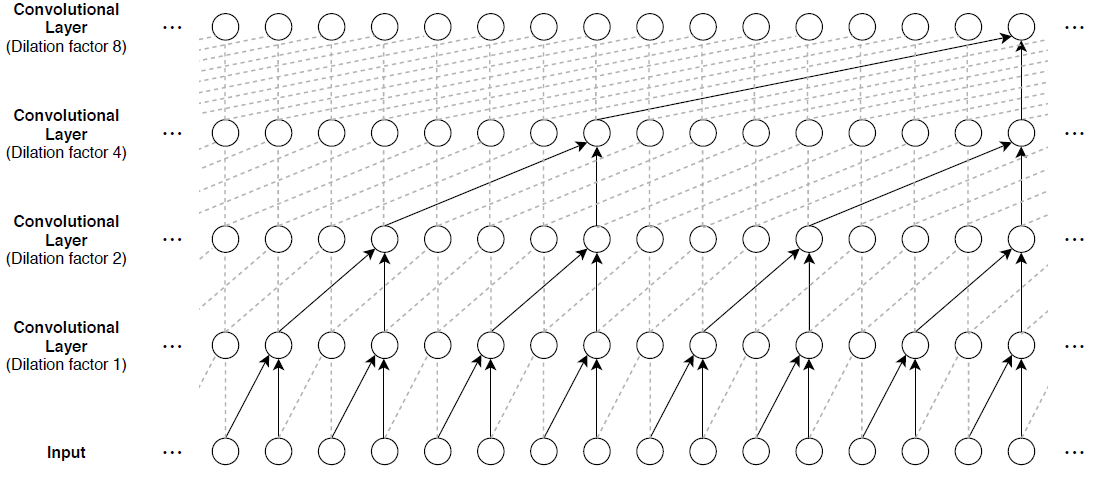
One of the disadvantages of TCNs compared to recurrent networks is that they have a larger memory footprint during inference. The entire raw sequence is required to compute the next time step. To reduce inference time and memory consumption, especially for step-ahead predictions, train with the smallest sensible receptive field size and perform prediction only with the last time steps of the input sequence.
The general TCN architecture (as described in [1]) consists of multiple residual blocks, each containing two sets of dilated causal convolution layers with the same dilation factor, followed by normalization, ReLU activation, and spatial dropout layers. The network adds the input of each block to the output of the block (including a 1-by-1 convolution on the input when the number of channels between the input and output do not match) and applies a final activation function.

Define a network containing four of these residual blocks in series, each with double the dilation factor of the previous layer, starting with a dilation factor of 1. For the residual blocks, specify 64 filters for the 1-D convolutional layers with a filter size of 5 and a dropout factor of 0.005 for the spatial dropout layers.
You can also build this network using the Deep Network Designer app. On the Deep Network Designer Start Page, in the Sequence-to-Sequence Classification Networks (Untrained) section, click TCN.
numFilters = 64; filterSize = 5; dropoutFactor = 0.005; numBlocks = 4; net = dlnetwork; layer = sequenceInputLayer(numFeatures,Normalization="rescale-symmetric",Name="input"); net = addLayers(net,layer); outputName = layer.Name; for i = 1:numBlocks dilationFactor = 2^(i-1); layers = [ convolution1dLayer(filterSize,numFilters,DilationFactor=dilationFactor,Padding="causal",Name="conv1_"+i) layerNormalizationLayer spatialDropoutLayer(Probability=dropoutFactor) convolution1dLayer(filterSize,numFilters,DilationFactor=dilationFactor,Padding="causal") layerNormalizationLayer reluLayer spatialDropoutLayer(Probability=dropoutFactor) additionLayer(2,Name="add_"+i)]; % Add and connect layers. net = addLayers(net,layers); net = connectLayers(net,outputName,"conv1_"+i); % Skip connection. if i == 1 % Include convolution in first skip connection. layer = convolution1dLayer(1,numFilters,Name="convSkip"); net = addLayers(net,layer); net = connectLayers(net,outputName,"convSkip"); net = connectLayers(net,"convSkip","add_" + i + "/in2"); else net = connectLayers(net,outputName,"add_" + i + "/in2"); end % Update layer output name. outputName = "add_" + i; end layers = [ fullyConnectedLayer(numClasses,Name="fc") softmaxLayer]; net = addLayers(net,layers); net = connectLayers(net,outputName,"fc");
View the network in a plot.
figure
plot(net)
title("Temporal Convolutional Network")
Specify Training Options
Specify a set of options used for training. Choosing among the options requires empirical analysis. To explore different training option configurations by running experiments, you can use the Experiment Manager app.
Train using the Adam optimizer.
Train for 60 epochs with a mini-batch size of 1.
Because the training data has sequences with rows and columns corresponding to channels and time steps, respectively, specify the input data format
"CTB"(channel, time, batch).Display the training progress in a plot and monitor the accuracy.
Disable the verbose output.
options = trainingOptions("adam", ... MaxEpochs=60, ... miniBatchSize=1, ... InputDataFormats="CTB", ... Plots="training-progress", ... Metrics="accuracy", ... Verbose=0);
Train Model
Train the neural network using the trainnet function. By default, the trainnet function uses a GPU if one is available. Training on a GPU requires a Parallel Computing Toolbox™ license and a supported GPU device. For information on supported devices, see GPU Computing Requirements (Parallel Computing Toolbox). Otherwise, the trainnet function uses the CPU. To specify the execution environment, use the ExecutionEnvironment training option.
net = trainnet(XTrain,TTrain,net,"crossentropy",options);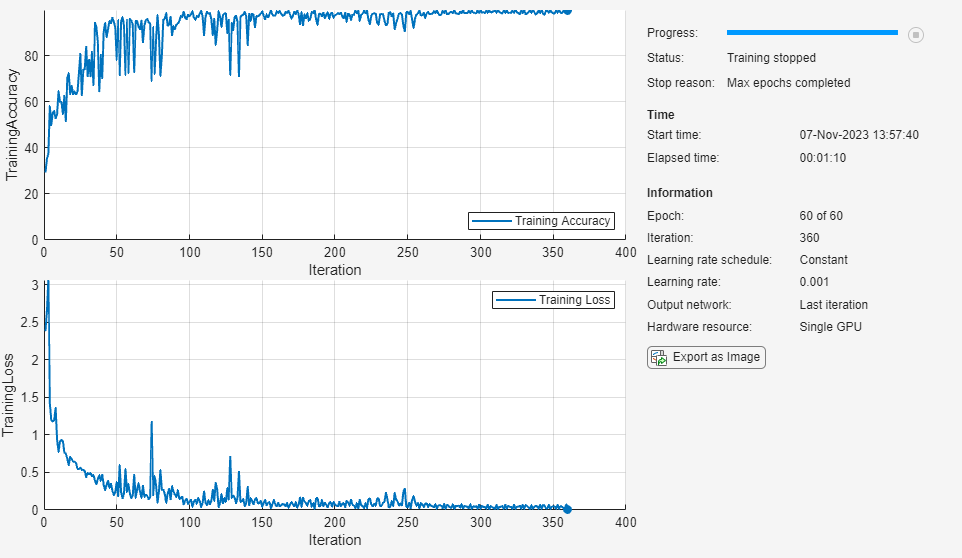
Test Model
Test the classification accuracy of the model by comparing the predictions on a held-out test set with the true labels for each time step.
Load the test data.
s = load("HumanActivityTest.mat");
XTest = s.XTest;
TTest = s.YTest;Classify the test images. To make predictions with multiple observations, use the minibatchpredict function. To convert the prediction scores to labels, use the scores2label function. The minibatchpredict function automatically uses a GPU if one is available. Otherwise, the function uses the CPU.
scores = minibatchpredict(net,XTest,InputDataFormats="CTB");
YPred = scores2label(scores,classes);Compare the predictions with the corresponding test data in a plot.
figure plot(YPred,".-") hold on plot(TTest{1}) hold off xlabel("Time Step") ylabel("Activity") legend(["Predicted" "Test Data"],Location="northeast") title("Test Sequence Predictions")
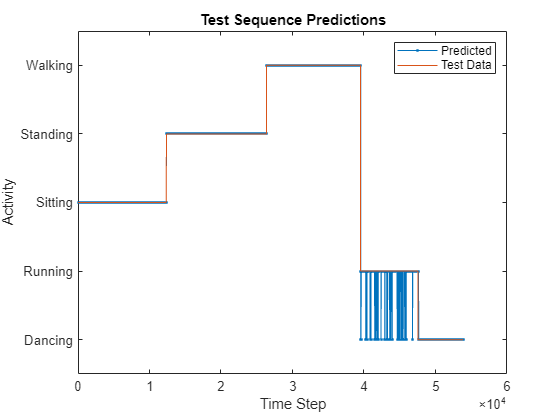
Visualize the predictions in a confusion matrix.
figure
confusionchart(TTest{1},YPred)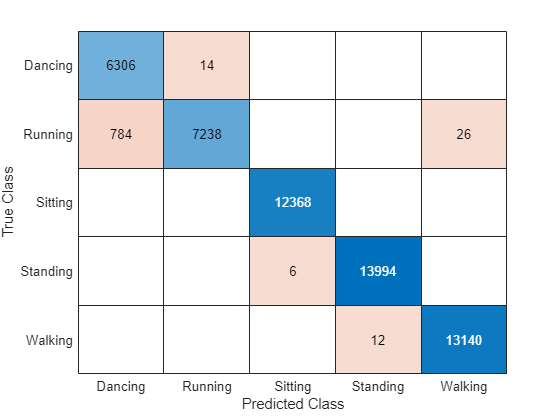
Evaluate the classification accuracy by comparing the predictions to the test labels.
accuracy = mean(YPred == TTest{1})accuracy = 0.9905
References
[1] Bai, Shaojie, J. Zico Kolter, and Vladlen Koltun. “An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling.” Preprint, submitted April 19, 2018. https://arxiv.org/abs/1803.01271.
[2] Oord, Aaron van den, Sander Dieleman, Heiga Zen, Karen Simonyan, Oriol Vinyals, Alex Graves, Nal Kalchbrenner, Andrew Senior, and Koray Kavukcuoglu. “WaveNet: A Generative Model for Raw Audio.” Preprint, submitted September 12, 2016. https://arxiv.org/abs/1609.03499.
[3] Tompson, Jonathan, Ross Goroshin, Arjun Jain, Yann LeCun, and Christoph Bregler. “Efficient Object Localization Using Convolutional Networks.” 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 648–56. https://doi.org/10.1109/CVPR.2015.7298664.
See Also
convolution1dLayer | trainnet | trainingOptions | dlnetwork | sequenceInputLayer | maxPooling1dLayer | averagePooling1dLayer | globalMaxPooling1dLayer | globalAveragePooling1dLayer
Topics
- Sequence Classification Using 1-D Convolutions
- Sequence Classification Using Deep Learning
- Sequence-to-Sequence Classification Using Deep Learning
- Sequence-to-Sequence Regression Using Deep Learning
- Sequence-to-One Regression Using Deep Learning
- Time Series Forecasting Using Deep Learning
- Long Short-Term Memory Neural Networks
- List of Deep Learning Layers
- Deep Learning Tips and Tricks