Sequence-to-One Regression Using Deep Learning
This example shows how to predict the frequency of a waveform using a long short-term memory (LSTM) neural network.
You can use an LSTM neural network to predict a numeric response of a sequence using a training set of sequences and target values. An LSTM network is a recurrent neural network (RNN) that processes input data by looping over time steps and updating the network state. The network state contains information remembered over previous time steps. Examples of numeric responses of a sequence include:
Properties of the sequence, such as its frequency, maximum value, and mean.
Values of past or future time steps of the sequence.
This example trains a sequence-to-one regression LSTM network using the Waveform data set, which contains 1000 synthetically generated waveforms of varying lengths with three channels. To determine the frequency of a waveform using conventional methods, see fft.
Load Sequence Data
Load the example data from WaveformData.mat. The data is a numObservations-by-1 cell array of sequences, where numObservations is the number of sequences. Each sequence is a numTimeSteps-by-numChannels numeric array, where numTimeSteps is the number of time steps in the sequence and numChannels is the number of channels of the sequence. The corresponding targets are in a numObservations-by-numResponses numeric array of the frequencies of the waveforms, where numResponses is the number of channels of the targets.
load WaveformDataView the number of observations.
numObservations = numel(data)
numObservations = 1000
View the sizes of the first few sequences and the corresponding frequencies.
data(1:4)
ans=4×1 cell array
{103×3 double}
{136×3 double}
{140×3 double}
{124×3 double}
freq(1:4,:)
ans = 4×1
5.8922
2.2557
4.5250
4.4418
View the number of channels of the sequences. For network training, each sequence must have the same number of channels.
numChannels = size(data{1},2)numChannels = 3
View the number of responses (the number of channels of the targets).
numResponses = size(freq,2)
numResponses = 1
Visualize the first few sequences in plots.
figure tiledlayout(2,2) for i = 1:4 nexttile stackedplot(data{i}, DisplayLabels="Channel " + (1:numChannels)) xlabel("Time Step") title("Frequency: " + freq(i)) end
Prepare Data for Training
Set aside data for validation and testing. Partition the data into a training set containing 80% of the data, a validation set containing 10% of the data, and a test set containing the remaining 10% of the data.
[idxTrain,idxValidation,idxTest] = trainingPartitions(numObservations, [0.8 0.1 0.1]); XTrain = data(idxTrain); XValidation = data(idxValidation); XTest = data(idxTest); TTrain = freq(idxTrain); TValidation = freq(idxValidation); TTest = freq(idxTest);
Define LSTM Network Architecture
Create an LSTM regression network.
Use a sequence input layer with an input size that matches the number of channels of the input data.
For a better fit and to prevent the training from diverging, set the
Normalizationoption of the sequence input layer to "zscore". This normalizes the sequence data to have zero mean and unit variance.Use an LSTM layer with 100 hidden units. The number of hidden units determines how much information is learned by the layer. Larger values can yield more accurate results but can be more susceptible to overfitting to the training data.
To output a single time step for each sequence, set the
OutputModeoption of the LSTM layer to "last".To specify the number of values to predict, include a fully connected layer with a size matching the number of predictors.
numHiddenUnits = 100; layers = [ ... sequenceInputLayer(numChannels, Normalization="zscore") lstmLayer(numHiddenUnits, OutputMode="last") fullyConnectedLayer(numResponses)]
layers =
3×1 Layer array with layers:
1 '' Sequence Input Sequence input with 3 dimensions
2 '' LSTM LSTM with 100 hidden units
3 '' Fully Connected 1 fully connected layer
Specify Training Options
Specify the training options. Choosing among the options requires empirical analysis. To explore different training option configurations by running experiments, you can use the Experiment Manager app.
Train using the Adam optimizer.
Train for 250 epochs. For larger data sets, you might not need to train for as many epochs for a good fit.
Specify the sequences and responses used for validation.
Output the network that gives the best, i.e. lowest, validation loss.
Set the learning rate to 0.005.
Truncate the sequences in each mini-batch to have the same length as the shortest sequence. Truncating the sequences ensures that no padding is added, at the cost of discarding data. For sequences where all of the time steps in the sequence are likely to contain important information, truncation can prevent the network from achieving a good fit.
Monitor the training progress in a plot and monitor the RMSE metric.
Disable the verbose output.
options = trainingOptions("adam", ... MaxEpochs=250, ... ValidationData={XValidation TValidation}, ... InitialLearnRate=0.005, ... SequenceLength="shortest", ... Metrics="rmse", ... Plots="training-progress", ... Verbose=false);
Train LSTM Network
Train the neural network using the trainnet function. For regression, use mean squared error loss. By default, the trainnet function uses a GPU if one is available. Using a GPU requires a Parallel Computing Toolbox™ license and a supported GPU device. For information on supported devices, see GPU Computing Requirements (Parallel Computing Toolbox). Otherwise, the function uses the CPU. To specify the execution environment, use the ExecutionEnvironment training option.
net = trainnet(XTrain,TTrain,layers,"mse",options);
Test LSTM Network
Make predictions using the minibatchpredict function. By default, the minibatchpredict function uses a GPU if one is available.
YTest = minibatchpredict(net,XTest,SequenceLength="shortest");Visualize the first few predictions in a plot.
figure tiledlayout(2,2) for i = 1:4 nexttile stackedplot(XTest{i},DisplayLabels="Channel " + (1:numChannels)) xlabel("Time Step") title("Predicted Frequency: " + string(YTest(i))) end
Visualize the mean squared errors in a histogram.
figure histogram(mean((TTest - YTest).^2,2)) xlabel("Error") ylabel("Frequency")

Calculate the overall root mean squared error.
rmse = rmse(YTest,TTest)
rmse = single
0.7605
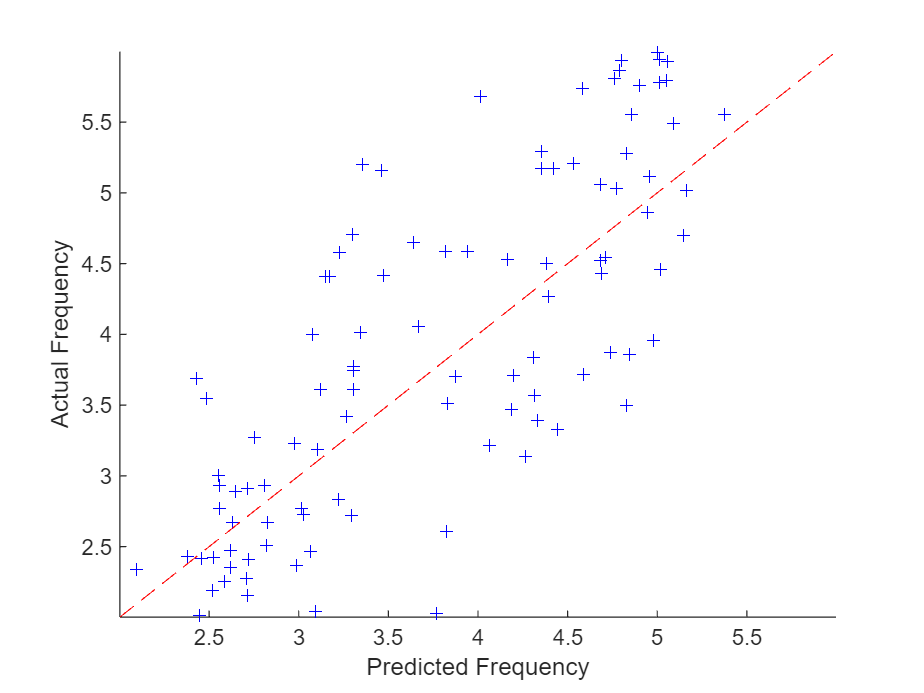
Plot the predicted frequencies against the actual frequencies.
figure scatter(YTest,TTest, "b+"); xlabel("Predicted Frequency") ylabel("Actual Frequency") hold on m = min(freq); M=max(freq); xlim([m M]) ylim([m M]) plot([m M], [m M], "r--")
See Also
trainnet | trainingOptions | dlnetwork | testnet | minibatchpredict | scores2label | predict | lstmLayer | sequenceInputLayer
See Also
Topics
- Sequence-to-Sequence Regression Using Deep Learning
- Sequence-to-Sequence Classification Using Deep Learning
- Sequence Classification Using Deep Learning
- Time Series Forecasting Using Deep Learning
- Long Short-Term Memory Neural Networks
- Deep Learning in MATLAB
- Choose Training Configurations for LSTM Using Bayesian Optimization