stcol
Scattered translates collocation matrix
Syntax
colmat = stcol(centers,x,type)
colmat = stcol(...,'tr')
Description
colmat = stcol(centers,x,type) is the
matrix whose (i,j)th entry is
with the bivariate functions ψj and the
number n depending on the centers and the
character vector or string scalar type, as detailed in the
description of stmak.
centers and x must be matrices with the same
number of rows.
The default for type is the character vector
'tp', and for this default, n equals
size(centers,2), and the functions
ψj are given by
with ψ the thin-plate spline basis function
and with |x| denoting the Euclidean norm of the vector x.
Note
See stmak for a description of
other possible values for type.
The matrix colmat is the coefficient matrix in the linear
system
that the coefficients aj of the function
f =
Σjajψj
must satisfy in order that f interpolate the value
yi at the site
x(:,i), all i.
colmat = stcol(...,'tr') returns the
transpose of the matrix returned by stcol(...).
Examples
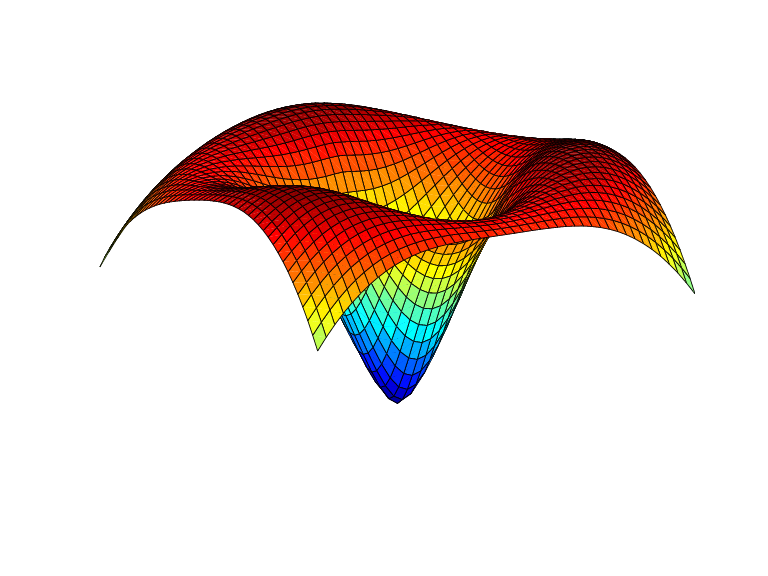
Example 1. The following evaluates and plots the function
on a regular mesh, with ψ the above thin-plate basis function, and with c1, c2, c3 three points on the unit circle; see the figure below.
a = [0,2/3*pi,4/3*pi]; centers = [cos(a), 0; sin(a), 0]; [xx,yy] = ndgrid(linspace(-2,2,45)); xy = [xx(:) yy(:)].'; coefs = [1 1 1 -3.5]; zz = reshape( coefs*stcol(centers,xy,'tr') , size(xx)); surf(xx,yy,zz), view([240,15]), axis off
Example 2. The following also evaluates, on the same mesh, and plots the length of the gradient of the function in Example 1.
zz = reshape( sqrt(...
([coefs,0]*stcol(centers,xy,'tp10','tr')).^2 + ...
([coefs,0]*stcol(centers,xy,'tr','tp01')).^2),
size(xx));
figure, surf(xx,yy,zz), view([220,-15]), axis off