fittype
Fit type for curve and surface fitting
Syntax
Description
aFittype = fittype(libraryModelName)fittype object aFittype for the model specified by libraryModelName.
aFittype = fittype(expression)
aFittype = fittype(expression,Name,Value)Name,Value pair arguments.
aFittype = fittype(linearModelTerms)linearModelTerms.
aFittype = fittype(linearModelTerms,Name,Value)Name,Value pair arguments.
aFittype = fittype(anonymousFunction)anonymousFunction.
aFittype = fittype(anonymousFunction,Name,Value)Name,Value pair arguments.
Examples
Construct fit types by specifying library model names.
Construct a fittype object for the cubic polynomial library model.
f = fittype('poly3')f =
Linear model Poly3:
f(p1,p2,p3,p4,x) = p1*x^3 + p2*x^2 + p3*x + p4
Construct a fit type for the library model rat33 (a rational model of the third degree for both the numerator and denominator).
f = fittype('rat33')f =
General model Rat33:
f(p1,p2,p3,p4,q1,q2,q3,x) = (p1*x^3 + p2*x^2 + p3*x + p4) /
(x^3 + q1*x^2 + q2*x + q3)
For a list of library model names, see libraryModelName.
Create a fit type for a custom nonlinear model, designating n as the problem-dependent parameter and u as the independent variable.
g = fittype("n*u^a",... problem="n",... independent="u")
g =
General model:
g(a,n,u) = n*u^a
Create a fit type for a logarithmic fit to some data, use the fit type to create a fit, and then plot the fit.
x = linspace(1,100); y = 7*log(x+5); myfittype = fittype("a*log(x+b)",... dependent="y",independent="x",... coefficients=["a" "b"])
myfittype =
General model:
myfittype(a,b,x) = a*log(x+b)
myfit = fit(x',y',myfittype)
Warning: Start point not provided, choosing random start point.
myfit =
General model:
myfit(x) = a*log(x+b)
Coefficients (with 95% confidence bounds):
a = 7 (7, 7)
b = 5 (5, 5)
plot(myfit,x,y)

The plot shows that the fit follows the data.
To use a linear fitting algorithm, specify a cell array of terms.
Identify the linear model terms you need to input to fittype: a*x + b*sin(x) + c. The model is linear in a, b and c. It has three terms x, sin(x) and 1 (because c=c*1). To specify this model you use this cell array of terms: LinearModelTerms = {'x','sin(x)','1'}.
Use the cell array of linear model terms as the input to fittype.
ft = fittype({'x','sin(x)','1'})ft =
Linear model:
ft(a,b,c,x) = a*x + b*sin(x) + c
Create a linear model fit type for a*cos(x) + b.
ft2 = fittype({'cos(x)','1'})ft2 =
Linear model:
ft2(a,b,x) = a*cos(x) + b
Create the fit type again and specify coefficient names.
ft3 = fittype({'cos(x)','1'},'coefficients',{'a1','a2'})ft3 =
Linear model:
ft3(a1,a2,x) = a1*cos(x) + a2
Define a function in a file and use it to create a fit type and fit a curve.
Define a function in a MATLAB® file.
type piecewiseLine.mfunction y = piecewiseLine(x,a,b,c,k)
% PIECEWISELINE A line made of two pieces
y = zeros(size(x));
% This example includes a for-loop and if statement
% purely for example purposes.
for i = 1:length(x)
if x(i) < k
y(i) = a + b.*x(i);
else
y(i) = a + b*k + c.*(x(i)-k);
end
end
end
Save the file.
Define some data and create a fit type specifying the function piecewiseLine.
x = [0.81;0.91;0.13;0.91;0.63;0.098;0.28;0.55;... 0.96;0.96;0.16;0.97;0.96]; y = [0.17;0.12;0.16;0.0035;0.37;0.082;0.34;0.56;... 0.15;-0.046;0.17;-0.091;-0.071]; ft = fittype('piecewiseLine( x, a, b, c, k )')
ft =
General model:
ft(a,b,c,k,x) = piecewiseLine( x, a, b, c, k )
The inputs to ft are the coefficients in alphabetical order, followed by the independent variables. See Input Order for Anonymous Functions to learn more.
If you want to control the order of coefficients, then use an anonymous function input. For example, to change the order of the a and b coefficients:
ft = fittype(@(b,a,c,k,x) piecewiseLine(x,a,b,c,k))
You must specify the independent variable x last.
Create a fit using the fit type ft and plot the results.
f = fit(x, y, ft, 'StartPoint', [1, 0, 1, 0.5]);
plot(f, x, y)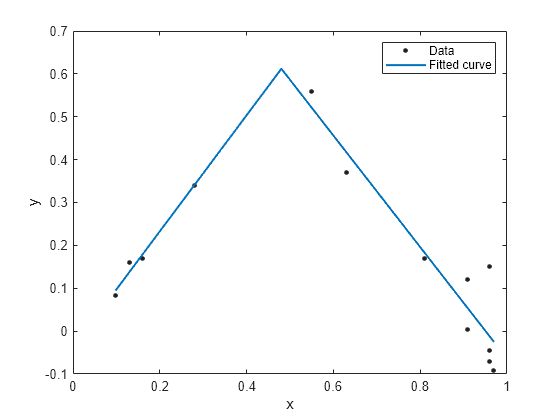
Create a fit type using an anonymous function.
g = fittype( @(a, b, c, x) a*x.^2+b*x+c )
Create a fit type using an anonymous function and specify independent and dependent parameters.
g = fittype( @(a, b, c, d, x, y) a*x.^2+b*x+c*exp(... -(y-d).^2 ), 'independent', {'x', 'y'},... 'dependent', 'z' );
Create a fit type for a surface using an anonymous function and specify independent and dependent parameters, and problem parameters that you will specify later when you call fit.
g = fittype( @(a,b,c,d,x,y) a*x.^2+b*x+c*exp( -(y-d).^2 ), ... 'problem', {'c','d'}, 'independent', {'x', 'y'}, ... 'dependent', 'z' );
Use an anonymous function to pass workspace data into the fittype and fit functions.
Create and plot an S-shaped curve. In later steps, you stretch and move this curve to fit to some data.
% Breakpoints. xs = (0:0.1:1).'; % Height of curve at breakpoints. ys = [0; 0; 0.04; 0.1; 0.2; 0.5; 0.8; 0.9; 0.96; 1; 1]; % Plot S-shaped curve. xi = linspace( 0, 1, 241 ); plot( xi, interp1( xs, ys, xi, 'pchip' ), 'LineWidth', 2 ) hold on plot( xs, ys, 'o', 'MarkerFaceColor', 'r' ) hold off title S-curve
Create a fit type using an anonymous function, taking the values from the workspace for the curve breakpoints (xs) and the height of the curve at the breakpoints (ys). Coefficients are b (base) and h (height).
ft = fittype( @(b, h, x) interp1( xs, b+h*ys, x, 'pchip' ) )Plot the fittype specifying example coefficients of base b=1.1 and height h=-0.8.
plot( xi, ft( 1.1, -0.8, xi ), 'LineWidth', 2 ) title 'Fittype with b=1.1 and h=-0.8'
Load and fit some data, using the fit type ft created using workspace values.
% Load some data xdata = [0.012;0.054;0.13;0.16;0.31;0.34;0.47;0.53;0.53;... 0.57;0.78;0.79;0.93]; ydata = [0.78;0.87;1;1.1;0.96;0.88;0.56;0.5;0.5;0.5;0.63;... 0.62;0.39]; % Fit the curve to the data f = fit( xdata, ydata, ft, 'Start', [0, 1] ) % Plot fit plot( f, xdata, ydata ) title 'Fitted S-curve'
This example shows the differences between using anonymous functions with problem parameters and workspace variable values.
Load data, create a fit type for a curve using an anonymous function with problem parameters, and call fit specifying the problem parameters.
% Load some data. xdata = [0.098;0.13;0.16;0.28;0.55;0.63;0.81;0.91;0.91;... 0.96;0.96;0.96;0.97]; ydata = [0.52;0.53;0.53;0.48;0.33;0.36;0.39;0.28;0.28;... 0.21;0.21;0.21;0.2]; % Create a fittype that has a problem parameter. g = fittype( @(a,b,c,x) a*x.^2+b*x+c, 'problem', 'c' ) % Examine coefficients. Observe c is not a coefficient. coeffnames( g ) % Examine arguments. Observe that c is an argument. argnames( g ) % Call fit and specify the value of c. f1 = fit( xdata, ydata, g, 'problem', 0, 'StartPoint', [1, 2] ) % Note: Specify start points in the calls to fit to % avoid warning messages about random start points % and to ensure repeatability of results. % Call fit again and specify a different value of c, % to get a new fit. f2 = fit( xdata, ydata, g, 'problem', 1, 'start', [1, 2] ) % Plot results. Observe the specified c constants % do not make a good fit. plot( f1, xdata, ydata ) hold on plot( f2, 'b' ) hold off
Modify the previous example to create the same fits using workspace values for variables, instead of using problem parameters. Using the same data, create a fit type for a curve using an anonymous function with a workspace value for variable c:
% Remove c from the argument list. try g = fittype( @(a,b,x) a*x.^2+b*x+c ) catch e disp( e.message ) end % Observe error because now c is undefined. % Define c and create fittype: c = 0; g1 = fittype( @(a,b,x) a*x.^2+b*x+c ) % Call fit (now no need to specify problem parameter). f1 = fit( xdata, ydata, g1, 'StartPoint', [1, 2] ) % Note that this f1 is the same as the f1 above. % To change the value of c, recreate the fittype. c = 1; g2 = fittype( @(a,b,x) a*x.^2+b*x+c ) % uses c = 1 f2 = fit( xdata, ydata, g2, 'StartPoint', [1, 2] ) % Note that this f2 is the same as the f2 above. % Plot results plot( f1, xdata, ydata ) hold on plot( f2, 'b' ) hold off
Input Arguments
Library model to fit, specified as a character vector or string scalar. This table shows some common examples.
Library Model Name | Description |
|---|---|
| Linear polynomial curve |
| Linear polynomial surface |
| Quadratic polynomial curve |
| Piecewise linear interpolation |
| Piecewise cubic interpolation |
| Smoothing spline (curve) |
| Local linear regression (surface) |
'log10' | Base-10 logarithmic curve |
'logistic4' | Four-parameter logistic curve |
For a list of library model names, see Model Names and Equations.
Example: 'poly2'
Data Types: char | string
Model to fit, specified as a character vector or string scalar. You can specify any
MATLAB command and therefore any .m file. See
Fit a Curve Defined by a File.
Data Types: char | string
Model to fit, specified as a cell array of character vectors or a string array. Specify the model terms by the expressions in the character vectors or string scalars. Do not include coefficients in the expressions for the terms. See Linear Model Terms.
Data Types: cell
Model to fit, specified as an anonymous function. For details, see Input Order for Anonymous Functions.
Data Types: char
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'coefficients',{'a1','a2'}
Coefficient names, specified as the comma-separated pair consisting of 'coefficients' and a character vector, string scalar, cell array of character vectors, or string array. You can use multicharacter symbol names. You cannot use these names: i, j, pi, inf, nan, eps.
Data Types: char | string | cell
Dependent variable name, specified as the comma-separated pair
consisting of 'dependent' and a character vector or
string scalar. If you do not specify the dependent variable, the
function assumes y is the dependent variable.
Data Types: char | string
Independent variable names, specified as the comma-separated pair
consisting of 'independent' and a character vector,
string scalar, cell array of character vectors, or string array. You can
specify a maximum of two independent variables. If you do not specify
the independent variable, the function assumes x is
the independent variable.
Data Types: char | string | cell
Fit options, specified as the comma-separated pair consisting of 'options' and the name of a fitoptions object.
Problem-dependent (fixed) parameter names, specified as the comma-separated pair consisting of 'problem' and a character vector, string scalar, cell array of character vectors, or string array with one element per problem dependent constant.
Data Types: char | string | cell
Output Arguments
Model to fit, returned as a fittype. A fittype encapsulates information describing a model. To create a fit, you need data, a fittype, and (optionally) fitoptions and an exclusion rule. You can use a fittype as an input to the fit function.
More About
How do I decide which variables are dependent and independent?
To determine dependent and independent variables and coefficients, consider this equation:
.
y is the dependent variable.
x is the independent variable.
a, b, and c are the coefficients.
The 'independent' variable is what you control. The 'dependent' variable is what you measure, i.e., it depends on the independent variable. The 'coefficients' are the parameters that the fitting algorithm estimates.
For example, if you have census data, then the year is the independent variable because it does not depend on anything. Population is the dependent variable, because its value depends on the year in which the census is taken. If a parameter like growth rate is part of the model, so the fitting algorithm estimates it, then the parameter is one of the 'coefficients'.
The fittype function determines input arguments by searching the fit type expression input for variable names. fittype assumes x is the independent variable, y is the dependent variable, and all other variables are coefficients of the model. x is used if no variable exists.
If the fit type expression input is an anonymous function, then the order of inputs must be correct. The input order enables the fittype function to determine which inputs are coefficients to estimate, problem-dependent parameters, and independent variables.
The order of the input arguments to the anonymous function must be:
fcn = @(coefficients,problemparameters,x,y) expression
y are optional. The last arguments, x and y, represent the independent variables: just x for curves, but x and y for surfaces. If you don't want to use x and/or y to name the independent variables, then specify different names using the 'independent' argument name-value pair. However, whatever name or names you choose, these arguments must be the last arguments to the anonymous function.Anonymous functions make it easier to pass other data into the fittype and fit functions.
Create a fit type using an anonymous function and a variable value (
c) from the workspace.c = 1; g = fittype( @(a, b, x) a*x.^2+b*x+c )
The
fittypefunction can use the variable values in your workspace when you create the fit type. To pass in new data from the workspace, recreate the fit type, e.g.,c = 5 % Change value of c. g = fittype( @(a, b, x) a*x.^2+b*x+c )Here, the value of
cis fixed when you create the fit type. To specify the value ofcat the time you callfit, you can use problem parameters. For example, make a fit withc = 2and then a new fit withc = 3.g = fittype( @(a,b,x,c) a*x.^2+b*x+c, 'problem', 'c' ) f1 = fit( xdata, ydata, g, 'problem', 2 ) f2 = fit( xdata, ydata, g, 'problem', 3 )
How do I define linear model terms?
To use a linear fitting algorithm, specify linearModelTerms as a cell array or string array of terms. For example:
afittype = fittype({expr1,...,exprn})expr2,...,exprn. Do not include coefficients in the expressions for the terms. If there is a constant term, use '1' as the corresponding expression in the cell array.To specify a linear model of the following form:
coeff1 * term1 + coeff2 * term2 + coeff3 * term3 + ...
term1, term2, etc., use a cell array or string array where each term, without coefficients, is specified in a cell or element of expr, as follows:LinearModelTerms = {'term1', 'term2', 'term3', ... }
For example, the model
a*x + b*sin(x) + c
a, b, and c. It has three terms x, sin(x) and 1 (because c=c*1) and therefore expr is:LinearModelTerms = {'x','sin(x)','1'}
In the Curve Fitter app, select a Linear Fitting fit in the Custom group in the Fit Type section.
Algorithms
If the fit type expression input is a character vector, string scalar, or anonymous function, then the toolbox uses a nonlinear fitting algorithm to fit the model to data.
If the fit type expression input is a cell array or string array of terms, then the toolbox uses a linear fitting algorithm to fit the model to data.
Version History
Introduced before R2006aStarting in R2024a, you can specify natural neighbor interpolant fit types for surface fits. For more information, see List of Library Models for Curve and Surface Fitting.
Starting in R2023b, you can specify sigmoidal and logarithmic fit types for curve fits. For more information, see List of Library Models for Curve and Surface Fitting.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)