Building Tunable Models

This example shows how to create tunable models of control systems for use with systune or looptune.

Background

You can tune the gains and parameters of your control system with systune or looptune. To use these commands, you need to construct a tunable model of the control system that identifies and parameterizes its tunable elements. This is done by combining numeric LTI models of the fixed elements with parametric models of the tunable elements.

Using Pre-Defined Tunable Elements

You can use one of the following "parametric" blocks to model commonly encountered tunable elements:

tunableGain: Tunable gain
tunablePID: Tunable PID controller
tunablePID2: Tunable two-degree-of-freedom PID controller
tunableTF: Tunable transfer function
tunableSS: Tunable state-space model.

For example, create a tunable model of the feedforward/feedback configuration of Figure 1 where $C$ is a tunable PID controller and $F$ is a tunable first-order transfer function.

Figure 1: Control System with Feedforward and Feedback Paths

First model each block in the block diagram, using suitable parametric blocks for $C$ and $F$ .

G = tf(1,[1 1]); 
C = tunablePID('C','pid');  % tunable PID block
F = tunableTF('F',0,1);     % tunable first-order transfer function

Then use connect to build a model of the overall block diagram. To specify how the blocks are connected, label the inputs and outputs of each block and model the summing junctions using sumblk.

G.u = 'u';  G.y = 'y';
C.u = 'e';  C.y = 'uC';
F.u = 'r';  F.y = 'uF';

% Summing junctions
S1 = sumblk('e = r-y');
S2 = sumblk('u = uF + uC');

T = connect(G,C,F,S1,S2,'r','y')

Generalized continuous-time state-space model with 1 outputs, 1 inputs, 3 states, and the following blocks:
  C: Tunable PID controller, 1 occurrences.
  F: Tunable SISO transfer function, 0 zeros, 1 poles, 1 occurrences.

Type "ss(T)" to see the current value and "T.Blocks" to interact with the blocks.

This creates a generalized state-space model T of the closed-loop transfer function from r to y. This model depends on the tunable blocks C and F. You can use systune to automatically tune the PID gains and the feedforward coefficients a,b subject to your performance requirements. Use showTunable to see the current value of the tunable blocks.

showTunable(T)

C =
 
        1 
  Ki * ---
        s 

  with Ki = 0.001
 
Name: C
Continuous-time I-only controller.
-----------------------------------
F =
 
    10
  ------
  s + 10
 
Name: F
Continuous-time transfer function.

Interacting with the Tunable Parameters

You can adjust the parameterization of the tunable elements $C$ and $F$ by interacting with the objects C and F. Use get to see their list of properties.

get(C)

             Kp: [1x1 param.Continuous]
             Ki: [1x1 param.Continuous]
             Kd: [1x1 param.Continuous]
             Tf: [1x1 param.Continuous]
       IFormula: ''
       DFormula: ''
      InputName: {'e'}
      InputUnit: {''}
     InputGroup: [1x1 struct]
     OutputName: {'uC'}
     OutputUnit: {''}
    OutputGroup: [1x1 struct]
          Notes: [0x1 string]
       UserData: []
           Name: 'C'
             Ts: 0
       TimeUnit: 'seconds'

A PID controller has four tunable parameters Kp,Ki,Kd,Tf. The tunable block C contains a description of each of these parameters. Parameter attributes include current value, minimum and maximum values, and whether the parameter is free or fixed.

C.Kp

 
ans =
 
       Name: 'Kp'
      Value: 0
    Minimum: -Inf
    Maximum: Inf
       Free: 1
      Scale: 1
       Info: [1x1 struct]

 
1x1 param.Continuous

Set the corresponding attributes to override defaults. For example, you can fix the time constant Tf to the value 0.1 by

C.Tf.Value = 0.1;
C.Tf.Free = false;

Creating Custom Tunable Elements

For tunable elements not covered by the pre-defined blocks listed above, you can create your own parameterization in terms of elementary real parameters (realp). Consider the low-pass filter

$F (s) = \frac{a}{s + a}$

where the coefficient $a$ is tunable. To model this tunable element, create a real parameter $a$ and define $F$ as a transfer function whose numerator and denominator are functions of $a$ . This creates a generalized state-space model F of the low-pass filter parameterized by the tunable scalar a.

a = realp('a',1);   % real tunable parameter, initial value 1
F = tf(a,[1 a])

Generalized continuous-time state-space model with 1 outputs, 1 inputs, 1 states, and the following blocks:
  a: Scalar parameter, 2 occurrences.

Type "ss(F)" to see the current value and "F.Blocks" to interact with the blocks.

Similarly, you can use real parameters to model the notch filter

$N (s) = \frac{s^{2} + 2 ζ_{1} ω_{n} s + ω_{n}^{2}}{s^{2} + 2 ζ_{2} ω_{n} s + ω_{n}^{2}}$

with tunable coefficients $ω_{n}, ζ_{1}, ζ_{2}$ .

wn = realp('wn',100);
zeta1 = realp('zeta1',1);   zeta1.Maximum = 1;    % zeta1 <= 1
zeta2 = realp('zeta2',1);   zeta2.Maximum = 1;    % zeta2 <= 1
N = tf([1 2*zeta1*wn wn^2],[1 2*zeta2*wn wn^2]);  % tunable notch filter

You can also create tunable elements with matrix-valued parameters. For example, model the observer-based controller $C (s)$ with equations

$\frac{d x}{d t} = A x + B u + L (y - C x), u = - K x$

and tunable gain matrices $K$ and $L$ .

% Plant with 6 states, 2 controls, 3 measurements
[A,B,C] = ssdata(rss(6,3,2));

K = realp('K',zeros(2,6));
L = realp('L',zeros(6,3));

C = ss(A-B*K-L*C,L,-K,0)

Generalized continuous-time state-space model with 2 outputs, 3 inputs, 6 states, and the following blocks:
  K: Tunable 2x6 matrix, 2 occurrences.
  L: Tunable 6x3 matrix, 2 occurrences.

Type "ss(C)" to see the current value and "C.Blocks" to interact with the blocks.

Enabling Open-Loop Requirements

The systune command takes a closed-loop model of the overall control system, like the tunable model T built at the beginning of this example. Such models do not readily support open-loop analysis or open-loop specifications such as loop shapes and stability margins. To gain access to open-loop responses, insert an AnalysisPoint block as shown in Figure 2.

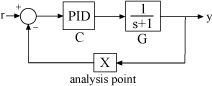
Figure 2: Analysis Point Block

The AnalysisPoint block can be used to mark internal signals of interest as well as locations where to open feedback loops and measure open-loop responses. This block evaluates to a unit gain and has no impact on the model responses. For example, construct a closed-loop model T of the feedback loop of Figure 2 where $C$ is a tunable PID.

G = tf(1,[1 1]);
C = tunablePID('C','pid');
AP = AnalysisPoint('X');
T = feedback(G*C,AP);

You can now use getLoopTransfer to compute the (negative-feedback) loop transfer function measured at the location "X". Note that this loop transfer function is $L = G C$ for the feedback loop of Figure 2.

L = getLoopTransfer(T,'X',-1);  % loop transfer at "X"
clf, bode(L,'b',G*C,'r--')

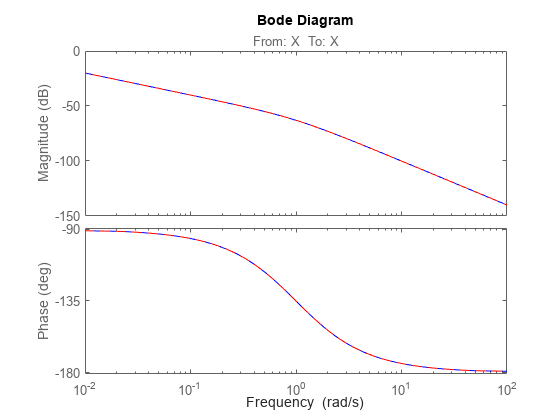
MATLAB figure

You can also refer to the location "X" when specifying target loop shapes or stability margins for systune. The requirement then applies to the loop transfer measured at this location.

% Target loop shape for loop transfer at "X"
Req1 = TuningGoal.LoopShape('X',tf(5,[1 0]));

% Target stability margins for loop transfer at "X"
Req2 = TuningGoal.Margins('X',6,40);

In general, loop opening locations are specified in the Location property of AnalysisPoint blocks. For single-channel analysis points, the block name is used as default location name. For multi-channel analysis points, indices are appended to the block name to form the default location names.

AP = AnalysisPoint('Y',2);  % two-channel analysis point
AP.Location

ans = 2x1 cell
    {'Y(1)'}
    {'Y(2)'}

You can override the default location names and use more descriptive names by modifying the Location property.

% Rename loop opening locations to "InnerLoop" and "OuterLoop".
AP.Location = {'InnerLoop' ; 'OuterLoop'};
AP.Location

ans = 2x1 cell
    {'InnerLoop'}
    {'OuterLoop'}