getSensitivity
Sensitivity function from generalized model of control system
Description
S = getSensitivity(T,location)
S = getSensitivity(T,location,opening)
If opening and location list the same
point, the software opens the loop after measuring the signal at the
point.
Examples
Sensitivity Function at a Location
Compute the sensitivity at the plant input, marked by the analysis point X.
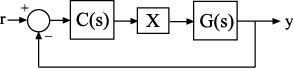
Create a model of the system by specifying and connecting a numeric LTI plant model G, a tunable controller C, and the AnalysisPoint block X. Use the AnalysisPoint block to mark the location where you assess the sensitivity (plant input in this example).
G = tf([1],[1 5]); C = tunablePID('C','p'); C.Kp.Value = 3; X = AnalysisPoint('X'); T = feedback(G*X*C,1);
T is a genss model that represents the closed-loop response of the control system from to . The model contains the AnalysisPoint block, X, that identifies the analysis point.
Calculate the sensitivity, , at X.
S = getSensitivity(T,'X');
tf(S)ans = From input "X" to output "X": s + 5 ----- s + 8 Continuous-time transfer function.
Specify Additional Loop Opening for Sensitivity Function Calculation
Calculate the inner-loop sensitivity at the output of G2, with the outer loop open.
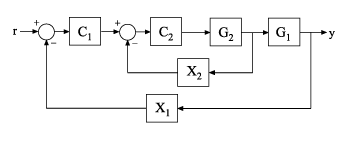
Create a model of the system by specifying and connecting the numeric plant models, tunable controllers, and AnalysisPoint blocks. G1 and G2 are plant models, C1 and C2 are tunable controllers, and X1 and X2 are AnalysisPoint blocks that mark potential loop-opening locations.
G1 = tf(10,[1 10]); G2 = tf([1 2],[1 0.2 10]); C1 = tunablePID('C','pi'); C2 = tunableGain('G',1); X1 = AnalysisPoint('X1'); X2 = AnalysisPoint('X2'); T = feedback(G1*feedback(G2*C2,X2)*C1,X1);
Calculate the sensitivity, , at X2, with the outer loop open at X1.
S = getSensitivity(T,'X2','X1'); tf(S)
ans = From input "X2" to output "X2": s^2 + 0.2 s + 10 ---------------- s^2 + 1.2 s + 12 Continuous-time transfer function.
Input Arguments
T — Model of control system
generalized state-space model
Model of a control system, specified as a generalized state-space model
(genss).
Locations at which you can perform sensitivity analysis or open loops are
marked by AnalysisPoint blocks in
T. Use getPoints(T) to get the
list of such locations.
location — Location
character vector | cell array of character vectors
Location at which you calculate the sensitivity function, specified as a character vector or cell array of character vectors. To extract the sensitivity function at multiple locations, use a cell array of character vectors.
Each specified location must match an analysis point in
T. Analysis points are marked using
AnalysisPoint blocks. To get the list of available
analysis points in T, use
getPoints(T).
Example: 'u' or
{'u','y'}
opening — Additional loop opening
character vector | cell array of character vectors
Additional loop opening used to calculate the sensitivity function, specified as a character vector or cell array of character vectors. To open the loop at multiple locations, use a cell array of character vectors.
Each specified opening must match an analysis point in
T. Analysis points are marked using
AnalysisPoint blocks. To get the list of available
analysis points in T, use
getPoints(T).
Use an opening, for example, to calculate the sensitivity function of an inner loop, with the outer loop open.
If opening and location list the
same point, the software opens the loop after measuring the signal at the
point.
Example: 'y_outer' or
{'y_outer','y_outer2'}
Output Arguments
S — Sensitivity function
generalized state-space model
Sensitivity
function of the control system, T, measured
at location, returned as a generalized state-space
model (genss).
If
locationspecifies a single analysis point, thenSis a SISOgenssmodel.If
locationis a vector signal, or specifies multiple analysis points, thenSis a MIMOgenssmodel.
More About
Sensitivity Function
The sensitivity function, also referred to
simply as sensitivity, measures how sensitive a signal is to
an added disturbance. Feedback reduces the sensitivity in the frequency band where
the open-loop gain is greater than 1.
Consider the following model:
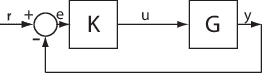
The sensitivity, Su, at
u is defined as the transfer function from
du to u:

Here, I is an identity matrix of the same size as KG.
Sensitivity at multiple locations, for example, u and
y, is defined as the MIMO transfer function from the
disturbances to sensitivity measurements:

Version History
Introduced in R2014a
See Also
getPoints | AnalysisPoint | genss | getLoopTransfer | systune | getIOTransfer | getCompSensitivity | getValue | getSensitivity (Simulink Control Design)
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)