Main Content

Correct Misalignment of Symbol Boundaries

Open Model

Nonlinear digital demodulation techniques can be more prone to issues caused by misalignment of symbol boundaries due to their sensitivity to timing errors, increased susceptibility to intersymbol interference (ISI), and potential for introducing nonlinear distortions. For the demodulation to work correctly, the input signal to the demodulator block must have the correct alignment. Various blocks between the modulator and the demodulator introduce processing delays, leading to incorrect alignment. This example shows how to correct this type of misalignment.

Open the Model

The model includes the following blocks:

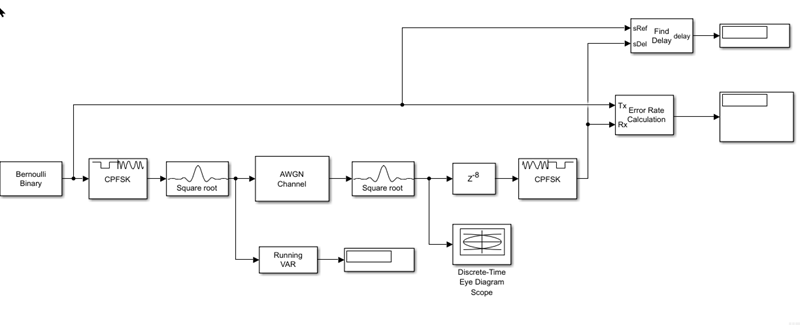
Adjust Delays

The CPFSK Demodulator block processes each collection of eight samples per symbol to compute one output symbol. For binary CPFSK with a modulation index of 1/2, the demodulator input must align along even numbers of symbols. The requirement applies only to binary CPFSK with a modulation index of 1/2. Other CPM schemes with different M-ary values and modulation indexes have different requirements.

Both the Raised Cosine Transmit Filter and the Raised Cosine Receive Filter introduces a group delay (GD) in the system. Set the Filter Span in Symbols property in both the filters to 2*2 . GD in symbols is half of the filter span which is 2 , and the combined GD is 4.

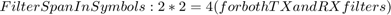
$$FilterSpanInSymbols: 2 * 2 = 4 (for both TX and RX filters)$$

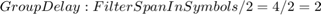
$$Group Delay: FilterSpanInSymbols/2 = 4/2 = 2$$

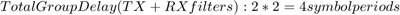
$$Total Group Delay (TX + RX filters): 2 * 2 = 4 symbol periods$$

To ensure that the CPFSK Demodulator block receives the input samples in aligned to the start of the traceback depth specified in the block, you use the Delay block to introduce a delay of 12 samples. In sample-based mode, the CPFSK Demodulator block introduces a delay of Traceback length + 1 samples at its output. With a Traceback length of 16, the total CPFSK Demodulator Delay is 17 andthe total receiver delay is 17 + 2 = 19 samples.

Run the Model

When you run the model, you can see:

Evaluate Error Rates

The Error Rate Calculation block shows a minimal error count, indicating an overall low error rate in the system compared to the number of samples evaluated. This outcome results from the the absence of alignment issues, ensuring high data integrity and system performance.

To establish a baseline, remove the noise from the system by deleting the AWGN Channel block from the model. The Error Rate Calculation block then reports zero errors.

Observe Effects of Misalignment

In the model, remove the delay block. The demodulator input does not align along even numbers of symbols. Consequently, this misalignment leads to a significant increase in the error rate and the number of errors reported by the Error Rate Calculation block.

Conclusion

Managing delays and alignment ensures data integrity and system performance. By incorporating a delay block to compensate for the misalignment caused by the Raised Cosine Transmit and Receive Filter blocks, you can see that the model successfully aligns the symbol boundaries before the demodulation process and reduces the overall error rates.

Related Topics