OSTBC Combiner
Combine inputs using orthogonal space-time block code
Libraries:
Communications Toolbox /
MIMO
Description
The OSTBC Combiner block combines the input signal (from all of the receive antennas) and the channel estimate signal to extract the soft information of the symbols encoded by an orthogonal space-time block code (OSTBC). The input channel estimate does not need to be constant and can vary each time you run the block. The combining algorithm uses only the estimate for the first symbol period per codeword block. A multiple-input multiple-output (MIMO) communications system applies symbol demodulation or decoding after the OSTBC combining process.
The block conducts the combining operation for each symbol independently. The combining algorithm depends on the structure of the OSTBC. For more information, see OSTBC Combining Algorithm.
Examples
Simulate orthogonal space-time block codes (OSTBC) to achieve diversity gains in a multiple-input multiple-output (MIMO) communications system. The example shows the transmission of data over three transmit antennas and two receive antennas using independent Rayleigh fading per link.
Explore Model
The doc_ostc32 model creates a random binary signal, modulates it using a binary phase shift keying (BPSK) technique, and then encodes the waveform using a rate 3/4 orthogonal space-time block code for transmission over the fading channel. The fading channel has six independent links that result from the configuration of single-path Rayleigh fading processes. The simulation adds white Gaussian noise at the receiver, and then combines the signals from both receive antennas into a single stream for demodulation. For this combining process, the model assumes perfect knowledge of the channel gains at the receiver. The simulation compares the demodulated data with the original transmitted data and computes the bit error rate. The simulation runs until it processes 100 errors or 1e6 bits, whichever comes first.
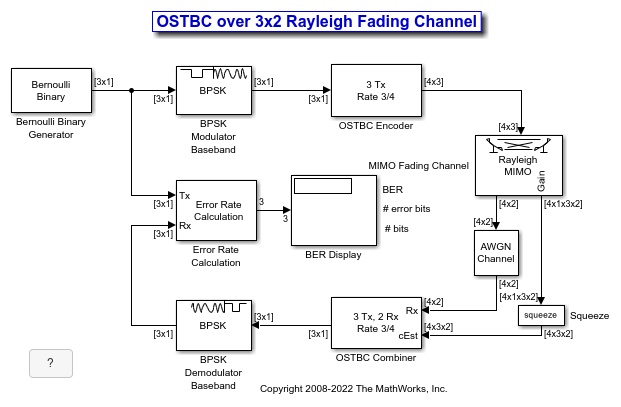
Orthogonal Space-Time Block Code
This matrix shows the rate 3/4 code with three transmit antenna orthogonal space-time block code configured in the OSTBC Encoder block:

where 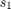 ,
, 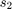 , and
, and  correspond to the three symbol inputs for which the output is given by the matrix. The input to the OSTBC Encoder block is a 3-by-1 vector signal and the output is a 4-by-3 matrix. The number of columns in the output signal indicates the number of transmit antennas for this simulation, where the first dimension is for time. The OSTBC Combiner block outputs a 3-by-1 vector.
correspond to the three symbol inputs for which the output is given by the matrix. The input to the OSTBC Encoder block is a 3-by-1 vector signal and the output is a 4-by-3 matrix. The number of columns in the output signal indicates the number of transmit antennas for this simulation, where the first dimension is for time. The OSTBC Combiner block outputs a 3-by-1 vector.
For the rate 3/4 OSTBC code modeled, the output signal power per time step is 3x(3/4) = 2.25W. A channel symbol carries 3 data bits, is 4 time steps long, and has a period of 3e-3 seconds. At the receiver, two antennas result in 3/2 bits per symbol per channel (antenna). In addition,
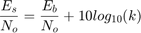
where k is the number of bits per symbol. Since the AWGN Channel block requires per-channel values for input signal power and number of bits per symbol, set the Es/No value to EbNo+10*log10(3/2) to calibrate the white Gaussian noise added in the simulation.
Performance
Compare the performance of the model to theoretical results by using the Bit Error Rate Analysis app. This plot compares the simulated BER for a range of Eb/No values with the theoretical results for a diversity order of six.

The theoretical and simulated results align well. The variation between theoretical and simulated results is primarily due to the simulated fading channel model having a small Doppler fade. Since the simulated channel varies slightly over the block symbols, the simulated and theoretical results show some variation.
Ports
Input
Received signal, specified as a matrix or 3-D array. For more information, see Input-to-Output Dimensions.
Data Types: single | double | fixed point
Complex Number Support: Yes
Channel estimate, specified as a matrix or 3-D array. For more information, see Input-to-Output Dimensions.
Data Types: single | double | fixed point
Complex Number Support: Yes
Output
Output data, returned as a matrix or 3-D array. For more information, see Input-to-Output Dimensions.
The output signal inherits the data type from the input signal. For fixed-point signals, the complex conjugation might cause overflows, which you must manage with the Saturate on integer overflow fixed-point parameter.
This port is unnamed on the block icon.
Data Types: single | double | fixed point
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
Main
Number of transmit antennas, specified as 2,
3, or 4.
Symbol rate of the code, specified as 3/4 or
1/2. When you set Number of
transmit antennas to 2, the symbol rate
is 1.
Dependencies
To enable this parameter, set Number of transmit
antennas to 3 or
4.
Number of receive antennas, specified as an integer in the range [1,8].
Data Types
Rounding mode for fixed-point calculations, specified as
Floor, Ceiling,
Convergent,
Nearest, Round,
Simplest, or Zero.
The block uses rounding method specified by this parameter to round off the
calculation to a representable number if a value cannot be represented
exactly by the specified data type and scaling. For more information, see
Rounding (Fixed-Point Designer).
For fixed-point calculations, use this parameter to specify the method to be used if the magnitude of a fixed-point calculation result does not fit into the range of the data type and scaling that stores the result.
To saturate on integer overflow, select this parameter.
To wrap on integer overflow, do not select this parameter.
For more information, see Precision and Range.
Data Types: Boolean
Complex product in the numerator for diversity combining, specified as
Inherit: Inherit via internal rule,
Inherit: Same as product output,
fixdt(1,16,0), or a custom
<data type expression>. For more
information, see Fixed-Point Signals.
Summation in the numerator for diversity combining. Fixed-point blocks that must hold summation results for further calculation usually allow you to specify the data type and scaling of the accumulator. Most such blocks cast to the accumulator data type before summation:

Use the Accumulator >> Mode parameter to specify how you would like to designate the accumulator word and fraction lengths:
When you select
Inherit via internal rule, the accumulator output word and fraction lengths are automatically calculated for you. For more information, see Inherit via Internal Rule.When you select
Same as product output, these characteristics match those of the product output.When you select
Same as input, these characteristics match those of the first input to the block.When you select
Binary point scaling, you are able to enter the word length and the fraction length of the accumulator, in bits.When you select
Slope and bias scaling, you are able to enter the word length, in bits, and the slope of the accumulator. The bias of all signals in DSP System Toolbox™ software is zero.
Complex product in the denominator for calculating total energy in the
MIMO channel, specified as Inherit: Inherit via internal
rule, Inherit: Same as product
output, fixdt(1,16,0), or a
custom <data type expression>.
Summation in the denominator for calculating total energy in the MIMO
channel, specified as Inherit: Inherit via internal
rule, Inherit: Same as
accumulator, Inherit: Same as energy product
output, fixdt(1,16,0), or a
custom <data type expression>
Normalized diversity combining by total energy in the MIMO channel,
specified as Inherit: Same as accumulator,
fixdt(1,16,0), or a custom
<data type expression>.
Block Characteristics
More About
The OSTBC combiner supports time and spatial domains for OSTBC transmission and an optional dimension over which the combining calculation is independent. This illustration indicates the supported input dimensions and resulting output dimensions.
This table shows the supported input and output dimensions, which depend upon the values of F and M.
| Values of F and M | Rx Input | cEst Input | Output |
|---|---|---|---|
| F = 1 and M = 1 | Column vector | 2-D | Column vector |
| F = 1 and M > 1 | 2-D | 3-D | Column vector |
| F > 1 and M = 1 | 2-D | 3-D | 2-D |
| F > 1 and M > 1 | 3-D | 4-D | 2-D |
R — Symbol rate of the code, as specified by the Rate parameter.
For N = 2, R must be 1.
For N = 3 or 4, R can be 3/4 or 1/2.
N — Number of transmit antennas must be 2, 3, or 4, and is specified by the Number of transmit antennas parameter.
M — Number of receive antennas must be an integer in the range [1,8], and is specified by the Number of receive antennas parameter.
T/R — Input symbol sequence length for the time domain. The time domain length T/R must be a multiple of the number of symbols in each codeword matrix.
For N = 2 or R = 1/2, T/R must be a multiple of 2.
For R = 3/4, T/R must be a multiple of 3.
T — Symbol sequence length in time domain for the output signal.
For N = 2, T is a multiple of 2.
For N = 3 or 4, T is a multiple of 4.
F — Additional dimension; typically the frequency domain. The combining calculation is independent of this dimension. F can be any positive integer.
To highlight the data types used for fixed-point signals, use this equation for for Alamouti code with one receive antenna:
In this equation, the data types for the Product output and Accumulator parameters correspond to the product and summation in the numerator. Similarly, the types for the Energy product output and Energy accumulator parameters correspond to the product and summation in the denominator.
Signal Flow Diagram for s1 Combining Calculation of Alamouti Code with One Receive Antenna

This equation shows the data types that the OSTBC combiner uses for fixed-point signals in the Alamouti code when the number of receive antennas, M, is greater than one.
Signal Flow Diagram for Complex Multiply of a + ib and c + id

For binary point scaling, you cannot specify WLp and FLp. Instead, the block determines these values implicitly from WLa and FLa.
The internal rule for the Product output and Energy product output parameters are:
When you select
Inherit via internal rule, the internal rule determines WLp and FLp. Therefore, WLa = WLp + 1 and FLa = FLpFor
Binary point scaling, you specify WLa and FLa. Therefore, WLp = WLa – 1 and FLa = FLp.
For information on how the internal rule applies to the Accumulator and Energy Accumulator parameters, see Inherit via Internal Rule.
Algorithms
The OSTBC combiner algorithm implements the five different OSTBC combining computation matrices shown in this table. The number of transmit antennas and the symbol rate determine the codeword matrix that the algorithm uses to combine the received signal.
| Number of Transmit Antennas | Rate | Computational Algorithm per Codeword Block Length |
|---|---|---|
| 2 | 1 |
|
| 3 | 1/2 |
|
| 3 | 3/4 |
|
| 4 | 1/2 |
|
| 4 | 3/4 |
|
represents the estimated kth symbol in the OSTBC codeword matrix.
hij represents the estimate for the channel from the ith transmit antenna and the jth receive antenna.
Values for i must be in the range [1,N], where N is the number of transmit antennas.
Values for j must be in the range [1,M], where M is the number of receive antennas.
rlj represents the lth symbol at the jth receive antenna per codeword block.
Values for l must be in the range [1,L], where L is the codeword block length.
represents the summation of channel power per link. Specifically,
Values for l must be in the range [1,L], where L is the codeword block length.
represents the summation of channel power per link. Specifically,
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2009a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)