mdct
Modified discrete cosine transform
Description
Y = mdct(X,win,Name,Value)Name to the specified Value.
Unspecified properties have default values.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
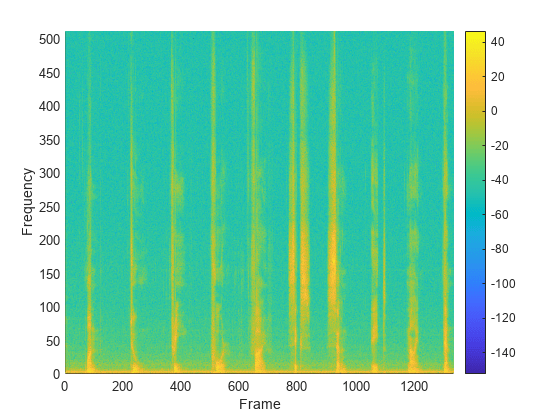
The modified discrete cosine transform is a time-frequency transform. Given an input
signal X and window win, the
mdct function performs the following steps for each independent channel:
The frame size is the number of elements in the specified window, N =
numel(. By default,win)PadInputis set totrue, so the input signalXis padded with N/2 zeros on the front and back. If the input signal is not divisible by N, additional padding is added on the back. After padding, the input signal is buffered into 50% overlapped frames.Each frame of the buffered and padded input signal is multiplied by the window,
win.The input is converted into a frequency representation using the modified discrete cosine transform:
To take advantage of the FFT algorithm, the MDCT is calculated by first calculating the odd DFT:
and then calculating the MDCT:
If a second argument is requested from the mdct
function, the modified discrete sine transform (MDST) is also computed and returned:
References
[1] Princen, J., A. Johnson, and A. Bradley. "Subband/Transform Coding Using Filter Bank Designs Based on Time Domain Aliasing Cancellation." IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP). 1987, pp. 2161–2164.
[2] Princen, J., and A. Bradley. "Analysis/Synthesis Filter Bank Design Based on Time Domain Aliasing Cancellation." IEEE Transactions on Acoustics, Speech, and Signal Processing. Vol. 34, Issue 5, 1986, pp. 1153–1161.
Extended Capabilities
Version History
Introduced in R2019a