acousticSharpness
Perceived sharpness of acoustic signal
Syntax
Description
sharpness = acousticSharpness(audioIn,fs,calibrationFactor)
sharpness = acousticSharpness(specificLoudnessIn)
sharpness = acousticSharpness(___,Name,Value)Name,Value pair arguments.
Example: sharpness =
acousticSharpness(audioIn,fs,calibrationFactor,'SoundField','diffuse') returns
sharpness assuming a diffuse sound field.
acousticSharpness(___,
with no output arguments plots sharpness relative to time.TimeVarying,true)
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
Acoustic sharpness is a measurement derived from acoustic loudness. The acoustic loudness
algorithm is described in [1] and implemented in the
acousticLoudness
function. The acoustic sharpness calculation is described in [2]. The algorithm for acoustic
sharpness is outlined as follows.
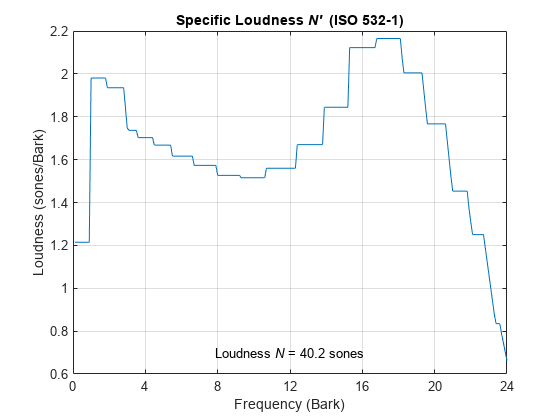
Where N' is the specific loudness in sones/Bark. The
function g(z) and the scaling factor
k depend on the specified Weighting method:
'DIN 45692': k is
set such that a 1 kHz reference tone results in a 1 acum sharpness measurement, and
'von Bismark': k is
set to 0.11, and
'Aures': k is set
to 0.11, and
References
[1] ISO 532-1:2017(E). "Acoustics – Methods for calculating loudness – Part 1: Zwicker method." International Organization for Standardization.
[2] DIN 45692:2009. "Measurement Technique for the Simulation of the Auditory Sensation of Sharpness." German Institute for Standardization.
Extended Capabilities
Version History
Introduced in R2020a