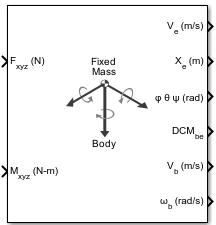
6DOF (Euler Angles)
Implement Euler angle representation of six-degrees-of-freedom equations of motion
Libraries:
Aerospace Blockset /
Equations of Motion /
6DOF
Alternative Configurations of 6DOF (Euler Angles) Block:
Simple Variable Mass 6DOF (Euler Angles) | Custom Variable Mass 6DOF (Euler Angles)
Description
The 6DOF (Euler Angles) block implements the Euler angle representation of six-degrees-of-freedom equations of motion, taking into consideration the rotation of a body-fixed coordinate frame (Xb, Yb, Zb) about a flat Earth reference frame (Xe, Ye, Ze). For more information about these reference points, see Algorithms.
The 6DOF (Euler Angles), Simple Variable Mass 6DOF (Euler Angles), and Custom Variable Mass 6DOF (Euler Angles) blocks are alternative configurations of the same block.
6DOF (Euler Angles) — Implement Euler angle representation of six-degrees-of-freedom equations of motion
Simple Variable Mass 6DOF (Euler Angles) — Implement Euler angle representation of six-degrees-of-freedom equations of motion of simple variable mass
Custom Variable Mass 6DOF (Euler Angles) — Implement Euler angle representation of six-degrees-of-freedom equations of motion of custom variable mass
Limitations
The block assumes that the applied forces act at the center of gravity of the body, and that the mass and inertia are constant.
Ports
Input
Output
Parameters
Alternative Configurations
Algorithms
The 6DOF (Euler Angles) block uses these reference frame concepts.
The origin of the body-fixed coordinate frame is the center of gravity of the body, and the body is assumed to be rigid, an assumption that eliminates the need to consider the forces acting between individual elements of mass.
The flat Earth reference frame is considered inertial, an excellent approximation that allows the forces due to the Earth motion relative to the "fixed stars" to be neglected.

Translational motion of the body-fixed coordinate frame, where the applied forces [Fx Fy Fz]T are in the body-fixed frame, and the mass of the body m is assumed constant.
The rotational dynamics of the body-fixed frame, where the applied moments are [L M N]T, and the inertia tensor I is with respect to the origin O.
The relationship between the body-fixed angular velocity vector, [p q r]T, and the rate of change of the Euler angles, , are determined by resolving the Euler rates into the body-fixed coordinate frame.
Inverting J then gives the required relationship to determine the Euler rate vector.
References
[1] Stevens, Brian, and Frank Lewis, Aircraft Control and Simulation. Hoboken, NJ: Second Edition, John Wiley & Sons, 2003.
[2] Zipfel, Peter H., Modeling and Simulation of Aerospace Vehicle Dynamics. Reston, Va: Second Edition, AIAA Education Series, 2007.
Extended Capabilities
Version History
Introduced in R2006aSee Also
6DOF (Quaternion) | 6DOF ECEF (Quaternion) | 6DOF Wind (Quaternion) | 6DOF Wind (Wind Angles) | Custom Variable Mass 6DOF (Euler Angles) | Custom Variable Mass 6DOF (Quaternion) | Custom Variable Mass 6DOF ECEF (Quaternion) | Custom Variable Mass 6DOF Wind (Quaternion) | Custom Variable Mass 6DOF Wind (Wind Angles) | Simple Variable Mass 6DOF (Euler Angles) | Simple Variable Mass 6DOF (Quaternion) | Simple Variable Mass 6DOF ECEF (Quaternion) | Simple Variable Mass 6DOF Wind (Quaternion) | Simple Variable Mass 6DOF Wind (Wind Angles)