Matrix Indexing in MATLAB

Indexing into a matrix is a means of selecting or modifying a subset of elements from the matrix. MATLAB^® has several indexing styles that are not only powerful and flexible, but also readable and expressive. Matrices are a core component of MATLAB for organizing and analyzing data, and indexing is key to the effectiveness of manipulating matrices in an understandable way.

Indexing is closely related to another term MATLAB users often hear: vectorization. Vectorization means using MATLAB matrix and vector operations instead of scalar operations—usually resulting in code that is shorter, more mathematically expressive and readable, and sometimes faster.

Indexing Vectors

Let’s start with the simple case of a vector and subscripts.

  v = [16 5 9 4 2 11 7 14];

The subscript can be a single value:

  v(3)     % Extract the third element
  ans =
      9

Or a subscript can itself be another vector.

  v([1 5 6])      % Extract the first, fifth, and sixth elements
  ans =
      16   2   11

The colon notation in MATLAB provides an easy way to extract a range of elements from v.

  v(3:7)     % Extract the third through the seventh elements
  ans =
      9   4   2   11   7

Swap the two halves of v to make a new vector.

  v2 = v([5:8 1:4])     % Extract and swap the halves of v
  v2 =
     2   11   7   14   16   5   9   4

The special end operator is an easy shorthand way to refer to the last element of v.

  v(end)     % Extract the last element
  ans =
      14

The end operator can be used in a range.

  v(5:end)     % Extract the fifth through the last elements
  ans =
      2   11   7   14

You can even do arithmetic using end.

  v(2:end-1)     % Extract the second through the next-to-last elements
  ans =
      5   9   4   2   11   7

Combine the colon operator and end to achieve a variety of effects, such as extracting every k-th element or flipping the entire vector.

  v(1:2:end)   % Extract all the odd elements
  ans =
      16   9   2   7
  v(end:-1:1)   % Reverse the order of elements
  ans =
      14   7   11   2   4   9   5   16

By using an indexing expression on the left side of the equal sign, you can replace certain elements of the vector.

  v([2 3 4]) = [10 15 20]   % Replace some elements of v
  v =
    16   10   15   20   2   11   7   14

Usually, the number of elements on the right must be the same as the number of elements referred to by the indexing expression on the left. You can always, however, use a scalar on the right side. This is called scalar expansion.

  v([2 3]) = 30   % Replace second and third elements by 30
  v =
    16   30   30   20   2   11   7   14

Indexing Matrices with Two Subscripts

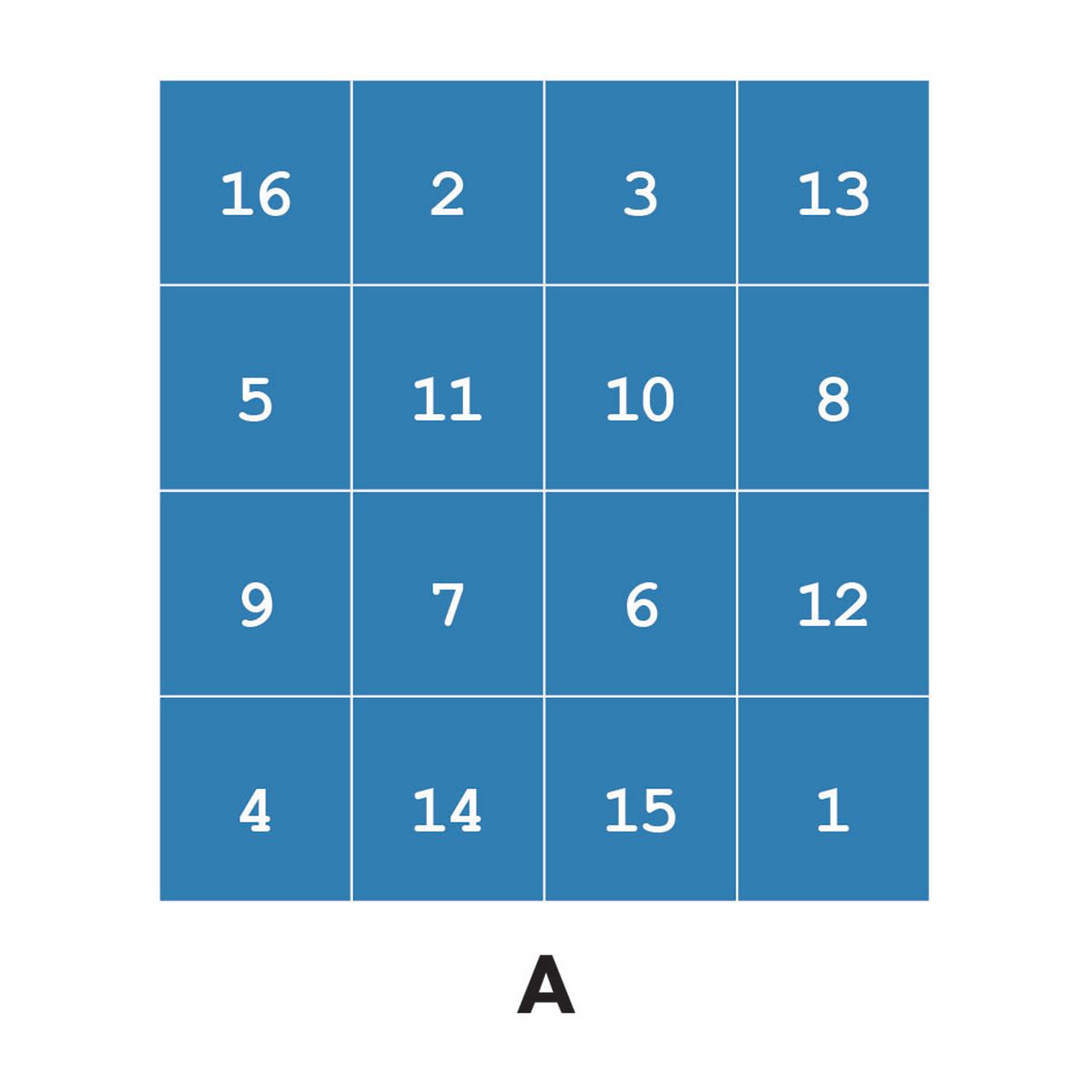
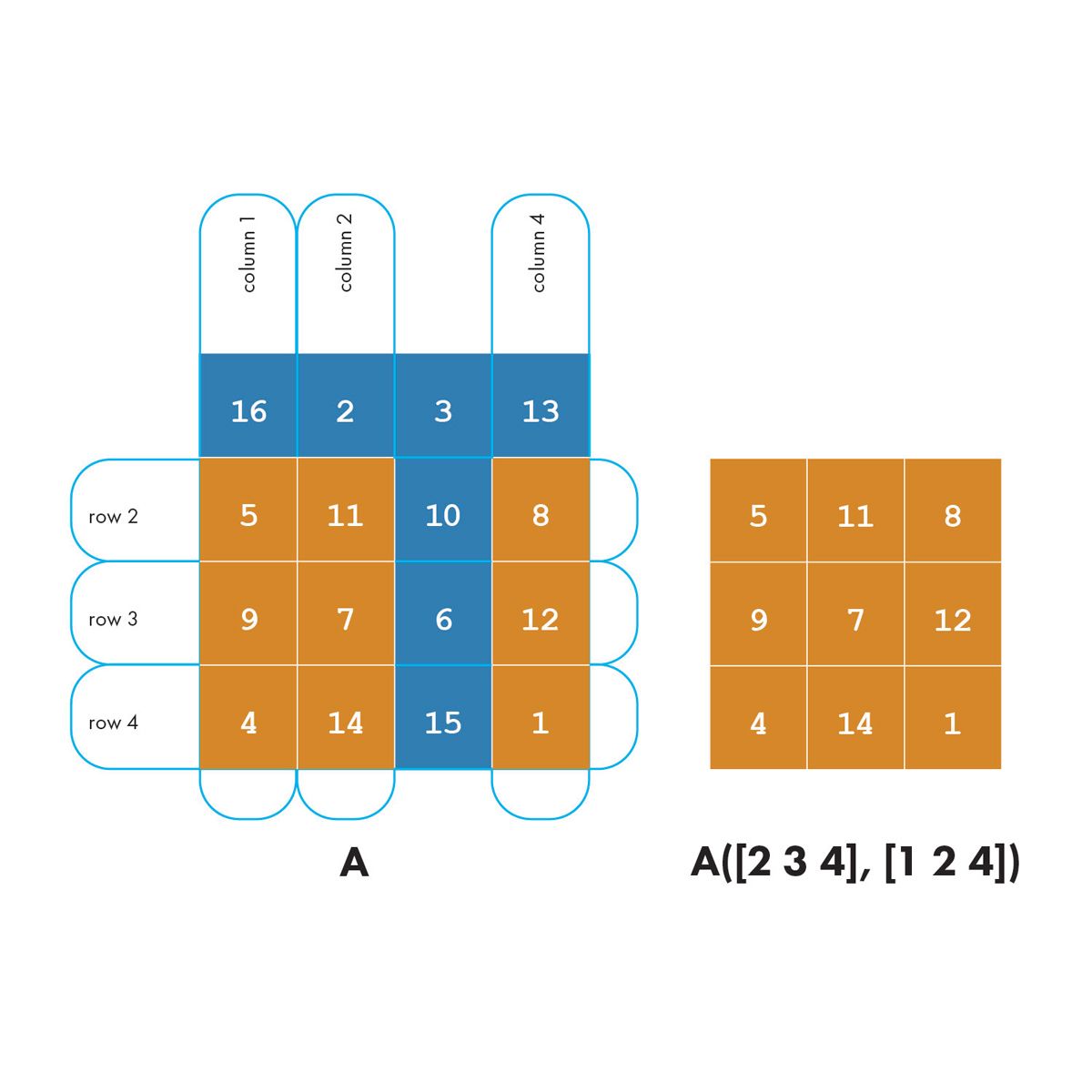
Now consider indexing into a matrix. We’ll use a magic square for our examples.

  A = magic(4)
  A =
          16           2           3          13
           5          11          10           8
           9           7           6          12
           4          14          15           1

Most often, indexing in matrices is done using two subscripts—the first subscript for the rows and the second for the columns.

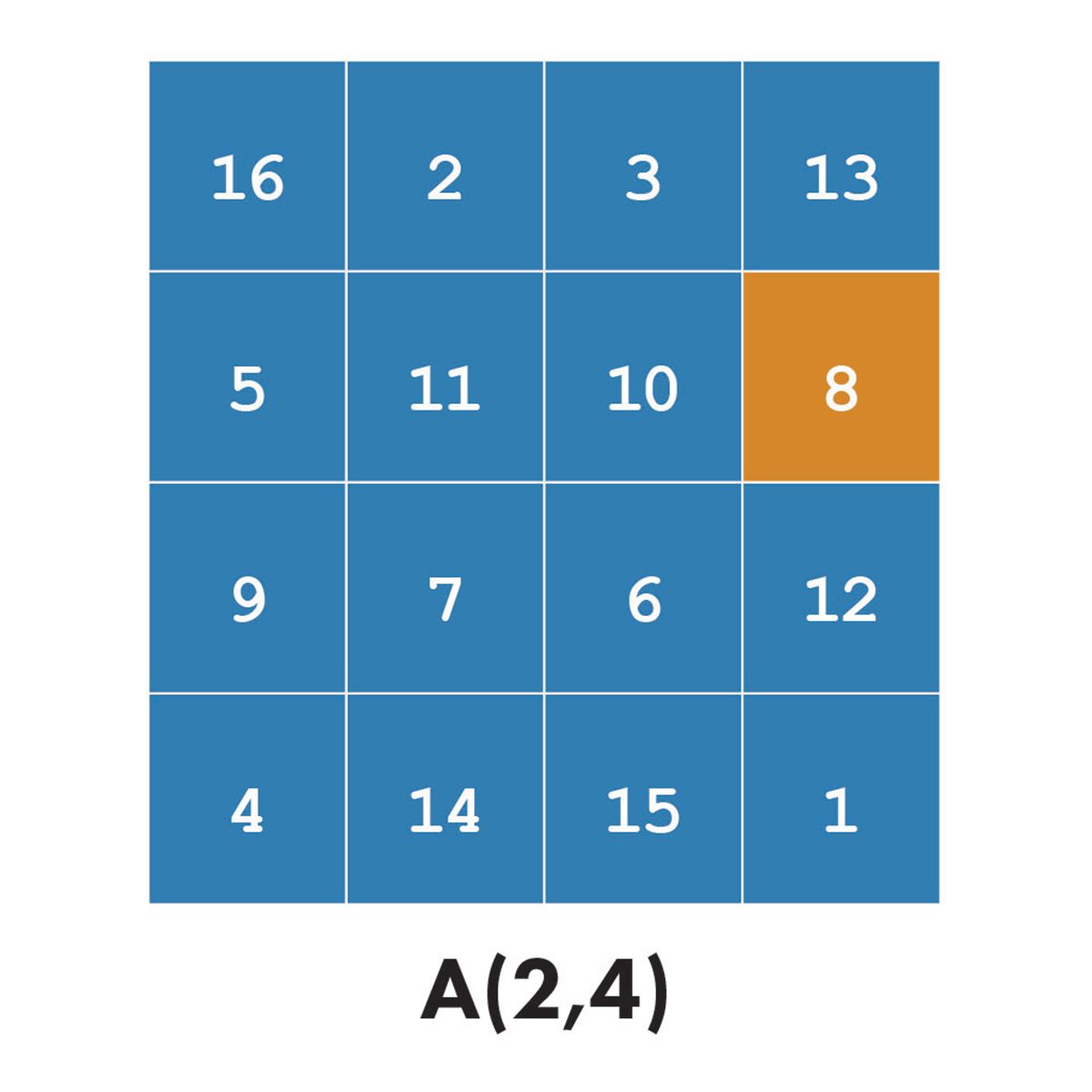
The simplest form picks out a single element.

  A(2,4)   % Extract the element in row 2, column 4
  ans =
       8

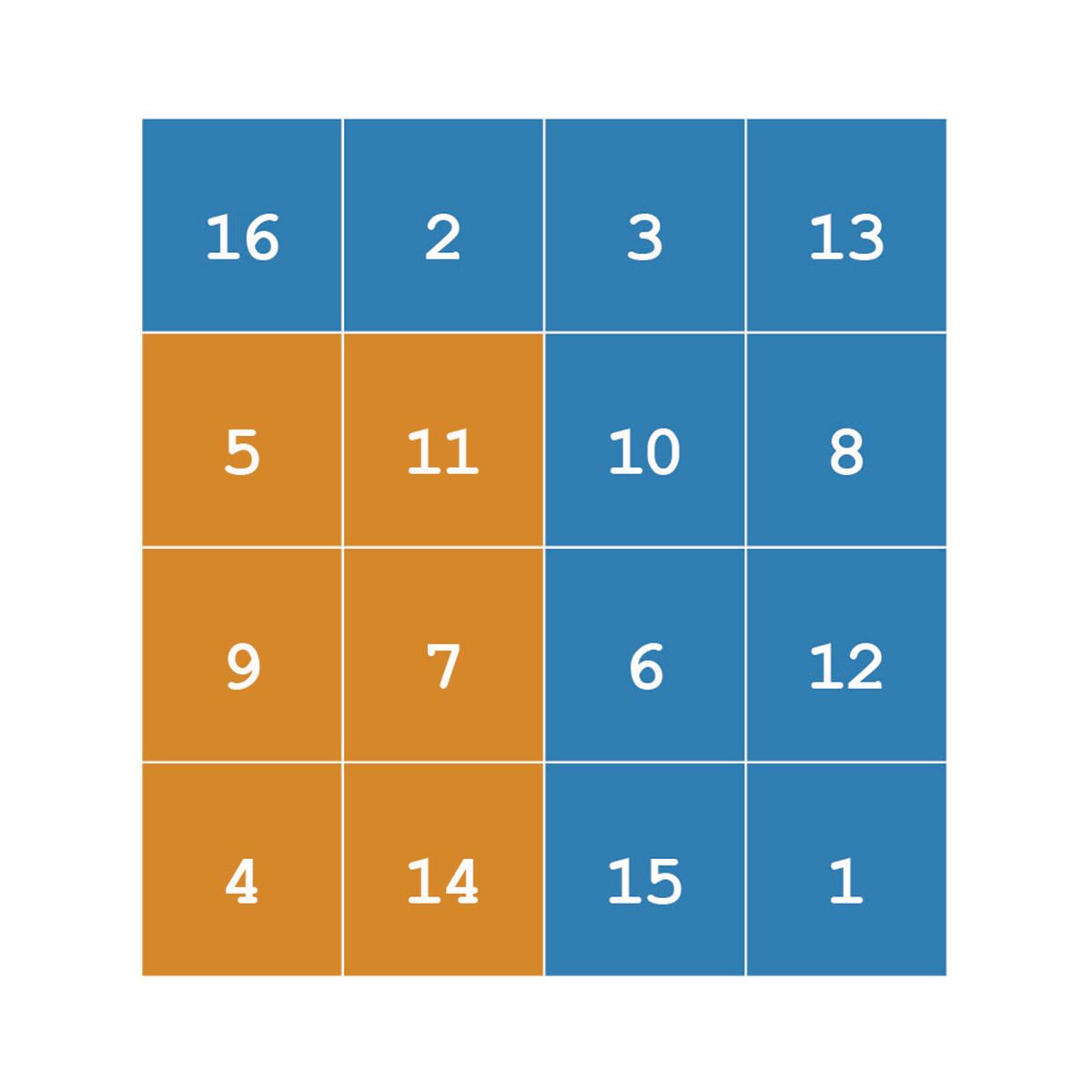
There is sometimes confusion over how to select scattered elements from a matrix. For example, suppose you want to extract the (2,1), (3,2), and (4,4) elements from A.

The expression A([2 3 4], [1 2 4]) won’t do what you want. This diagram illustrates how two-subscript indexing works.

Extracting scattered elements from a matrix requires a different style of indexing, and that brings us to our next topic.

Linear Indexing

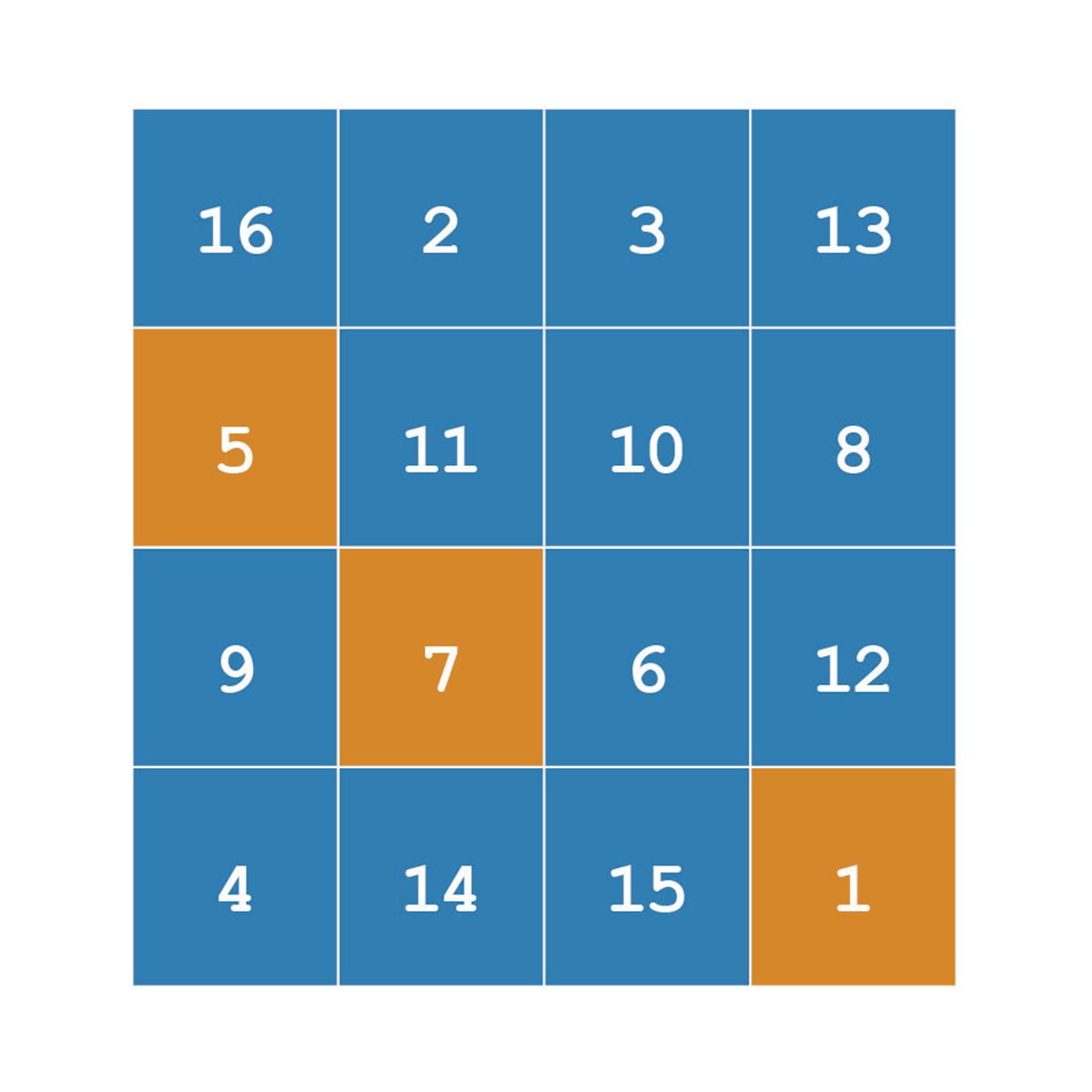
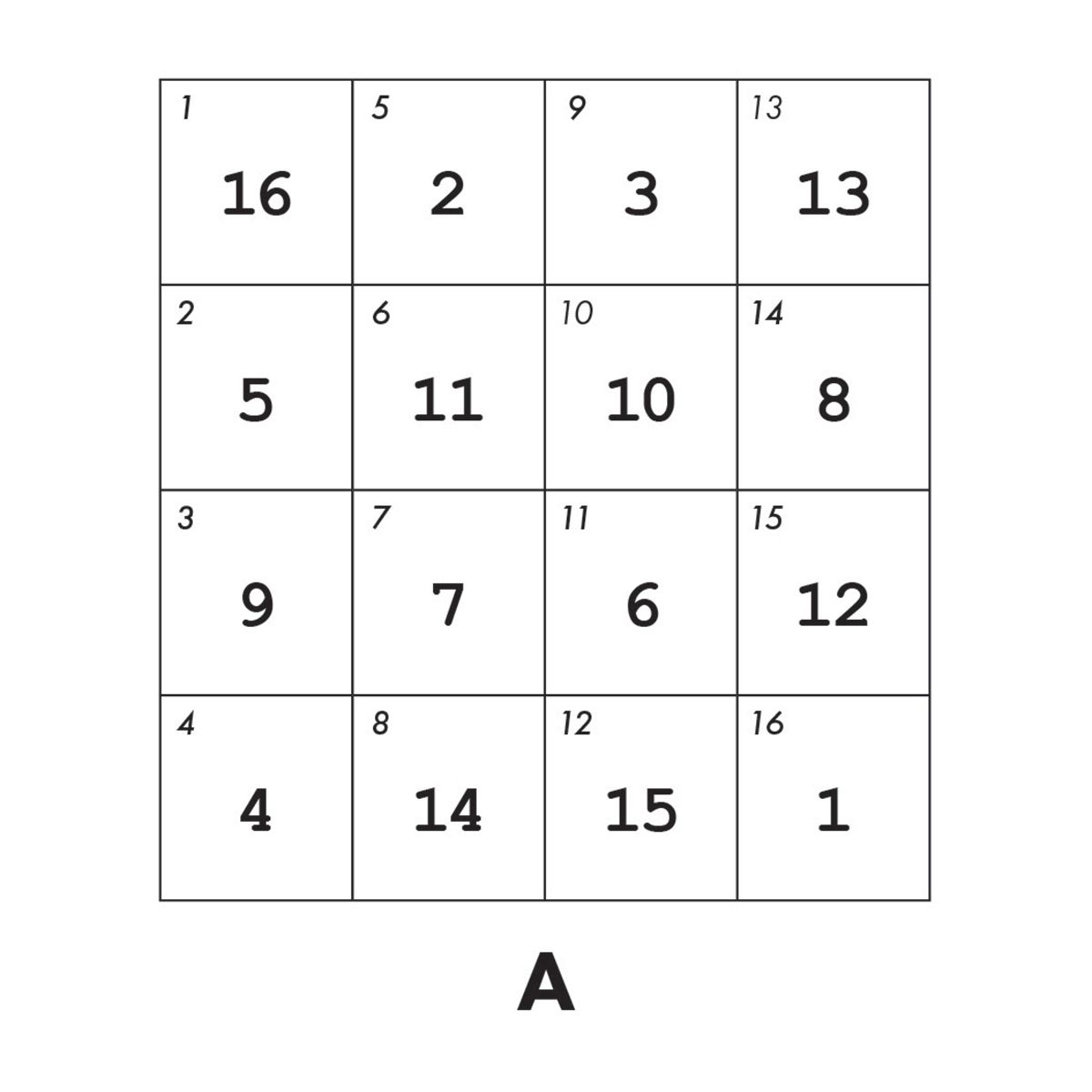
What does this expression A(14) do?

When you index into the matrix A using only one subscript, MATLAB treats A as if its elements were strung out in a long column vector, by going down the columns consecutively, as in:

16
5
9
...
8
12
1

The single subscript can be a vector containing more than one linear index, as in:

  A([6 12 15])
  ans =
      11   15   12

Consider again the problem of extracting just the (2,1), (3,2), and (4,4) elements of A. You can use linear indexing to extract those elements.

  A([2 7 16])
  ans =
      5   7   1

That’s easy to see for this example, but how do you compute linear indices in general? MATLAB provides a function called sub2ind that converts from row and column subscripts to linear indices. You can use it to extract the desired elements this way:

  idx = sub2ind(size(A), [2 3 4], [1 2 4])
  ans =
      2   7   16
  A(idx)
  ans =
      5   7   1

Logical Indexing

Another indexing variation, logical indexing, is a compact and expressive notation that’s useful in many applications, including image processing. In logical indexing, you use a single, logical array for the matrix subscript.

Here is an example of a logical array you could use:

A > 12 

ans =
4×4 logical array

1  0  0  1
0  0  0  0
0  0  0  0
0  1  1  0

These are the locations in the matrix in which the logical expression is true, in this case, any location greater than 12.

Now the expression A(A > 12) extracts the matrix elements corresponding to the nonzero values of the logical array. The output is always in the form of a column vector.

A(A > 12) 

ans =

    16
    14
    15
    13

Many MATLAB functions that start with is return logical arrays and are very useful for logical indexing. For example, you could replace all the NaN elements in an array with another value by using a combination of isnan, logical indexing, and scalar expansion with one line of code.

 B(isnan(B)) = 0

MATLAB has many string array functions that return logical arrays, such as contains, startsWith, and matches. You can use these to operate on text using logical indexing. For example, you could extract all the space program names containing “Skylab.”

>> names

names =

  6×1 string array

    "Mercury"
    "Gemini"
    "Apollo"
    "Skylab"
    "Skylab B"
    "ISS"

>> names(contains(names,"Skylab"))

ans =

  2×1 string array

    "Skylab"
    "Skylab B"

Logical indexing is closely related to the find function. The expression A(A > 5)  is equivalent to A(find(A > 5)). The logical indexing expression is faster for simple cases, but you might use find if you need the index values for something else in the computation. For example, suppose you want to temporarily replace NaN values with zeros, perform some computation, and then put the NaN values back in their original locations. In this example, the computation is two-dimensional filtering using filter2. You do it like this:

  nan_locations = find(isnan(A)); 

  A(nan_locations) = 0; 

  A = filter2(ones(3,3), A); 

  A(nan_locations) = NaN; 

We hope that these examples in the article give you a feel for ways you can express algorithms compactly and efficiently. Including these techniques and related functions in your MATLAB programming repertoire expands your ability to create concise, readable, and vectorized code.

Learn More