Wavelet Changepoint Detection
This example shows how to use wavelets to detect changes in the variance of a process. Changes in variance are important because they often indicate that something fundamental has changed about the data-generating mechanism.
The first example applies wavelet changepoint detection to a very old time series -- the Nile river minima data for the years 622 to 1281 AD. The river-level minima were measured at the Roda gauge near Cairo. Measurements are in meters.
Load and plot the data.
load nileriverminima years = 622:1284; figure plot(years,nileriverminima) title('Nile River Minimum Levels') AX = gca; AX.XTick = 622:100:1222; grid on xlabel('Year') ylabel('Meters')
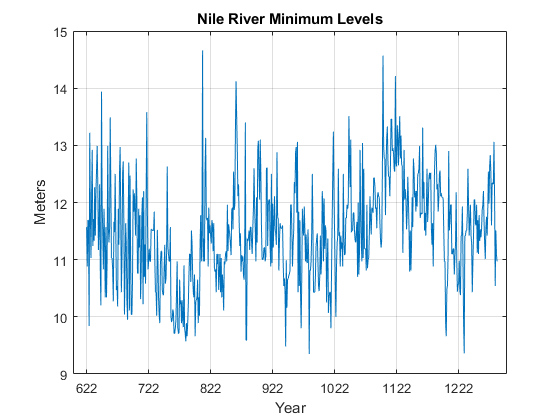
Construction began on a new measuring device around 715 AD. Examining the data prior to and after approximately 722 AD, there appears to be a change in the variability of the data. You can use wavelets to explore the hypothesis that the variability of the measurements has been affected by the introduction of a new measuring device.
Obtain a multiresolution analysis (MRA) of the data using the Haar wavelet.
wt = modwt(nileriverminima,'haar',4); mra = modwtmra(wt,'haar');
Plot the MRA and focus on the level-one and level-two details.
figure subplot(2,1,1) plot(years,mra(1,:)) title('Level 1 Details') subplot(2,1,2) plot(years,mra(2,:)) title('Level 2 Details') AX = gca; AX.XTick = 622:100:1222; xlabel('Years')

Apply an overall change of variance test to the wavelet coefficients.
for JJ = 1:5 pts_Opt = wvarchg(wt(JJ,:),2); changepoints{JJ} = pts_Opt; end cellfun(@(x) ~isempty(x),changepoints,'uni',0)
ans =
1×5 cell array
{[1]} {[0]} {[0]} {[0]} {[0]}
Determine the year corresponding to the detected change of variance.
years(cell2mat(changepoints))
ans = 721
Split the data into two segments. The first segment includes the years 622 to 721 when the fine-scale wavelet coefficients indicate a change in variance. The second segment contains the years 722 to 1284. Obtain unbiased estimates of the wavelet variance by scale.
tspre = nileriverminima(1:100); tspost = nileriverminima(101:end); wpre = modwt(tspre,'haar',4); wpost = modwt(tspost,'haar',4); wvarpre = modwtvar(wpre,'haar',0.95,'table') wvarpost = modwtvar(wpost,'haar',0.95,'table')
wvarpre =
5×4 table
NJ Lower Variance Upper
__ ________ ________ _______
D1 99 0.25199 0.36053 0.55846
D2 97 0.15367 0.25149 0.48477
D3 93 0.056137 0.11014 0.30622
D4 85 0.018881 0.047427 0.26453
S4 85 0.017875 0.0449 0.25044
wvarpost =
5×4 table
NJ Lower Variance Upper
___ ________ ________ _______
D1 562 0.11394 0.13354 0.15869
D2 560 0.085288 0.10639 0.13648
D3 556 0.0693 0.094168 0.13539
D4 548 0.053644 0.081877 0.14024
S4 548 0.24608 0.37558 0.64329
Compare the results.
Vpre = table2array(wvarpre); Vpost = table2array(wvarpost); Vpre = Vpre(1:end-1,2:end); Vpost = Vpost(1:end-1,2:end); Vpre(:,1) = Vpre(:,2)-Vpre(:,1); Vpre(:,3) = Vpre(:,3)-Vpre(:,2); Vpost(:,1) = Vpost(:,2)-Vpost(:,1); Vpost(:,3) = Vpost(:,3)-Vpost(:,2); figure errorbar(1:4,Vpre(:,2),Vpre(:,1),Vpre(:,3),'ko',... 'MarkerFaceColor',[0 0 0]) hold on errorbar(1.5:4.5,Vpost(:,2),Vpost(:,1),Vpost(:,3),'b^',... 'MarkerFaceColor',[0 0 1]) set(gca,'xtick',1.25:4.25) set(gca,'xticklabel',{'2 Year','4 Years','8 Years','16 Years','32 Years'}) grid on ylabel('Variance') title('Wavelet Variance 622-721 and 722-1284 by Scale','fontsize',14) legend('Years 622-721','Years 722-1284','Location','NorthEast')
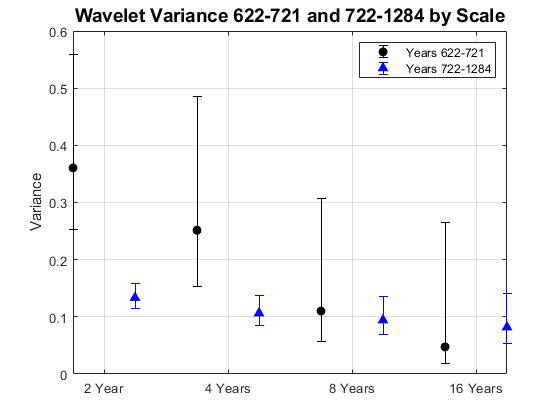
The wavelet variance indicates a significant change in variance between the 622-721 and 722-1284 data over scales of 2 and 4 years.
The above example used the Haar wavelet filter with only two coefficients because of concern over boundary effects with the relatively small time series (100 samples from 622-721). If your data are approximately first or second-order difference stationary, you can substitute the biased estimate using the 'reflection' boundary. This permits you to use a longer wavelet filter without worrying about boundary coefficients. Repeat the analysis using the default 'sym4' wavelet.
wpre = modwt(tspre,4,'reflection'); wpost = modwt(tspost,4,'reflection'); wvarpre = modwtvar(wpre,[],[],'EstimatorType','biased',... 'Boundary','reflection','table'); wvarpost = modwtvar(wpost,[],[],'EstimatorType','biased',... 'Boundary','reflection','table');
Plot the results.
Vpre = table2array(wvarpre); Vpost = table2array(wvarpost); Vpre = Vpre(1:end-1,2:end); Vpost = Vpost(1:end-1,2:end); Vpre(:,1) = Vpre(:,2)-Vpre(:,1); Vpre(:,3) = Vpre(:,3)-Vpre(:,2); Vpost(:,1) = Vpost(:,2)-Vpost(:,1); Vpost(:,3) = Vpost(:,3)-Vpost(:,2); figure errorbar(1:4,Vpre(:,2),Vpre(:,1),Vpre(:,3),'ko','MarkerFaceColor',[0 0 0]) hold on errorbar(1.5:4.5,Vpost(:,2),Vpost(:,1),Vpost(:,3),'b^','MarkerFaceColor',[0 0 1]) set(gca,'xtick',1.25:4.25) set(gca,'xticklabel',{'2 Years','4 Years', '8 Years', '16 Years','32 Years'}) grid on ylabel('Variance') title({'Wavelet Variance 622-721 and 722-1284 by Scale'; ... 'Biased Estimate -- Reflection Boundary'},'fontsize',14) legend('622-721','722-1284','Location','NorthEast') hold off
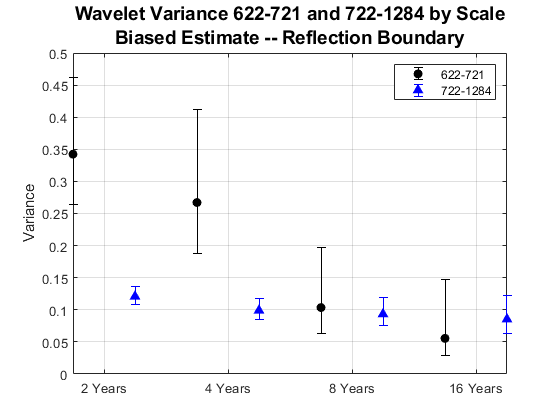
The conclusion is reinforced. There is a significant difference in the variance of the data over scales of 2 and 4 years, but not at longer scales. You can conclude that something has changed about the process variance.
In financial time series, you can use wavelets to detect changes in volatility. To illustrate this, consider the quarterly chain-weighted U.S. real GDP data for 1974Q1 to 2012Q4. The data were transformed by first taking the natural logarithm and then calculating the year-over-year difference. Obtain the wavelet transform (MODWT) of the real GDP data down to level six with the 'db2' wavelet. Examine the variance of the data and compare that to the variances by scale obtained with the MODWT.
load GDPcomponents realgdpwt = modwt(realgdp,'db2',6,'reflection'); gdpmra = modwtmra(realgdpwt,'db2','reflection'); vardata = var(realgdp,1); varwt = var(realgdpwt(:,1:numel(realgdp)),1,2);
In vardata you have the variance for the aggregate GDP time series. In varwt you have the variance by scale for the MODWT. There are seven elements in varwt because you obtained the MODWT down to level six resulting in six wavelet coefficient variances and one scaling coefficient variance. Sum the variances by scale to see that the variance is preserved. Plot the wavelet variances by scale ignoring the scaling coefficient variance.
totalMODWTvar = sum(varwt);
bar(varwt(1:end-1,:))
AX = gca;
AX.XTickLabels = {'[2 4)','[4 8)','[8 16)','[16 32)','[32 64)','[64 128)'};
xlabel('Quarters')
ylabel('Variance')
title('Wavelet Variance by Scale')
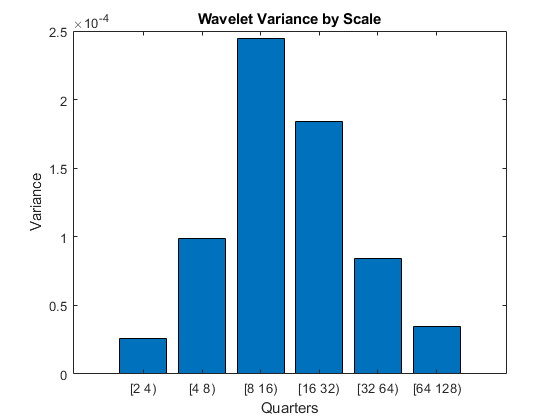
Because this data is quarterly, the first scale captures variations between two and four quarters, the second scale between four and eight, the third between 8 and 16, and so on.
From the MODWT and a simple bar plot, you see that cycles in the data between 8 and 32 quarters account for the largest variance in the GDP data. If you consider the wavelet variances at these scales, they account for 57% of the variability in the GDP data. This means that oscillations in the GDP over a period of 2 to 8 years account for most of the variability seen in the time series.
Plot the level-one details, D1. These details capture oscillations in the data between two and four quarters in duration.
helperFinancialDataExample1(gdpmra(1,:),years,... 'Year over Year Real U.S. GDP - D1')

Examining the level-one details, it appears there is a reduction of variance beginning in the 1980s.
Test the level-one wavelet coefficients for significant variance changepoints.
pts_Opt = wvarchg(realgdpwt(1,1:numel(realgdp)),2); years(pts_Opt)
ans =
1982
There is a variance changepoint identified in 1982. This example does not correct for the delay introduced by the 'db2' wavelet at level one. However, that delay is only two samples so it does not appreciably affect the results.
To assess changes in the volatility of the GDP data pre and post 1982, split the original data into pre- and post-changepoint series. Obtain the wavelet transforms of the pre and post datasets. In this case, the series are relatively short so use the Haar wavelet to minimize the number of boundary coefficients. Compute unbiased estimates of the wavelet variance by scale and plot the result.
tspre = realgdp(1:pts_Opt); tspost = realgdp(pts_Opt+1:end); wtpre = modwt(tspre,'haar',5); wtpost = modwt(tspost,'haar',5); prevar = modwtvar(wtpre,'haar','table'); postvar = modwtvar(wtpost,'haar','table'); xlab = {'[2Q,4Q)','[4Q,8Q)','[8Q,16Q)','[16Q,32Q)','[32Q,64Q)'}; helperFinancialDataExampleVariancePlot(prevar,postvar,'table',xlab) title('Wavelet Variance By Scale') legend('Pre 1982 Q2','Post 1982 Q2','Location','NorthWest')
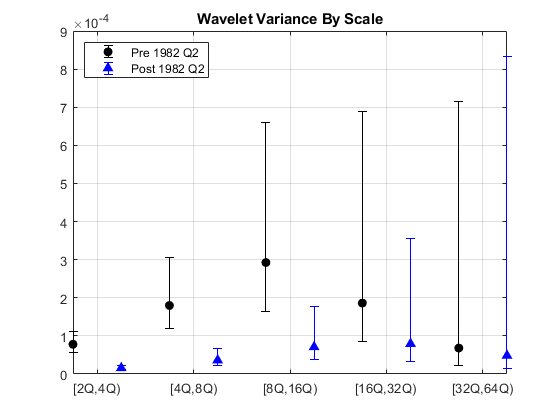
From the preceding plot, it appears there are significant differences between the pre-1982Q2 and post-1982Q2 variances at scales between 2 and 16 quarters.
Because the time series are so short in this example, it can be useful to use biased estimates of the variance. Biased estimates do not remove boundary coefficients. Use a 'db2' wavelet filter with four coefficients.
wtpre = modwt(tspre,'db2',5,'reflection'); wtpost = modwt(tspost,'db2',5,'reflection'); prevar = modwtvar(wtpre,'db2',0.95,'EstimatorType','biased','table'); postvar = modwtvar(wtpost,'db2',0.95,'EstimatorType','biased','table'); xlab = {'[2Q,4Q)','[4Q,8Q)','[8Q,16Q)','[16Q,32Q)','[32Q,64Q)'}; figure helperFinancialDataExampleVariancePlot(prevar,postvar,'table',xlab) title('Wavelet Variance By Scale') legend('Pre 1982 Q2','Post 1982 Q2','Location','NorthWest')
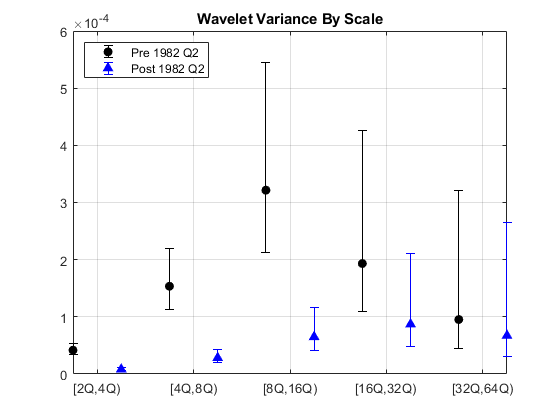
The results confirm our original finding that there is a reduction in volatility over scales from 2 to 16 quarters.
Using the wavelet transform allows you to focus on scales where the change in volatility is localized. To see this, examine a plot of the raw data along with the level-one wavelet details.
subplot(2,1,1) helperFinancialDataExample1(realgdp,years,... 'Year over Year Real U.S. GDP -- Raw Data') subplot(2,1,2) helperFinancialDataExample1(gdpmra(1,:),years,... 'Year over Year Real U.S. GDP -- Wavelet Level 1 Details')

The shaded region is referred to as the "Great Moderation" signifying a period of decreased macroeconomic volatility in the U.S. beginning in the mid 1980s.
Examining the aggregate data, it is not clear that there is in fact reduced volatility in this period. However, the wavelet level-one details uncover the change in volatility.