Smoothing Nonuniformly Sampled Data
This example shows to smooth and denoise nonuniformly sampled data using the multiscale local polynomial transform (MLPT). The MLPT is a lifting scheme (Jansen, 2013) that shares many characteristics of the discrete wavelet transform and works with nonuniformly sampled data.
Many real-world time series have observations that are not recorded at regularly spaced intervals. This may be a result from a nonuniform sampling of the data or from missing or corrupted observations. The discrete wavelet transform (DWT) is a powerful tool for denoising data or performing nonparametric regression, but the classic DWT is defined for uniformly sampled data. The concept of scale, which is central to the DWT, crucially depends on a regular interval between observations.
The lifting scheme (second-generation wavelets) (Jansen & Oonincx, 2005) provides a way to design wavelets and implement the wavelet transform entirely in the time (spatial) domain. While the classic DWT may also be represented by a lifting scheme, lifting is also flexible enough to handle nonuniformly sampled data.
Denoising Data
Load and plot a noisy nonuniformly sampled time series.
load skyline plot(T,y) xlabel('Seconds') grid on

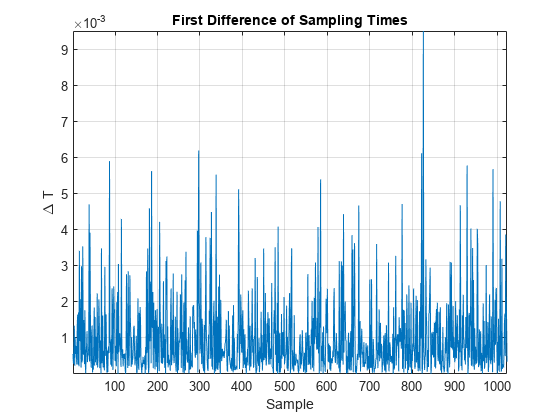
If you plot the difference of the sampling times, you see that the data is nonuniformly sampled.
plot(diff(T)) title('First Difference of Sampling Times') axis tight ylabel('\Delta T') xlabel('Sample') grid on
In this synthetic dataset, you have access to the original noise-free signal. If you plot that data, you see that the data are characterized by smoothly varying features as well as abrupt transient features near 0.07, 0.26, and 0.79 seconds.
plot(T,f) xlabel('Seconds') grid on title('Original (Noise-Free) Data')

In real-world applications, abrupt changes in the data often signify important events. When you denoise such data, it is important not to smooth out the transients. Wavelets typically excel at denoising such data because the wavelets stretch to match longer duration smoothly varying features and shrink to match transients. The MLPT has similar characteristics, but it naturally handles nonuniformly sampled data. Denoise the data using the MLPT.
xden = mlptdenoise(y,T,3); hline = plot(T,[f xden]); grid on hline(1).LineWidth = 2; title('MLPT Denoising')

The MLPT does a good job of denoising the data. The smoothly varying features are well represented and the transients are preserved. In this synthetic data set, you can actually measure the signal-to-noise ratio (SNR) of the denoised version.
SNR = 20*log10(norm(f,2)/norm(xden-f,2)); title(['SNR ' num2str(SNR,'%2.2f') 'dB'])
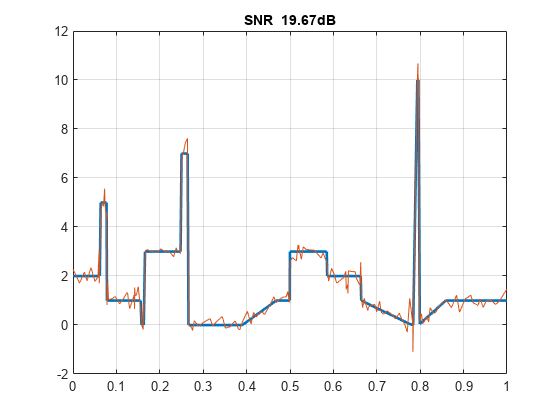
The SNR is almost 20 dB. Of course, you can ignore the fact that the data are nonuniformly sampled and treat the samples as uniformly sampled. Denoise the previous data set using the DWT.
xd = wdenoise(y,3,'Wavelet','bior2.2','DenoisingMethod','SURE','NoiseEstimate','LevelDependent'); SNR = 20*log10(norm(f,2)/norm(xd-f,2)); hline = plot(T,[f xd]); title(['SNR ' num2str(SNR,'%2.2f') 'dB']) grid on hline(1).LineWidth = 2;

Here the DWT does a good job of denoising the data, but it is outperformed by the MLPT, which explicitly takes the nonuniform sampling instants into account.
Compare the wavelet and MLPT denoising results against the Savitzky-Golay method, which implements a local polynomial approximation of the data. The variant of Savitzky-Golay implemented in smoothdata handles uniformly and nonuniformly sampled data.
xdsg = smoothdata(y,'sgolay','degree',4,'samplepoints',T); SNR = 20*log10(norm(f,2)/norm(xdsg-f,2)); hline = plot(T,[f xdsg]); title(['SNR ' num2str(SNR,'%2.2f') ' dB']) grid on hline(1).LineWidth = 2;

Both the classic DWT and the MLPT outperform Savitzky-Golay on this data.
Consider another nonuniformly sampled synthetic dataset.
load nonuniformheavisine plot(t,x) grid on
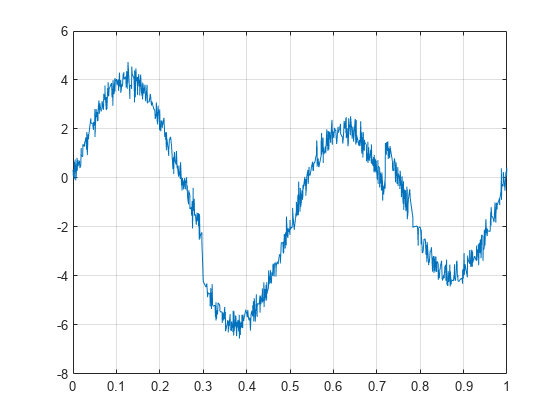
This data is generally smoother than the previous example with the notable exception of two transients at 0.3 and 0.7 seconds. Data like these present a challenge for methods like Savitzky-Golay because a low-order polynomial is required to fit the smoothly oscillating data, while a higher-order polynomial is required to approximate the jumps.
Denoise the data using the MLPT and measure the SNR. Return both the original MLPT coefficients and the denoised coefficients.
[xden,t,wthr,w] = mlptdenoise(x,t,3,'denoisingmethod','SURE'); plot(t,[f xden]) grid on SNR = 20*log10(norm(f,2)/norm(xden-f,2)); title({'MLPT Denoising'; ['SNR ' num2str(SNR,'%2.2f') ' dB']})

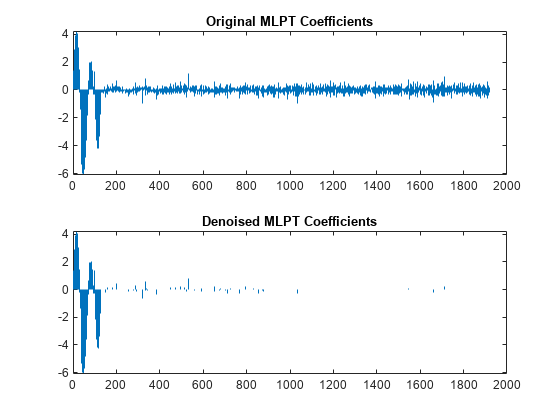
Plot the original and denoised coefficients.
figure subplot(2,1,1) stem(w,'ShowBaseLine','off','Marker','None') title('Original MLPT Coefficients') subplot(2,1,2) stem(wthr,'ShowBaseLine','off','Marker','None') title('Denoised MLPT Coefficients')
Compare the MLPT result with the Savitzky-Golay method.
xdsg = smoothdata(x,'sgolay','degree',4,'samplepoints',t); figure plot(t,[f xdsg]) grid on SNR = 20*log10(norm(f,2)/norm(xdsg-f,2)); title({'Savitzky-Golay Denoising'; ['SNR ' num2str(SNR,'%2.2f') ' dB']})
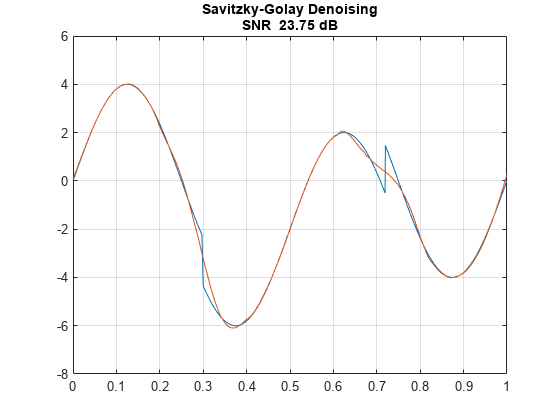
Here the MLPT method significantly outperforms Savitzky-Golay. This is especially evident in the inability of the Savitzky-Golay method to capture the transients near 0.3 and 0.7 seconds.
Nonparametric Regression
In many applications, the goal is to estimate some unknown response function as one or more predictor variables vary. When the exact shape of the response function is unknown, this is an example of nonparametric regression.
A principal objective in these cases is often to obtain a smooth estimate assuming that the unknown response function changes smoothly with changes in the predictor.
As an example of nonparametric regression with nonuniformly sampled data, consider the following data consisting of G-force measurements made on the motorcycle helmet of a crash-test dummy under crash conditions.
load motorcycledata plot(times,gmeasurements) grid on xlabel('Time') ylabel('G-force')

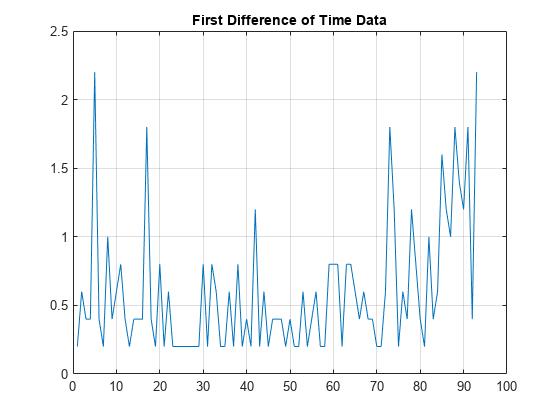
If you plot the difference of the time data, you see that the data is sampled nonuniformly.
plot(diff(times)) title('First Difference of Time Data') grid on
The data are noisy but there appears to be a clear overall trend in the data. Specifically, there is an initial negative G-force experienced which then begins to turn positive over time. The positive rebound continues past 0 and then recovers to baseline. You can use mlptrecon to obtain a nonparametric regression for this data.
[w,t,nj,scalingmoments] = mlpt(gmeasurements,times,'dualmoments',4,... 'primalmoments',4,'prefilter','none'); a4 = mlptrecon('a',w,t,nj,scalingmoments,4,'dualmoments',4); hline = plot(times,[gmeasurements a4]); grid on hline(2).LineWidth = 2; legend('Original Data','Smooth Fit') xlabel('Time') ylabel('G-force') title('G-Force Measurements')

The MLPT approximation at level 4 provides a nice smooth fit to the data that allows you to capture the essential nature of the response without the effect of noise.
Summary
This example demonstrated the multiscale local polynomial transform (MLPT), a lifting scheme which is amenable to nonuniformly sampled data. The MLPT is useful for denoising or nonparametric regression in cases of missing or nonuniformly sampled data. Minimally, it is a useful benchmark for comparison against wavelet denoising techniques designed to work on uniformly sampled data. In other cases, it outperforms conventional wavelet denoising by explicitly taking the nonuniform sampling grid into consideration.
References
Jansen, M. "Multiscale Local Polynomial Smoothing in a Lifted Pyramid for Non-Equispaced Data". IEEE Transactions on Signal Processing. Vol. 61, Number 3, 2013, pp. 545-555.
Jansen, M., and Patrick Oonincx. "Second Generation Wavelets and Applications." London: Springer, 2005.