Use Symbolic Objects to Represent Mathematical Objects

To solve mathematical problems with Symbolic Math Toolbox™, you can define symbolic objects to represent various mathematical objects. This example discusses the usage of these symbolic objects in the Command Window:

• symbolic number

• symbolic scalar variable, function, and expression

• symbolic equation

• symbolic vector and matrix

• symbolic matrix variable

• symbolic matrix function

Symbolic Number

Defining a number as a symbolic number instructs MATLAB^® to treat the number as an exact form instead of using a numeric approximation. For example, use a symbolic number to represent the argument of an inverse trigonometric function $$\theta ={\sin }^{-1}(1/\sqrt{2})$$.

Create the symbolic number $$\text{1/}\sqrt{2}$$ using sym, and assign it to a.

a = sym(1/sqrt(2))

a =
2^(1/2)/2

Find the inverse sine of a. The result is the symbolic number pi/4.

thetaSym = asin(a)

thetaSym =
pi/4

You can convert a symbolic number to variable-precision arithmetic by using vpa. The result is a decimal number with 32 significant digits.

thetaVpa = vpa(thetaSym)

thetaVpa =
0.78539816339744830961566084581988

To convert the symbolic number to a double-precision number, use double. For more information about whether to use numeric or symbolic arithmetic, see Choose Numeric or Symbolic Arithmetic.

thetaDouble = double(thetaSym)

thetaDouble =
0.7854

Symbolic Scalar Variable, Function, and Expression

Defining variables, functions, and expressions as symbolic objects enables you to perform algebraic operations with those symbolic objects, including simplifying formulas and solving equations. For example, use a symbolic scalar variable, function, and expression to represent the quadratic function $$f(x)=x^2+x-2$$. For brevity, a symbolic scalar variable is also called a symbolic variable.

Create a symbolic scalar variable x using syms. You can also use sym to create a symbolic scalar variable. For more information about whether to use syms or sym, see Choose syms or sym Function.

Define a symbolic expression x^2 + x - 2 to represent the right side of the quadratic equation and assign it to f(x). The identifier f(x) now refers to a symbolic function that represents the quadratic function. A symbolic function accepts scalars as input arguments.

syms x
f(x) = x^2 + x - 2

f(x) =
x^2 + x -2

You can then evaluate the quadratic function by providing its input argument inside the parentheses. For example, evaluate f(2).

fVal = f(2)

fVal =
4

You can also solve the quadratic equation $$f(x)=0$$. Use solve to find the roots of the quadratic equation. solve returns the two solutions as a vector of two symbolic numbers.

sols = solve(f)

sols =
-2
 1

Symbolic Equation

Defining a mathematical equation as a symbolic equation enables you to find the solution of the equation. For example, use a symbolic equation to solve the trigonometric problem $$2\sin (t)\cos (t)=1$$.

Create a symbolic function g(t) using syms. Assign the symbolic expression 2*sin(t)*cos(t) to g(t).

syms g(t)
g(t) = 2*sin(t)*cos(t)

g(t) = 
2*cos(t)*sin(t)

To define the equation, use the == operator and assign the mathematical relation g(t) == 1 to eqn. The identifier eqn is a symbolic equation that represents the trigonometric problem.

eqn = g(t) == 1

eqn = 
2*cos(t)*sin(t) == 1

Use solve to find the solution of the trigonometric problem.

sol = solve(eqn)

sol = 
pi/4

Symbolic Vector and Matrix

Use a symbolic vector and matrix to represent and solve a system of linear equations.

$$\begin{array}{c}x+2y=u\\ 4x+5y=v\end{array}$$

You can represent the system of equations as a vector of two symbolic equations. You can also represent the system of equations as a matrix problem involving a matrix of symbolic numbers and a vector of symbolic variables. For brevity, any vector of symbolic objects is called a symbolic vector and any matrix of symbolic objects is called a symbolic matrix.

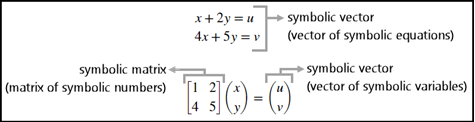
Create two symbolic equations eq1 and eq2. Combine the two equations into a symbolic vector.

syms u v x y
eq1 = x + 2*y == u;
eq2 = 4*x + 5*y == v;
eqns = [eq1, eq2]

eqns =
[x + 2*y == u, 4*x + 5*y == v]

Use solve to find the solutions of the system of equations represented by eqns. solve returns a structure S with fields named after each of the variables in the equations. You can access the solutions using dot notation, as S.x and S.y.

S = solve(eqns);
S.x

ans =
(2*v)/3 - (5*u)/3

S.y

ans =
(4*u)/3 - v/3

Another way to solve the system of linear equations is to convert it to matrix form. Use equationsToMatrix to convert the system of equations to matrix form and assign the output to A and b. Here, A is a symbolic matrix and b is a symbolic vector. Solve the matrix problem by using the matrix division \ operator.

[A,b] = equationsToMatrix(eqns,x,y)

A =
[1, 2]
[4, 5]
 
 
b =
u
v

sols = A\b

sols =
(2*v)/3 - (5*u)/3
    (4*u)/3 - v/3

Symbolic Matrix Variable

Since R2021a

Use symbolic matrix variables to evaluate differentials with respect to vectors.

$$\begin{array}{l}\alpha =y^{\text{T}}Ax\\ \frac{\partial \alpha }{\partial x}=y^{\text{T}}A\\ \frac{\partial \alpha }{\partial y}=x^{\text{T}}{A}^{\text{T}}\end{array}$$

Symbolic matrix variables represent matrices, vectors, and scalars in compact matrix notation. Symbolic matrix variables offer a concise display in typeset and show mathematical formulas with more clarity. You can enter vector- and matrix-based expressions as symbolic matrix variables in Symbolic Math Toolbox.

Create three symbolic matrix variables x, y, and A using the syms command with the matrix syntax. Nonscalar symbolic matrix variables are displayed as bold characters in the Command Window and in the Live Editor.

syms x [4 1] matrix
syms y [3 1] matrix
syms A [3 4] matrix
x
y
A

x =
x

y =
y

A =
A

Define alpha. Find the differential of alpha with respect to the vectors x and y that are represented by the symbolic matrix variables x and y.

alpha = y.'*A*x

alpha =
y.'*A*x

Dx = diff(alpha,x)

Dx =
y.'*A

Dy = diff(alpha,y)

Dy =
x.'*A.'

Substitute y with [1; 2; 3] in Dx and substitute x with [-1; 2; 0; 1] in Dy using subs. When evaluating a symbolic expression, you must substitute values that have the same size as the defined symbolic matrix variables.

Dx = subs(Dx,y,[1; 2; 3])

Dx =
symmatrix([1;2;3]).'*A

Dy = subs(Dy,x,[-1; 2; 0; 1])

Dx =
symmatrix([-1;2;0;1]).'*A.'

Symbolic Matrix Function

Since R2022a

Use a symbolic matrix function to evaluate a matrix polynomial.

$$f(A)=A^2-3A+I_2$$

A symbolic matrix function represents a parameter-dependent function that accepts matrices, vectors, and scalars as input arguments. Symbolic matrix function operates on matrices in compact matrix notation, offering a concise display in typeset and showing mathematical formulas with more clarity. You can enter vector- and matrix-based formulas as symbolic matrix functions in Symbolic Math Toolbox.

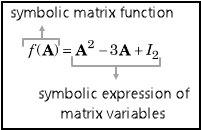
Create a 2-by-2 symbolic matrix variable A using the syms command with the matrix syntax. Create a symbolic matrix function f(A) that accepts A as an input argument using the syms command with the matrix keepargs syntax to keep the previous definition of A.

syms A 2 matrix
syms f(A) 2 matrix keepargs

Assign the polynomial expression to the symbolic matrix function.

f(A) = A^2 - 3*A + 2*eye(2)

f(A) =
 
2*symmatrix(eye(2)) - 3*A + A^2

Evaluate the function for the matrix value A = [1 2; -2 -1]. When evaluating a symbolic matrix function, you must substitute values that have the same size as the defined input arguments.

fEval = f([1 2; -2 -1])

fEval =
 
- 3*symmatrix([1,2;-2,-1]) + symmatrix([1,2;-2,-1])^2 + 2*symmatrix(eye(2))

Convert the evaluated function from the symmatrix data type to the sym data type.

fSym = symmatrix2sym(fEval)

fSym =
[-4, -6]
[ 6,  2]

Comparison of Symbolic Objects

This table compares the symbolic objects that are available in Symbolic Math Toolbox.

Symbolic Object	Examples of MATLAB Command	Size of Symbolic Object	Data Type
Symbolic number	a = 1/sqrt(sym(2)) theta = asin(a) a = 2^(1/2)/2 theta = pi/4	1-by-1	sym
Symbolic scalar variable	syms x y u v	1-by-1	sym
Symbolic function	syms x f(x) = x^2 + x - 2 syms g(t) [1 3] g f(x) = x^2 + x - 2 g(t) = [g1(t), g2(t), g3(t)]	Size of unevaluated function, such as size(g), is 1-by-1. Size of evaluated function, such as size(g(t)), is m-by-n, where m is the row size and n is the column size.	Data type of unevaluated function, such as class(g), is symfun. Data type of evaluated function, such as class(g(t)), is sym.
Symbolic expression	syms x expr = x^2 + x - 2 expr2 = 2*sin(x)*cos(x) expr = x^2 + x - 2 expr2 = 2*cos(x)*sin(x)	1-by-1	sym
Symbolic equation	syms u v x y eq1 = x + 2*y == u eq2 = 4*x + 5*y == v eq1 = x + 2*y == u eq2 = 4*x + 5*y == v	1-by-1	sym
Symbolic vector	syms u v b = [u v] b = [u, v]	1-by-n or m-by-1, where m is the row size and n is the column size	sym
Symbolic matrix	syms A x y A = [x y; x*y y^2] A = [ x, y] [x*y, y^2]	m-by-n, where m is the row size and n is the column size	sym
Symbolic multidimensional array	syms A [2 1 2] A A(:,:,1) = A1_1 A2_1 A(:,:,2) = A1_2 A2_2	sz1-by-sz2-...-szn, where szn is the size of the nth dimension	sym
Symbolic matrix variable (since R2021a)	syms A B [2 3] matrix A B A = A B = B	m-by-n, where m is the row size and n is the column size	symmatrix
Symbolic matrix function (since R2022a)	syms X Y [2 2] matrix syms f(X,Y) [2 2] matrix keepargs f(X,Y) = X*Y - Y*X f(X, Y) = X*Y - Y*X	Size of unevaluated matrix function, such as size(f), is 1-by-1. Size of evaluated function, such as size(f(X,Y)), is m-by-n, where m is the row size and n is the column size.	Data type of unevaluated matrix function, such as class(f), is symfunmatrix. Data type of evaluated function, such as class(f(X,Y)), is symmatrix.