Find Almost Integers with High-Precision Arithmetic
Algorithms for finding integer relations [1], such as the PSLQ algorithm, require high-precision arithmetic to produce accurate results. The higher the precision of the inputs to the algorithm, the greater the level of confidence that the algorithm can find an integer relation that is not just a numerical artifact. The PSLQ algorithm can encounter false positives, such as those caused by almost integers.
This example shows how to find almost integers, or numbers that are very close to integers, using variable-precision arithmetic in Symbolic Math Toolbox™. This example searches for almost integers (or near-integers) that have the form or for the integers .
First, consider a well-known example of an almost integer [2] that is the real number . Create this real number as an exact symbolic number.
r = exp(pi*sqrt(sym(163)))
r =
Evaluate this number with variable-precision arithmetic using vpa. By default, vpa calculates values to 32 significant digits.
vpa(r)
ans =
You can change the number of significant digits to a higher precision by using digits. Evaluate the same number to 40 significant digits.
digits(40) vpa(r)
ans =
This number is very close to an integer. Find the difference between this real number and its nearest integer. Use vpa to evaluate this result to 40 significant digits.
dr = vpa(round(r)-r)
dr =
Next, search for almost integers that have the form for the integers . Create these numbers as exact symbolic numbers.
A = exp(pi*sqrt(sym(1:200)));
Set the number of significant digits to the number of digits in the integer part of plus 20 decimal points.
d = log10(A(end)); digits(ceil(d) + 20)
Evaluate the differences between this series of numbers and their nearest integers. Find the almost integers with rounding errors that are less than 0.0001. Show the results in exact symbolic form.
B = vpa(round(A)-A); A_nearint = A(abs(B)<0.0001)'
A_nearint =
Evaluate the almost integers with a precision of at least 20 decimal points.
A_nearint = vpa(A_nearint)
A_nearint =
Plot the histogram of the differences to show their distribution. The distribution has many occurrences of differences that are close to zero, where the form is an almost integer.
histogram(double(B),50)
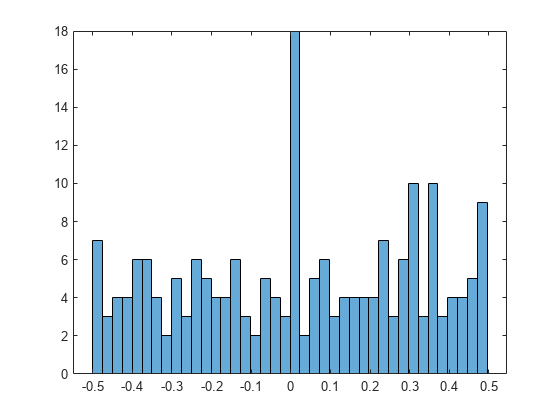
Next, search for almost integers that have the form for the integers . Create these numbers as exact symbolic numbers.
A = exp(sym(pi)*(1:200));
Set the number of significant digits to the number of digits in the integer part of plus 20 decimal points.
d = log10(A(end)); digits(ceil(d) + 20)
Evaluate the differences between this series of numbers and their nearest integers. Find the almost integers with rounding errors that are less than 0.0001. The result is an empty sym array, which means there is no almost integer that satisfies this condition.
B = vpa(round(A)-A); A_nearint = A(abs(B)<0.0001)
A_nearint = Empty sym: 1-by-0
Plot the histogram of the differences. The histogram is relatively evenly distributed and shows that the form does not have many occurrences of almost integers. For this specific example, there is no almost integer with a rounding error that is less than 0.0001.
histogram(double(B),50)

Finally, restore the default precision of 32 significant digits for further calculations.
digits(32)
References
[1] “Integer Relation Algorithm.” In Wikipedia, April 9, 2022. https://en.wikipedia.org/w/index.php?title=Integer_relation_algorithm&oldid=1081697113.
[2] “Almost Integer.” In Wikipedia, December 4, 2021. https://en.wikipedia.org/w/index.php?title=Almost_integer&oldid=1058543590.