LPBoost and TotalBoost for Small Ensembles
This example shows how to obtain the benefits of the LPBoost and TotalBoost algorithms. These algorithms share two beneficial characteristics:
They are self-terminating, which means you do not have to figure out how many members to include.
They produce ensembles with some very small weights, enabling you to safely remove ensemble members.
Load the data
Load the ionosphere data set.
load ionosphereCreate the classification ensembles
Create ensembles for classifying the ionosphere data using the LPBoost, TotalBoost, and, for comparison, AdaBoostM1 algorithms. It is hard to know how many members to include in an ensemble. For LPBoost and TotalBoost, try using 500. For comparison, also use 500 for AdaBoostM1.
The default weak learners for boosting methods are decision trees with the MaxNumSplits property set to 10. These trees tend to fit better than tree stumps (with 1 maximum split) and may overfit more. Therefore, to prevent overfitting, use tree stumps as weak learners for the ensembles.
rng('default') % For reproducibility T = 500; treeStump = templateTree('MaxNumSplits',1); adaStump = fitcensemble(X,Y,'Method','AdaBoostM1','NumLearningCycles',T,'Learners',treeStump); totalStump = fitcensemble(X,Y,'Method','TotalBoost','NumLearningCycles',T,'Learners',treeStump); lpStump = fitcensemble(X,Y,'Method','LPBoost','NumLearningCycles',T,'Learners',treeStump); figure plot(resubLoss(adaStump,'Mode','Cumulative')); hold on plot(resubLoss(totalStump,'Mode','Cumulative'),'r'); plot(resubLoss(lpStump,'Mode','Cumulative'),'g'); hold off xlabel('Number of stumps'); ylabel('Training error'); legend('AdaBoost','TotalBoost','LPBoost','Location','NE');

All three algorithms achieve perfect prediction on the training data after a while.
Examine the number of members in all three ensembles.
[adaStump.NTrained totalStump.NTrained lpStump.NTrained]
ans = 1×3
500 52 68
AdaBoostM1 trained all 500 members. The other two algorithms stopped training early.
Cross validate the ensembles
Cross validate the ensembles to better determine ensemble accuracy.
cvlp = crossval(lpStump,'KFold',5); cvtotal = crossval(totalStump,'KFold',5); cvada = crossval(adaStump,'KFold',5); figure plot(kfoldLoss(cvada,'Mode','Cumulative')); hold on plot(kfoldLoss(cvtotal,'Mode','Cumulative'),'r'); plot(kfoldLoss(cvlp,'Mode','Cumulative'),'g'); hold off xlabel('Ensemble size'); ylabel('Cross-validated error'); legend('AdaBoost','TotalBoost','LPBoost','Location','NE');
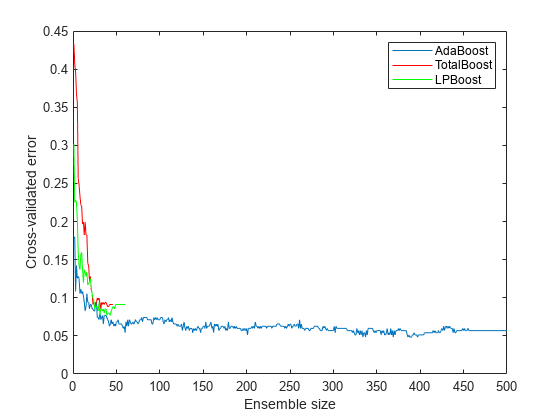
The results show that each boosting algorithm achieves a loss of 10% or lower with 50 ensemble members.
Compact and remove ensemble members
To reduce the ensemble sizes, compact them, and then use removeLearners. The question is, how many learners should you remove? The cross-validated loss curves give you one measure. For another, examine the learner weights for LPBoost and TotalBoost after compacting.
cada = compact(adaStump); clp = compact(lpStump); ctotal = compact(totalStump); figure subplot(2,1,1) plot(clp.TrainedWeights) title('LPBoost weights') subplot(2,1,2) plot(ctotal.TrainedWeights) title('TotalBoost weights')

Both LPBoost and TotalBoost show clear points where the ensemble member weights become negligible.
Remove the unimportant ensemble members.
cada = removeLearners(cada,150:cada.NTrained); clp = removeLearners(clp,60:clp.NTrained); ctotal = removeLearners(ctotal,40:ctotal.NTrained);
Check that removing these learners does not affect ensemble accuracy on the training data.
[loss(cada,X,Y) loss(clp,X,Y) loss(ctotal,X,Y)]
ans = 1×3
0 0 0
Check the resulting compact ensemble sizes.
s(1) = whos('cada'); s(2) = whos('clp'); s(3) = whos('ctotal'); s.bytes
ans = 569228
ans = 227374
ans = 151414
The sizes of the compact ensembles are approximately proportional to the number of members in each.
See Also
fitcensemble | resubLoss | crossval | kfoldLoss | compact | loss | removeLearners