Perform an Online Harmonic Analysis Using the Simscape Spectrum Analyzer Block
Harmonic Distortion
Nonlinear loads create power distortion in the form of harmonics, that is, voltages and currents that are multiples of the fundamental frequency. Harmonic waveforms can result in energy losses through heat dissipation and in reduced power quality. They can also cause equipment to malfunction or to become damaged. Standards development organizations such as the Institute of Electrical and Electronics Engineers (IEEE) and the International Electrotechnical Commission (IEC) define the recommended limits for harmonic content in electric power systems.
This example shows how to examine harmonic distortion in your model using offline, that is after simulation, and online, that is during simulation, analyses. The offline analysis uses the Simscape™ Electrical™ harmonic analysis functions and helps you to determine configuration settings for, and verify the results of, the online analysis. The online analysis uses the Simscape Spectrum Analyzer block.
Prerequisite
This example requires a simulation log variable in your MATLAB® workspace. The model in this example is configured to log Simscape data for the whole model for the entire simulation time.
To learn how to determine if a model is configured to log simulation data, see Examine the Simulation Data Logging Configuration of a Model.
Perform an Offline Harmonic Analysis
Open the model. At the MATLAB Command Window, enter:
openExample("simscapeelectrical/CompositeRectifierExample")
The example model contains a three-phase rectifier. The model also contains a Selector block that outputs only the a-phase from three-phase current signal that it receives from the PS-Simulink Converter block.
Simulate the model.
sim("CompositeRectifier")View the time-domain results. Open the Scope block.
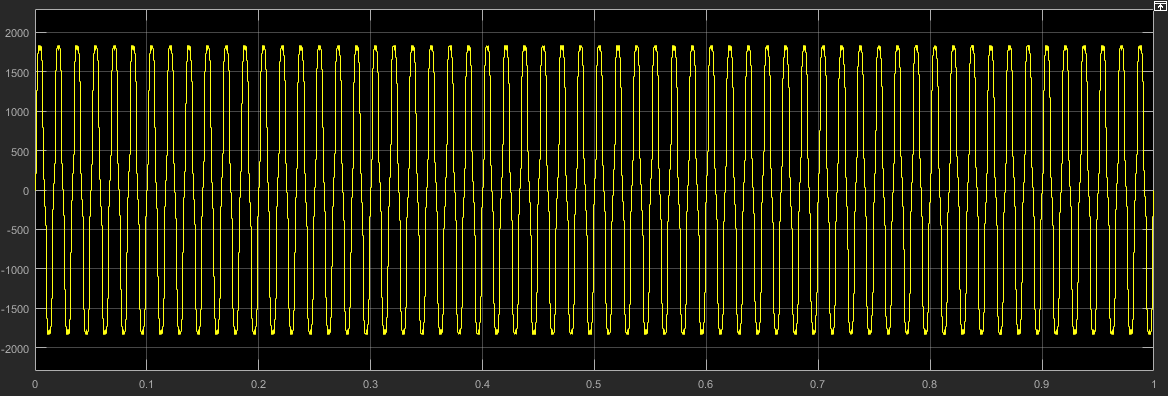
The time domain analysis shows that the rectifier is converting the voltage, but it does not include any information about the frequencies in the signal.
Determine configuration settings and calculate the expected results for an online harmonic analysis. Perform an offline harmonic analysis.
The Simscape Electrical harmonic analysis functions require that you use a fixed-step solver. Determine the solver type and sample time for the model. To turn on sample-time highlighting, in the Simulink® editor menu bar, select Debug > Information Overlays > Sample Time > Colors.
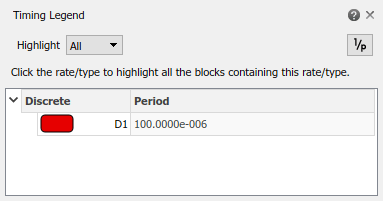
The model is running at a discrete rate, therefore it is using a fixed-step solver, with a sample time of 1e-4 s.
Use the
ee_getHarmonicsfunction to calculate the harmonic order, the harmonic magnitude, and the fundamental frequency based on the voltage source currents.[harmonicOrder,harmonicMagnitude,fundamentalFrequency] = ... ee_getHarmonics(simlog_CompositeRectifier.Voltage_Source.I);
Performing an online harmonic analysis using the Spectrum Analyzer block requires that you specify a value for maximum harmonic order and the resolution bandwidth (RBW). The RBW depends on the fundamental frequency.
Extract and display the maximum harmonic order and the fundamental frequency:
disp(['Maximum Harmonic Order = ', num2str(max(harmonicOrder))]) disp(['Fundamental Frequency = ', num2str(fundamentalFrequency)])
Maximum Harmonic Order = 30 Fundamental Frequency = 60
Determine the peak value of the fundamental frequency. This value is useful for filtering out negligible harmonics and for verifying the results of the offline analyses.
fundamentalPeak = harmonicMagnitude(harmonicOrder==1); disp(['Peak value of fundamental = ', num2str(fundamentalPeak),' A']);
Peak value of fundamental = 1945.806 A
Filter out small harmonics by identifying and keeping harmonics that are greater than one thousandth of the fundamental peak frequency.
threshold = fundamentalPeak ./ 1e3; aboveThresold = harmonicMagnitude > threshold; harmonicOrder = harmonicOrder(aboveThresold)'; harmonicMagnitude = harmonicMagnitude(aboveThresold)';
Display the harmonic data in a MATLAB table.
harmonicRms = harmonicMagnitude./sqrt(2); harmonicPct = 100.*harmonicMagnitude./harmonicMagnitude(harmonicOrder == 1); harmonicTable = table(harmonicOrder,... harmonicMagnitude,... harmonicRms,... harmonicPct,... 'VariableNames',{'Order','Magnitude','RMS','Percentage'}); display(harmonicTable);
harmonicTable = 10×4 table Order Magnitude RMS Percentage _____ _________ ______ __________ 1 1945.8 1375.9 100 5 218.86 154.75 11.248 7 105.83 74.835 5.439 11 85.135 60.2 4.3753 13 57.599 40.729 2.9602 17 50.417 35.65 2.5911 19 37.612 26.596 1.933 23 33.859 23.942 1.7401 25 26.507 18.743 1.3622 29 23.979 16.955 1.2323Calculate the total harmonic distortion (THD) percentage using the
ee_calculate_ThdPercentfunction.thdPercent = ee_calculateThdPercent(harmonicOrder,harmonicMagnitude); disp(['Total Harmonic Distortion Percentage = ' num2str(thdPercent),' %']);
Total Harmonic Distortion percentage = 14.1721 %
Perform an Online Harmonic Analysis
In the Simulink editor that contains the
CompositeRectifiermodel, replace the Scope block with a Spectrum Analyzer block from the Simscape Utilities Library:Delete the Scope block.
Left-click within the block diagram.
After the search icon appears, type
spec, and then from the list, select theSpectrum Analyzerfrom theUtilitieslibrary.Connect the Spectrum Analyzer block to the output signal from the Subsystem i.
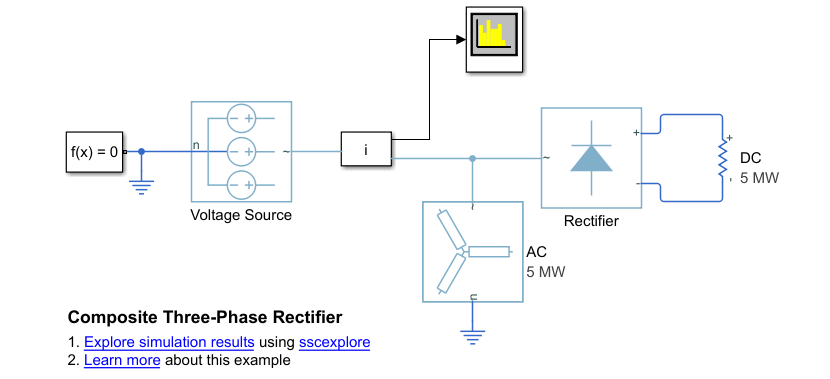
Configure the Spectrum Analyzer block using the Spectrum Settings panel.
Open the Spectrum Analyzer.
Configure the block to display the root mean square (RMS) of the frequency. Under the Analyzer tab, in the Views section, click Spectrum and select RMS.
Determine the value to specify for the resolution bandwidth (RBW) using this equation:
where,
NENBW is the normalized effective noise bandwidth, a factor of the windowing method used. The Hanning (Hann) window has an NENBW value of approximately 1.5.
f is the fundamental frequency.
N is the number of periods.
RBW is the resolution bandwidth in Hz.
For a fundamental frequency of 60 Hz over 10 periods, using a Hann window,
Under the Analyzer tab, in the Bandwidth section, set RBW (Hz) to
9.Under the Estimation tab, in the Window Options section, set Overlap (%) to
90.Specify the maximum number of peaks for the analyzer to display. Under the Measurements tab, in the Peaks section, click Peak Finder
 . Then set Max Num of
Peaks to
. Then set Max Num of
Peaks to 30. This value is based on the maximum harmonic order as indicated by the offline analysis.Set the number of harmonics to use for measuring harmonic distortion. Specify a number that captures the largest harmonic order that the offline analysis captures. Under the Measurements tab, in the Distortion section, click Distortion
 . Then set Num
Harmonics to
. Then set Num
Harmonics to 30.
Simulate the model.
sim("CompositeRectifier")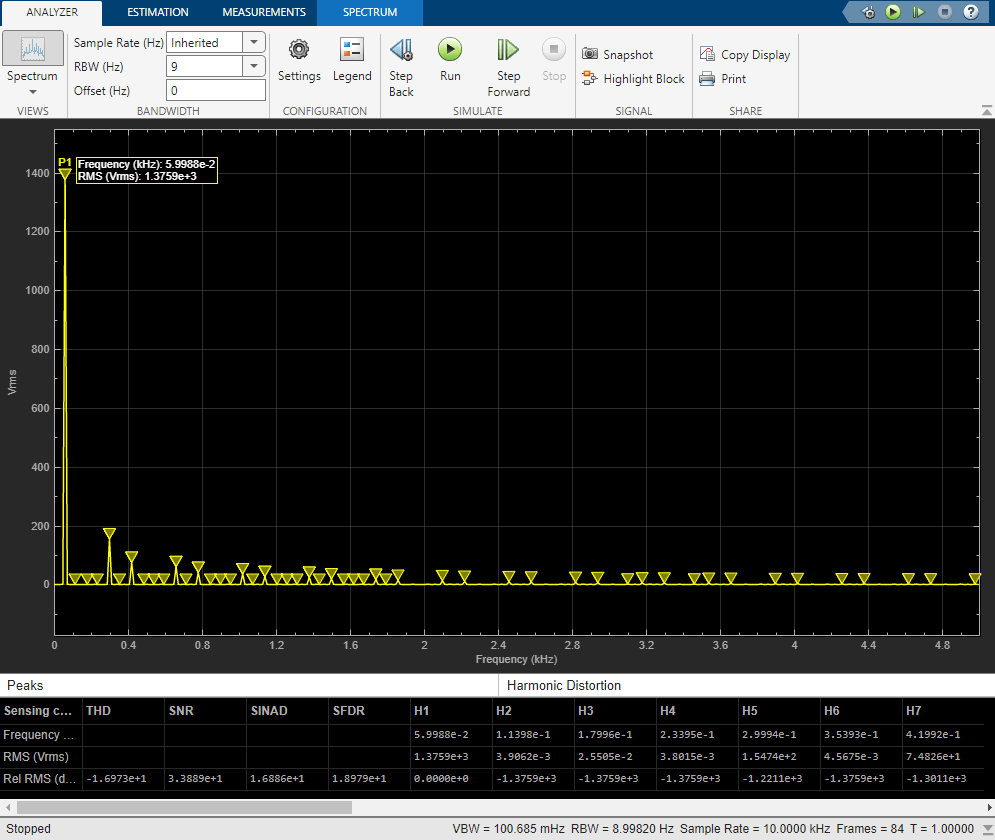
The fundamental peak power is 1375.89 Vrms at 0.06 kHz (60 Hz). These results agree with the results from the offline harmonic analysis.