Induction Machine Direct Torque Control with Space Vector Modulator
Induction machine DTC structure with SVM
Libraries:
Simscape /
Electrical /
Control /
Induction Machine Control
Description
The Induction Machine Direct Torque Control with Space Vector Modulator implements an induction machine direct torque control structure (DTC) with space vector modulator (SVM). Use this block to generate the gate pulses for an inverter controlling an induction machine. This diagram shows the architecture of the block.
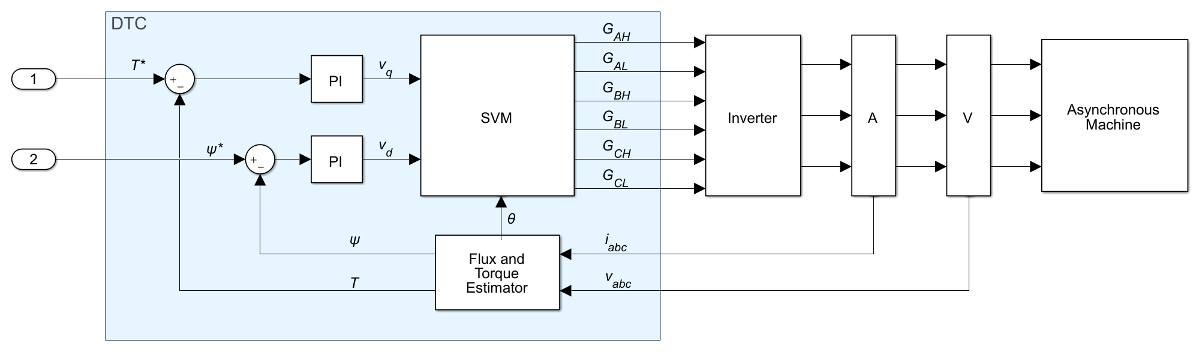
In the diagram:
You provide the reference torque, T*, and flux, ψ*.
The Flux and Torque Estimator estimates the actual torque, T, and flux, ψ from the measured phase currents, iabc, and voltages, vabc.
Two PI controllers determine the reference d and q voltages, vd and vq, from the flux and torque errors, respectively.
The SVM generates the gates pulses, Gij, required to control an inverter driving the induction machine. Subscript i corresponds to the phase (a, b, or c). Subscript j corresponds to the high, H, or low, L, signal.
Flux and Torque Estimator
To estimate the torque and flux, the block discretizes the machine voltage equations in the stationary ɑβ reference frame using the backward Euler method. The discrete-time equations for stator fluxes in the ɑβ frame are:
Where:
vɑ and vβ are the ɑ- and β-axis voltages, respectively.
iɑ and iβ are the ɑ- and β-axis currents, respectively.
Ψɑ and Ψβ are the ɑ- and β-axis stator fluxes, respectively.
Rs is the stator resistance.
The block calculates the torque and total stator flux as:
Where:
p is the number of pole pairs.
Ψs is the total stator flux.
Space Vector Modulator
The SVM converts the desired voltages into gate pulses, which you use to control an inverter. This figure shows possible switching states of a three-phase inverter.
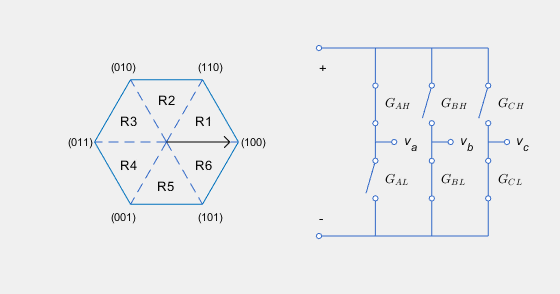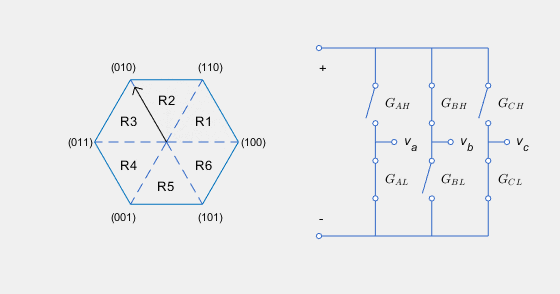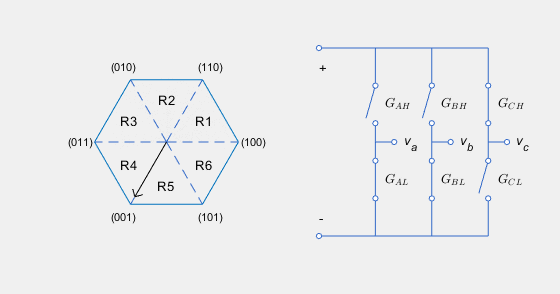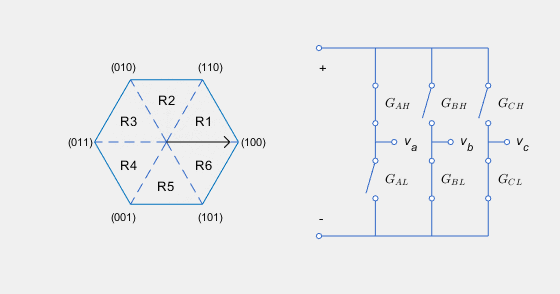
The hexagon represents the space vector diagram. Each of the six vertices represents a possible switching state (GAH,GBH,GCH) of the three-phase inverter. Each low gate takes the opposite state as its corresponding high gate. The inverter diagram illustrates the current state.
The rotating vector in the space vector diagram corresponds to the complex reference voltage vector, which rotates at the desired electrical frequency of the machine. In reality, the switching frequency is much faster than this electrical frequency. As a result, the inverter switches continually between the two states enclosing its current region Ri, and the zero state corresponding to (0,0,0), to generate the desired voltages.
To learn about the implementation of this method, see the PWM Generator (Three-phase, Two-level) block.
Examples
Ports
Input
Output
Parameters
References
[1] Buja, G. S., and M. P Kazmierkowski. "Direct Torque Control of PWM Inverter-Fed AC Motors—A Survey." IEEE Transactions on Industrial Electronics 51, no. 4, (2004): 744 - 757.
Extended Capabilities
Version History
Introduced in R2018a
See Also
Blocks
- Induction Machine Current Controller | Induction Machine Direct Torque Control | Induction Machine Direct Torque Control (Single-Phase) | Induction Field-Oriented Control | Induction Machine Field-Oriented Control (Single-Phase) | Induction Machine Induction Flux Observer | Induction Machine Scalar Control