Parameter Estimation with Constraints

Since R2023b

This example shows how to perform parameter estimation while also imposing constraints the model needs to obey. In this example, you estimate the parameters of an engine throttle system.

Engine Throttle Model

The throttle controls the air flow into the intake manifold of an engine. The throttle body contains a valve that opens when the driver presses down on the accelerator pedal. This lets more air enter the cylinders.

A DC motor controls the opening angle of the butterfly valve. There is also a spring attached to the valve to return it to its closed position when the DC motor is de-energized. The amount of rotation of the valve is limited to approximately 90 degrees. Therefore, if a large command input is applied to the motor, the valve hits the hard stops preventing it from rotating further.

The DC motor is modeled as a torque gain and a time-delay input with parameters Kt and input_delay. The butterfly valve is modeled as a mass-spring-damper system with parameters J, c and k. This system is augmented with hard stops to limit the valve opening to 90 degrees. The model components are known, however the parameter values of the system are not known accurately and need to be estimated. Additionally, the torque produced by the motor is bounded. Therefore, you need to impose this constraint on the parameter estimation process.

Open the model.

open_system('spe_engine_throttle')

Specify Model Parameters to Estimate

The parameters to estimate are:

• Motor delay input_delay.

• Throttle moment of inertia J, damping c, and spring constant, k.

p = sdo.getParameterFromModel('spe_engine_throttle',{'J','c','input_delay','k'});

Set initial guesses for these parameters.

p(1).Value = 0.2;
p(2).Value = 9;
p(3).Value = 0.01;
p(4).Value = 18;

Since these are all physical parameters, specify the minimum values as 0 or positive.

p(1).Minimum = 0;
p(2).Minimum = 0;
p(3).Minimum = 1e-6;
p(3).Maximum = 0.1;
p(4).Minimum = 0;

Specify Constraints

The motor torque is bounded and this constraint must be satisfied during parameter tuning. Describe this constraint so you can impose it as a requirement during parameter estimation.

Requirements = struct;
boundMagnitude = 15;
Requirements.SignalBound = sdo.requirements.SignalBound(...
    'BoundTimes',      [0  0.5], ...
    'BoundMagnitudes', boundMagnitude*[1 1], ...
    'Type',            '<=');
Requirements.SignalBound2 = sdo.requirements.SignalBound(...
    'BoundTimes',      [0  0.5], ...
    'BoundMagnitudes', -boundMagnitude*[1 1], ...
    'Type',            '>=');

To evaluate the requirement, log the model signals on which these requirements are based. Specify the model signals to log during model simulation.

Sig_Info = Simulink.SimulationData.SignalLoggingInfo;
Sig_Info.BlockPath = 'spe_engine_throttle/Throttle/Velocity';
Sig_Info.LoggingInfo.LoggingName = 'Sig';
Sig_Info.LoggingInfo.NameMode = 1;

Define a simulator, which is runs the model with different parameter values. Add the signal logging specification to the simulator.

Simulator = sdo.SimulationTest('spe_engine_throttle');
Simulator.LoggingInfo.Signals = Sig_Info;

Define Estimation Experiments

The estimation experiment compares the measured data with the model output, at the corresponding model signal. Define an experiment to associate measured data with the model signal.

Time = time1;
MotorCommand = input1;
ThrottlePosition = position1;
EstimationData = sdo.Experiment('spe_engine_throttle');

Specify the measured input data and associate it with the corresponding model input.

EstimationData_Sig_Input = Simulink.SimulationData.Signal;
EstimationData_Sig_Input.Values    = timeseries(MotorCommand,Time);
EstimationData_Sig_Input.BlockPath = 'spe_engine_throttle/Input';
EstimationData_Sig_Input.PortType  = 'inport';
EstimationData_Sig_Input.PortIndex = 1;
EstimationData_Sig_Input.Name      = 'spe_engine_throttle/Input:1';
EstimationData.InputData = EstimationData_Sig_Input;

Specify the measured output data and associate it with the corresponding model signal.

EstimationData_Sig_Output = Simulink.SimulationData.Signal;
EstimationData_Sig_Output.Values    = timeseries(ThrottlePosition,Time);
EstimationData_Sig_Output.BlockPath = 'spe_engine_throttle/Throttle';
EstimationData_Sig_Output.PortType  = 'outport';
EstimationData_Sig_Output.PortIndex = 1;
EstimationData_Sig_Output.Name      = 'spe_engine_throttle/Throttle:1';
EstimationData.OutputData = EstimationData_Sig_Output;

Add the experiment to the model simulator, so the model simulation uses the information in the experiment.

Simulator = createSimulator(EstimationData,Simulator);

Try the nominal parameter values in the model. To run the model and plot results, use the function spe_engine_throttle_Plots.

spe_engine_throttle_Plots(p,Simulator,EstimationData,Requirements);

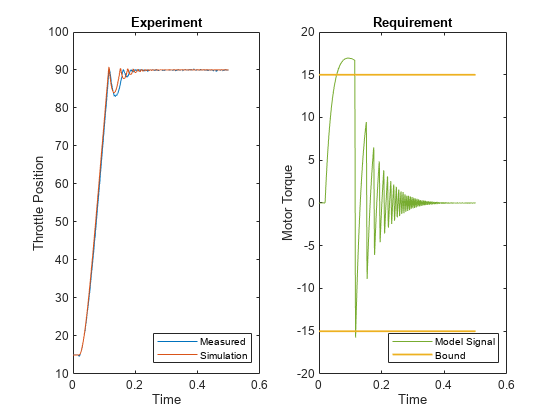
In these plots, the fit between measured data and simulated throttle position is fairly good, but the motor torque does not satisfy the requirement bound, indicating that you can estimate better parameter values.

Optimization Options

To obtain better parameter values, set up parameter estimation. Specify optimization options and use the lsqnonlin optimization solver.

Options = sdo.OptimizeOptions;
Options.Method = 'lsqnonlin';
Options.MethodOptions.ConstraintTolerance = 1e-06;
Options.MethodOptions.FunctionTolerance = 1e-06;
Options.MethodOptions.OptimalityTolerance = 1e-06;
Options.MethodOptions.StepTolerance = 1e-06;
Options.OptimizedModel = Simulator;

Create Estimation Objective Function

Create a function that the optimizer calls at each optimization iteration to compute the estimation cost. Use an anonymous function with one argument that calls spe_engine_throttle_optFcn.

optimfcn = @(P) spe_engine_throttle_optFcn(P,Simulator,EstimationData,Requirements);

Estimate the Parameters

Call sdo.optimize with the estimation objective function handle, parameters to estimate, and options.

[pOpt,Info] = sdo.optimize(optimfcn,p,Options);

 Optimization started 2024-Sep-05, 19:15:02

                                                     First-order 
 Iter F-count        f(x)   constraint    Step-size  optimality
    0     13    0.0574662     0.129775            0
    1     27    0.0543575     0.082508      0.04755         11.1
    2     41     0.100572    0.0183021         0.11         9.41
    3     54     0.139328            0      0.06597         3.08
    4     81     0.139923            0     0.001878       0.0695
    5     94     0.132447            0      0.05279        0.882
    6    107     0.128419            0       0.0452         1.61
    7    120     0.128009            0      0.01623         1.83
    8    133     0.127888            0      0.00945         1.92
    9    146     0.127635            0      0.01431          1.9
   10    159     0.126796            0      0.04807         1.94
   11    173     0.126212            0       0.0539          8.1
   12    186     0.124992            0      0.04926         2.01
   13    199     0.124919            0      0.04806         2.04
   14    212     0.124789            0      0.01381         10.7
   15    225     0.124457            0        0.037         10.7
   16    238     0.124234            0      0.01595         10.7
   17    255     0.124232            0    2.871e-05         7.62
   18    278     0.124217            0    0.0005533         7.62
   19    300     0.124214            0    0.0001202         7.62
   20    322     0.124213            0    2.491e-05         7.62
   21    336     0.124144            0      0.05642         7.45
   22    350     0.123886            0      0.01883         7.36
   23    372     0.123886            0    0.0003386          6.5
   24    389     0.123882            0    0.0004159          6.5
   25    406     0.123828            0     0.004102         1.48
   26    420     0.123795            0     0.005822         1.45
   27    433     0.123184            0      0.09192         1.32
   28    446     0.117404            0       0.7661         1.84
   29    459     0.111045            0        1.053         2.35
   30    472     0.104118            0        1.385            3
   31    485    0.0999091  2.68351e-05        0.936         3.56
   32    498      0.10024            0       0.1103         3.63
   33    511    0.0976555            0       0.6228         4.16
   34    524    0.0947641            0       0.6267         4.74
   35    537    0.0937828            0       0.4654         5.12
   36    550    0.0929246            0       0.3918          5.4
   37    564    0.0925047            0       0.2054         5.13
   38    577    0.0924368            0       0.1594         5.07
   39    590    0.0923055            0       0.1308         4.85
   40    603     0.092266            0      0.08942         4.76
   41    616    0.0922229            0      0.05057          4.7
   42    629    0.0921859            0      0.03367         4.65
   43    642    0.0921624            0      0.03122         4.61
   44    655    0.0921352            0      0.03172         4.55
   45    668    0.0921025            0      0.02115         4.52
   46    681    0.0920949            0     0.009601          4.5
   47    694    0.0920782            0      0.01365         4.47
   48    707    0.0920725            0      0.01738         4.45
   49    721    0.0920384            0      0.01433         4.42

                                                     First-order 
 Iter F-count        f(x)   constraint    Step-size  optimality
   50    737    0.0920352            0     0.004424         4.41
   51    751    0.0920249            0      0.04614         4.26
   52    768    0.0920249            0    1.784e-06      0.00819
Local minimum possible. Constraints satisfied.

lsqnonlin stopped because the size of the current step is less than
the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

The progress display provides information about the iterations from parameter estimation. By the end of the estimation process, the fit between measured data and simulated throttle position is fairly good, as indicated by a small value in the f(x) column. In addition, the requirement is satisfied, as indicated by 0 or a negative value in the constraint column.

Try the optimized parameter values in the model.

spe_engine_throttle_Plots(pOpt,Simulator,EstimationData,Requirements);

The plots show a good fit between measured data and simulated throttle position, and the motor torque satisfies the requirement bound.

Update the experiment with the estimated parameter values.

EstimationData = setEstimatedValues(EstimationData,pOpt);

Update the model with the optimized parameter values.

sdo.setValueInModel('spe_engine_throttle',pOpt);

In summary, the parameters of the engine throttle model are estimated to make the model output match measured data, while also imposing a constraint on the simulated motor torque, to keep it consistent with a known bound.

Close the model.

close_system("spe_engine_throttle");

Example Helper Functions

type spe_engine_throttle_Plots

function spe_engine_throttle_Plots(P,Simulator,EstimationData,Requirements)

%% Evaluate Requirements

% Update parameter values, and simulate the model
Simulator.Parameters = P;
Simulator = sim(Simulator);

% Retrieve logged signal data
SimLog = find(Simulator.LoggedData,get_param('spe_engine_throttle','SignalLoggingName'));
Sig_Log = find(SimLog,'Sig');

%% Evaluate Experiments

% Update parameter values in the experiment, and simulate the model
EstimationData = setEstimatedValues(EstimationData,P);
Simulator = createSimulator(EstimationData,Simulator);
strOT = mat2str(EstimationData.OutputData(1).Values.Time);
Simulator = sim(Simulator, 'OutputOption', 'AdditionalOutputTimes', 'OutputTimes', strOT);

% Retrieve logged signal data
SimLog = find(Simulator.LoggedData,get_param('spe_engine_throttle','SignalLoggingName'));
Sig = find(SimLog,EstimationData.OutputData.Name);

%% Plot Fit to Measured Data in Experiment
colorOrder = colororder('default');
subplot(1,2,1);
plot(EstimationData.OutputData.Values.Time, EstimationData.OutputData.Values.Data, ...
    'Color', colorOrder(1,:), 'DisplayName', 'Measured');
line(Sig.Values.Time, Sig.Values.Data, ...
    'Color', colorOrder(2,:), 'DisplayName', 'Simulation');
legend('Location','southeast');
title('Experiment');
ylabel('Throttle Position');
xlabel('Time');

%% Plot Requirement
subplot(1,2,2);
plot(Sig_Log.Values.Time, Sig_Log.Values.Data, 'Color', colorOrder(5,:));
line(Requirements.SignalBound.BoundTimes, Requirements.SignalBound.BoundMagnitudes, ...
    'Color', colorOrder(3,:), 'LineWidth', 1.25);
if numel(fieldnames(Requirements)) > 1
    line(Requirements.SignalBound2.BoundTimes, Requirements.SignalBound2.BoundMagnitudes, ...
        'Color', colorOrder(3,:), 'LineWidth', 1.25);
end
legend('Model Signal', 'Bound', 'Location','southeast');
title('Requirement');
ylabel('Motor Torque');
xlabel('Time');
end

type spe_engine_throttle_optFcn

function Vals = spe_engine_throttle_optFcn(P,Simulator,EstimationData,Requirements)
%SPE_ENGINE_THROTTLE_OPTFCN
%
% Function called at each iteration of the estimation problem.
%
% The function is called with a set of parameter values, P, and returns
% the estimation cost, Vals, to the optimization solver.
%
% See the sdoExampleCostFunction function and sdo.optimize for a more
% detailed description of the function signature.
%

%% Evaluate Requirements
%
% Simulate the model.
Simulator.Parameters = P;
Simulator = sim(Simulator);

% Retrieve logged signal data.
SimLog = find(Simulator.LoggedData,get_param('spe_engine_throttle','SignalLoggingName'));
Sig_Log = find(SimLog,'Sig');

% Evaluate the design requirements.
Cleq_SignalBound  = evalRequirement(Requirements.SignalBound,  Sig_Log.Values);
Cleq_SignalBound2 = evalRequirement(Requirements.SignalBound2, Sig_Log.Values);


%% Evaluate Experiments
%
% Define a signal tracking requirement to compute how well the model
% output matches the experiment data.
r = sdo.requirements.SignalTracking('Method','Residuals');

%%
% Update the experiment with the estimated parameter values.
EstimationData = setEstimatedValues(EstimationData,P);

%%
% Simulate the model and compare model outputs with measured experiment
% data.

F_r = [];
Simulator = createSimulator(EstimationData,Simulator);
strOT = mat2str(EstimationData.OutputData(1).Values.Time);
Simulator = sim(Simulator, 'OutputOption', 'AdditionalOutputTimes', 'OutputTimes', strOT);

SimLog = find(Simulator.LoggedData,get_param('spe_engine_throttle','SignalLoggingName'));
Sig = find(SimLog,EstimationData.OutputData.Name);

Error = evalRequirement(r,Sig.Values,EstimationData.OutputData.Values);
F_r = [F_r; Error(:)];

%% Return Values.
%
% Return the evaluated estimation cost and requirement values in a
% structure to the optimization solver.
%Return values from cost function
%to optimization solver
Vals.F = F_r;
Vals.Cleq = [...
    Cleq_SignalBound(:) ; ...
    Cleq_SignalBound2(:) ...
    ];
end