Control Design and Disturbance Compensation Using Extended State Observers

Since R2024a

An extended state observer (ESO) is a state estimation technique that allows you to estimate the states and disturbances of a plant based on the its inputs and outputs. The algorithm models disturbances as an extended state of the plant to perform the estimation. This technique is helpful when you want to compensate for unknown disturbances in your control system. These disturbances represent total disturbances, including unknown dynamics and internal and external disturbances.

Extended State Observer Block

You can use the Extended State Observer block to implement ESO in Simulink^®. The block requires you to specify system dynamics in the following form.

$\begin{matrix} \dot{x} / x^{+} = A x + B_{u} u + B_{d} d \\ y_{m} = C_{m} x \end{matrix}$

Here:

x is the plant states
$\dot{x}$ is the state derivative in continuous time and x⁺ is the state update x[k+1] in discrete time.
A, B_u, and C_m are the plant dynamics.
y_m is the measurable plant output.
B_d is the disturbance input matrix. The block allows you to specify the disturbance matrix in the form B_d = k×B_u for matched uncertainties, where k is a gain specified using block parameters. You can also specify B_d as a block input for mismatched uncertainties [1].
d is the total disturbances in the model, including unknown dynamics and internal and external disturbances.

Typically, you obtain these system dynamics from a physical representation or an approximation of the plant. The block does not require you to provide an actual model of the plant. Therefore, the accuracy of estimation will depend on the accuracy of the plant approximation. Based on these plant inputs u and outputs y_m, the block returns estimated the states $\hat{x}$ and disturbances $\hat{d}$ . Using these estimated states and disturbances, you can implement state feedback or disturbance compensation control techniques.

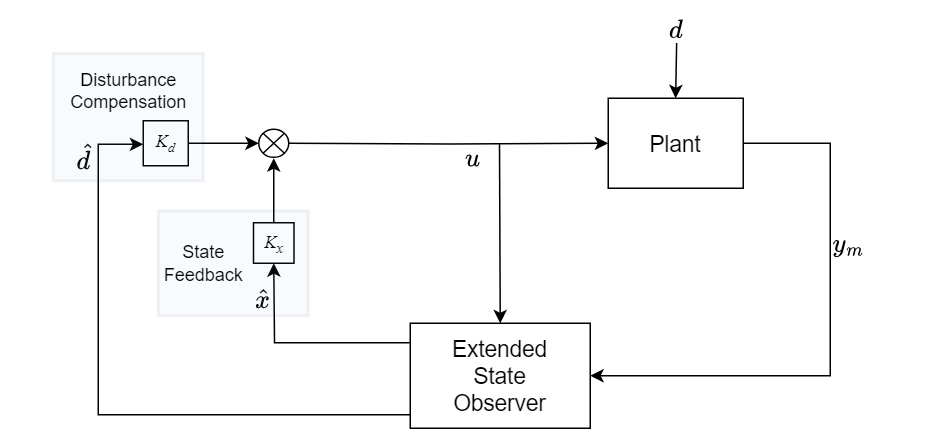
Block diagram of extended state observer

To tune the observer response, use the Bandwidth (rad/s) and Spacing (rad/s) parameters. Using these parameters, the block determines the location and spacing of the poles and calculates the observer gain matrix. You can also specify the observer gain matrix as a block input.

For an example, see Apply Extended State Observer for Reference Tracking of DC Motor.

Disturbance Compensator Block

Use the Disturbance Compensator block to modify control actions of a nominal controller to reject and compensate for disturbances in your model. To compensate for disturbances, the Disturbance Compensator block uses an ESO to estimate total disturbances in the model and returns the modified controller actions you can use as plant input.

The block extends the implementation of ESO described in the previous section as follows.

$\begin{matrix} \dot{x} / x^{+} = A x + B_{u} u + B_{d} d \\ y_{m} = C_{m} x \\ u = u_{0} + K_{d} \hat{d} \end{matrix}$

Here:

u is the modified controller action.
u₀ is the nominal controller action.
K_d is the compensation gain matrix.

A typical structure is shown in this diagram. The highlighted section shows how the Disturbance Compensator block generates the compensation signal.

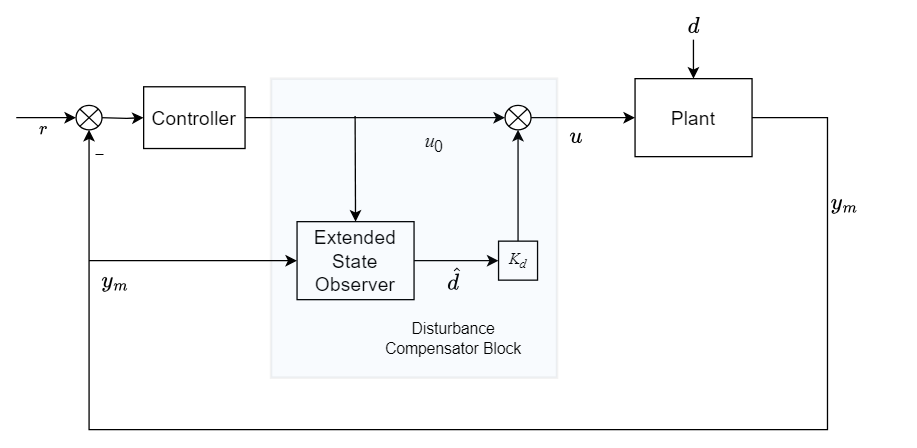
Closed-loop system with disturbance compensator structure.

Similar to the Extended State Observer block, to tune the observer response, use the Bandwidth (rad/s) and Spacing (rad/s) parameters. Using these parameters, the block determines the location and spacing of the poles and calculates the observer gain matrix and the compensation gain matrix K_d. You can also specify the gain matrices as a block inputs.

The calculation of K_d is time-domain dependent. For more information, see [1] and [2].

For an example, see Compensate for Disturbances in Spring-Mass-Damper System.

References

[1] Li, Shihua, Jun Yang, Wen-Hua Chen, and Xisong Chen. “Generalized Extended State Observer Based Control for Systems With Mismatched Uncertainties.” IEEE Transactions on Industrial Electronics 59, no. 12 (December 2012): 4792–4802. https://doi.org/10.1109/TIE.2011.2182011.

[2] Zhang, Pengcheng, Jianyu Wang, Yun Cheng, and Shiyu Jiao. “Reduced-Order Generalized Extended State Observer Based Control for Discrete-Time Systems.” In 2022 International Conference on Cyber-Physical Social Intelligence (ICCSI), 670–75. Nanjing, China: IEEE, 2022. https://doi.org/10.1109/ICCSI55536.2022.9970623.