Choose Step Size and Number of Iterations
The example shows a process to select step size and number of iterations for your real-time model. To optimize your model for simulation on a real-time target machine, specify a combination of step size, Ts, and number of iterations, N, that provides acceptable accuracy and the speed to avoid an overrun. As with solver type, you can specify different combinations of Ts and N values for the Simulink® global solver and for each independent Simscape™ network in your model.
Obtain Reference Results
To obtain reference results, simulate the original version of the hydraulic actuator model.
To open the hydraulic actuator model, at the MATLAB® command prompt, enter:
model = 'ssc_hydraulic_actuator_digital_control'; open_system(model)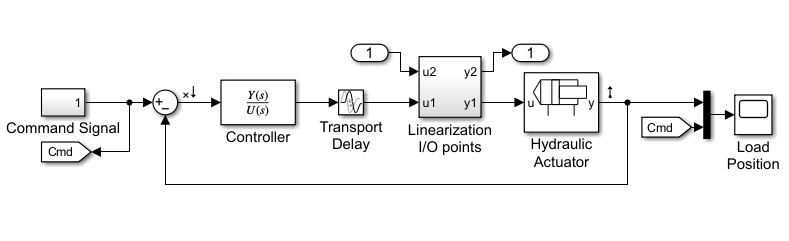
The model is configured to limit data points. To configure the model to log all data points, open the model configuration parameters, and in the Simscape pane, clear the Limit data points check box.
Simulate the model.
sim(model)
Extract the data for pressure and simulation-step time from the logged Simscape node.
simlogRef = simlog_ssc_hydraulic_actuator_digital_control; pRefNode = simlogRef.Hydraulic_Actuator.Hydraulic_Cylinder.Chamber_A.A.p; pRef = pRefNode.series.values('Pa'); tRef = pRefNode.series.time;Plot the step size.
h1 = figure; semilogy(tRef(1:end-1),diff(tRef),'-x') title('Solver Step Size') xlabel('Time (s)') ylabel('Step Size (s)')

The maximum step size (Tsmax) for obtaining accurate real-time results for the original model is approximately 1e-2 seconds. For information on determining Tsmax, see Determine Step Size.
Plot the simulation results.
h2 = figure; plot(tRef,pRef, 'b-') h2Legend1 = legend({'Reference'},'Location','southoutside'); title('Cylinder Pressure') xlabel('Time (s)') ylabel('Pressure (Pa)')

Determine Maximum Step Size for Accurate Results
In a modified version of the hydraulic actuator model, you can change the value of Tsmax, the maximum step size for achieving accurate real-time simulation results.
Open the modified hydraulic actuator model.
ssc_hydraulic_actuator_HIL

This version of the hydraulic actuator contains a discretized, partitioned controller. The local solver for the hydraulic actuator subsystem is enabled for fixed-step, fixed-cost simulation. The step size is parameterized (ts) so that you can make solver adjustments that decrease the likelihood of generating an overrun. For an example that shows how to discretize the controller for the hydraulic actuator, see Hydraulic Actuator Configured for HIL Testing.
To determine the maximum step size to use for achieving accurate real-time simulation results, you simulate with a global, variable-step solver. To configure the modified model for variable-step simulation using the global solver, disable the local solver configuration. In the Hydraulic Actuator subsystem, in the Solver Configuration block property inspector, clear the Use local solver check box.
Simulate the model.
Extract the data for pressure and time from the logged Simscape node.
simlog0 = simlog_ssc_hydraulic_actuator_HIL; pNodeSim0 = simlog0.Hydraulic_Actuator.Hydraulic_Cylinder.Chamber_A.A.p; pSim0 = pNodeSim0.series.values('Pa'); tSim0 = pNodeSim0.series.time;Plot the step size to the figure that contains the step-size data for the original model.
figure(h1) hold on semilogy(tSim0(1:end-1),diff(tSim0),'--x', 'Color','r',... 'LineWidth',.1,'MarkerSize',5) title('Solver Step Size') xlabel('Time (s)') ylabel('Step Size (s)') h1Legend1 = legend({'Reference','Modified'},... 'Location','southoutside');

For the discretized model, Tsmax is between 1e-2 and 1e-3 seconds.
Parameterize Global and Local Solver Settings
To reduce the number of steps for finding the optimal real-time-simulation solver settings, parameterize the solver configuration with workspace variables. In the Hydraulic Actuator Discrete Model, the step size for the local solver configuration is specified as the workspace variable ts. For this example, you also use workspace variables to parameterize the global step size (tsG) and the local number of nonlinear iterations (N).
For the modified model, in the model configuration parameters property inspector, specify these settings:
Pane Parameter Value Purpose Solver
Type Fixed-stepConfigure the global solver of the modified model for fixed-step simulation. Solver discrete (no continuous states)Configure the global solver to match the state of the controller. Additional options> Fixed-step size (fundamental sample time)tsGParameterize the global step size. Simscape
Limit data points Clear the check box. As you decrease the solver step size, the number of data points that the simulation generates increases. Clear the option to ensure that you collect all the data that you need for evaluating simulation accuracy. Configure the local solver for fixed-step simulation. In the Hydraulic Actuator subsystem, in the Solver Configuration block property inspector, select Use local solver.
To parameterize the cost of the simulation, set Nonlinear iterations to
N.
Perform Fixed-Step, Fixed-Cost Simulation
You can determine if your solver settings are appropriate for real-time simulation by simulating the model and then evaluating the accuracy of the results and the speed of the simulation. To evaluate accuracy, compare the results to the reference results and to the results of other fixed-step, fixed-cost simulations. To evaluate simulation speed, compare the elapsed time to the specified simulation time and to the simulation execution budget. If the speed or accuracy is not acceptable, adjust the step size and number of iterations to make your model real-time capable.
The simulation execution-time budget for this example is four seconds. For information on determining the execution-time budget for your model, see Estimate Computation Costs.
For the first simulation, specify both the global and local step size as the largest possible value of Tsmax from the step plot. Specify a relatively large value for the step size for both solvers and three for the number of nonlinear iterations for the local solver.
ts = 1e-2; tsG = 1e-2; N = 3;
Perform a timed fixed-step, fixed-cost simulation.
tic; sim('ssc_hydraulic_actuator_HIL'); tSim1 = toc; time1 = max(tSim1);Extract the data for pressure and simulation time from the logged Simscape node.
simlog1 = simlog_ssc_hydraulic_actuator_HIL; pNodeSim1 = simlog1.Hydraulic_Actuator.Hydraulic_Cylinder.Chamber_A.A.p; pSim1 = pNodeSim1.series.values('Pa'); tSim1 = pNodeSim1.series.time;Plot the simulation results to the figure that contains the reference results. Write the elapsed time to the figure legend.
figure(h2) hold on plot(tSim1, pSim1, 'g--') delete(h2Legend1) configSim1L = ['Local: Ts= ',num2str(ts),'s, N= ',num2str(N),'.']; configSim1G = [' Global: Ts= ',num2str(tsG),'s.']; timeSim1T = ['Time=',num2str(time1)]; cfgSim1 = [configSim1L,configSim1G,timeSim1T]; h2Legend2 = legend({'Reference',num2str(cfgSim1)},... 'Location','southoutside');

The elapsed time varies because it depends on the immediate computational capacity of the computer that runs the simulation. The elapsed times in the legend are from simulation on a 3.6-GHz Intel® CPU with a 16-GB memory. Your legend contains the elapsed time for the simulation on your computer.
The simulation took less time to complete than the specified simulation time (10 s) so it runs faster than real time on the development computer. The elapsed time is also less than the simulation execution-time budget for this example (four seconds). Therefore, the specified solver configuration provides an acceptable safety margin for real-time simulation on the target machine that provided the budget data.
Zoom to an inflection point to evaluate the accuracy of the results.
figure(h2) xStart = 0; xEnd = 10; yStart = 0; yEnd = 3.5e6; xZoomStart = 0.3; xZoomEnd = 0.6; yZoomStart = 2.6e6; yZoomEnd = 3.5e6; axis([xZoomStart xZoomEnd yZoomStart yZoomEnd])

Theoretical and empirical data support the reference results. The accuracy of the simulation results is not acceptable because the solver oscillates before it converges on the solution in the reference data.
If you can achieve acceptable result accuracy, but the simulation runs too slowly for a given execution-time budget, increase speed by increasing the step size or decrease the number of iterations.
When you find a combination of solver settings that provide accurate enough results and a simulation speed that fits your execution-time budget, you can attempt to run your model on a real-time target machine by performing the hardware-in-the-loop simulation workflow. If you cannot find the right combination of solver settings, perform the real-time model preparation workflow or increase your real-time computing capability to improve simulation speed and accuracy. To increase your real-time computing capability, upgrade your target hardware or partition your model for parallel processing.
Adjust Solver Settings to Improve Accuracy
You can generally improve accuracy by increasing the number of iterations or by decreasing the step size.
Try to improve accuracy by increasing the number of iterations (N) to 10.
N = 10;
Run a timed simulation.
tic; sim('ssc_hydraulic_actuator_HIL'); tSim2 = toc; time2 = max(tSim2);Extract the pressure and simulation time data.
simlog2 = simlog_ssc_hydraulic_actuator_HIL; pNodeSim2 = simlog2.Hydraulic_Actuator.Hydraulic_Cylinder.Chamber_A.A.p; pSim2 = pNodeSim2.series.values('Pa'); tSim2 = pNodeSim2.series.time;Plot the results.
figure(h2) hold on plot(tSim2, pSim2, 'r:') delete(h2Legend2) axis([xStart xEnd yStart yEnd]) configSim2L = ['Local: Ts= ',num2str(ts),'s, N= ',num2str(N),'.']; configSim2G = [' Global: Ts= ',num2str(tsG),'s.']; timeSim2T = ['Time=',num2str(time2)]; cfgSim2 = [configSim2L,configSim2G,timeSim2T]; h2Legend3 = legend({'Reference',num2str(cfgSim1),num2str(cfgSim2)},... 'Location','southoutside');

The simulation is fast enough for real-time simulation because it took less time to run than the four-second simulation execution budget.
Zoom to evaluate accuracy.
figure(h2) axis([xZoomStart xZoomEnd yZoomStart yZoomEnd])

Overall, the results are not much more accurate than the results from the simulation with fewer iterations.
Try to improve accuracy by decreasing the step size to 1e-3 seconds for the local and global solvers. Specify
3for the number of iterations (N).ts = 1e-3; tsG = 1e-3; N = 3;
Run a timed simulation.
tic; sim('ssc_hydraulic_actuator_HIL'); tSim3 = toc; time3 = max(tSim3);Extract the pressure and simulation time data.
simlog3 = simlog_ssc_hydraulic_actuator_HIL; pNodeSim3 = simlog3.Hydraulic_Actuator.Hydraulic_Cylinder.Chamber_A.A.p; pSim3 = pNodeSim3.series.values('Pa'); tSim3 = pNodeSim3.series.time;Plot the results.
figure(h2) hold on plot(tSim3, pSim3, 'k--') delete(h2Legend3) axis([xStart xEnd yStart yEnd]) configSim3L = ['Local: Ts= ',num2str(ts),'s, N= ',num2str(N),'.']; configSim3G = [' Global: Ts= ',num2str(tsG),'s.']; timeSim3T = ['Time=',num2str(time3)]; cfgSim3 = [configSim3L,configSim3G,timeSim3T]; h2Legend4 = legend... ({'Reference',num2str(cfgSim1),num2str(cfgSim2),num2str(cfgSim3)},... 'Location','southoutside');

The simulation takes longer but is fast enough given the four-second simulation execution-time budget.
Zoom to evaluate accuracy better.
figure(h2) axis([xZoomStart xZoomEnd yZoomStart yZoomEnd])

The accuracy of the results is acceptable. For real-time simulation with the modified model, use the solver settings that provided acceptable speed and accuracy:
Three nonlinear iterations
Global and local step sizes of 1e-3 seconds
If you can achieve accurate enough results, but the simulation runs too slowly for your execution-time budget, improve speed by increasing the step size or decreasing the number of iterations.
When you find a combination of solver settings that provides accurate enough results and a simulation speed that is less than your execution-time budget, you can run your model on a real-time target machine. To run your model on a real-time target machine, perform the hardware-in-the-loop simulation workflow.
If you cannot find the right combination of solver settings for real-time simulation, improve simulation speed and accuracy by modifying the scope or fidelity of your model. For more information, see Model Preparation Process.
If you cannot make your model real-time capable by changing the scope or fidelity of your model, increase your real-time computing capability. For more information, see Simulating Parts of the System in Parallel.
See Also
Solver Profiler | simscape.getLocalSolverFixedCostInfo
Topics
- Determine Step Size
- Determine System Stiffness
- Estimate Computation Costs
- Filtering Input Signals and Providing Time Derivatives
- Fixed-Cost Simulation for Real-Time Viability
- Real-Time Code Generation and Deployment Process
- Improving Speed and Accuracy
- Log and Plot Simulation Data
- Model Preparation Process
- Solvers for Real-Time Simulation
- Basics of Hardware-in-the-Loop Simulation