Model Noise in an RF System
The RF Blockset™ Equivalent Baseband Physical library blocks can model noise. The Input Port block parameters specify whether to include noise in a simulation. When you include noise information in your model, the blockset simulates the noise of the physical system by combining the noise contributions from each individual block. This section explains how the blockset simulates noise from user-specified information. For information on how to add noise to an RF model, see Model Noise.
Output-Referred Noise in RF Models
In general, you can specify output-referred noise in one of three ways:
Noise temperature— Specifies the noise in kelvin.Noise factor— Specifies the noise by the following equation:Noise figure— Specifies the noise in decibels relative to the standard reference noise temperature of 290 K. In terms of noise factorNoise figure = 10log(Noise factor)
These three specifications are equivalent, because you can compute each one from any of the others.
The blockset lets you simulate the noise associated with any physical block in your RF model.
The blockset automatically determines the noise properties of passive blocks from their network parameters. The blockset gets these network parameters either explicitly from the block dialog box or specified data files, or implicitly by calculating them from the specified block parameters.
For active devices such as amplifiers and mixers, the noise properties cannot be inferred from network parameters. Therefore, for the amplifier and mixer blocks, you must specify the noise information explicitly, either in the dialog block or the associated data file.
For physical amplifier and mixer blocks, you can specify active block noise in one of the following ways:
Spot noise data
Frequency-independent noise figure, noise factor, or noise temperature values
Frequency-dependent noise figure data (
rfdata.nf) or spot noise data (rfdata.noise) object
These noise specification options are described in Amplifier and Mixer Noise Specifications.
When you run the simulation, the blockset first computes the noise figure values for each individual block at the modeling frequencies. Then, it computes the noise figure of the physical system from the individual noise figure values and uses the system noise figure information to calculate the output noise power. This process is shown in the following figure.
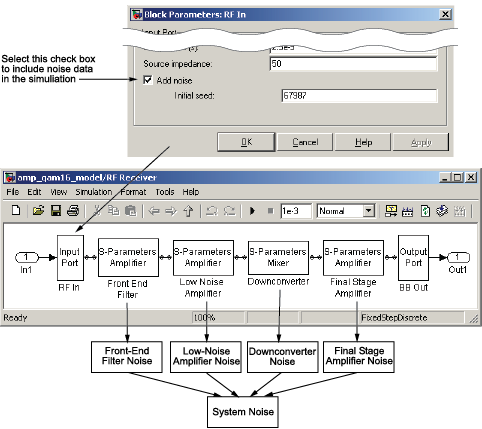
Calculate Noise Figure at Modeling Frequencies
To include noise information in a simulation, the blockset must compute the noise figure values of each individual block at the modeling frequencies.
If you specify the frequency-independent noise figure value directly, or if the blockset computes the noise figure value from the block resistance, the blockset uses this value for the noise figure value at each of the modeling frequencies.
If you specify the noise factor or noise temperature value, the blockset computes the noise figure value from the specified value using the equations in the preceding section and uses the computed value for the noise figure value at each of the modeling frequencies.
If you specify frequency-dependent noise figure values using
an rfdata.nf object, the blockset interpolates
the values using the Interpolation method specified
in the block dialog box to get the noise figure value at each of the
modeling frequencies.
If you specify spot noise data, the blockset computes frequency-dependent noise figure information from this data. It takes the minimum noise figure, NFmin, equivalent noise resistance, Rn, and optimal source admittance, Yopt, values in the file and interpolates to find the values at the modeling frequencies. Then, the blockset uses the following equation to calculate the noise correlation matrix, CA:
where k is Boltzmann's constant, and T is the noise temperature in Kelvin.
The blockset then calculates the noise factor, F, from the noise correlation matrix as follows:
In the two preceding equations, ZS is the nominal impedance, which is 50 ohms, and z+ is the Hermitian conjugation of z.
The blockset obtains the noise figure, NF, from the noise factor:
Calculate System Noise Figure
The blockset uses a recursive process to calculate system noise figure. The noise correlation matrices for the first two elements of the cascade are combined into a single matrix, and the process is repeated.
The following figure shows a cascaded network consisting of two 2-port networks, each represented by its ABCD-parameters.

First, the blockset calculates noise correlation matrices CA' and CA” for the two networks. Then, the blockset combines CA′ and CA″ into a single correlation matrix CA using the equation
The ABCD-parameter matrices in the cascade combine according to matrix multiplication:
If there is another element in the cascade, the same calculations will be performed using these ABCD-parameters as well as the ABCD-parameters corresponding to the following element. The recursion will terminate with a noise correlation matrix pertaining to the entire system. The blockset then calculates the system noise figure from this matrix.
For more information about these calculation techniques, see the following article:
Hillbrand, H. and P.H. Russer, “An Efficient Method for Computer Aided Noise Analysis of Linear Amplifier Networks,” IEEE Transactions on Circuits and Systems, Vol. CAS-23, Number 4, pp. 235–238, 1976.
Calculate Output Noise Power
The blockset uses noise power to determine the amplitude of the noise that it adds to the physical system using a Gaussian distributed pseudorandom number generator. It uses both the noise temperature and the modeling bandwidth to calculate the noise power:
Noise power = kTB
The blockset computes noise temperature from the specified or calculated noise figure values for the system, and it computes the modeling bandwidth from the model's sample time and center frequency.