Human Health Monitoring Using Continuous Wave Radar and Deep Learning
This example shows how to reconstruct electrocardiogram (ECG) signals via continuous wave (CW) radar signals using deep learning neural networks.
Radar is now being used for vital sign monitoring. This method offers many advantages over wearable devices. It allows non-contact measurement which is preferred for use in cases of daily use of long-term monitoring. However, the challenge is that we need to convert radar signals to vital signs or to meaningful biosignals that can be interpreted by physicians. Current traditional methods based on signal transform and correlation analysis can capture periodic heartbeats but fail to reconstruct the ECG signal from the radar returns. This example shows how AI, specifically a deep learning network, can be used to reconstruct ECG signals solely from the radar measurements.
This example uses a hybrid convolutional autoencoder and bidirectional long short-term memory (BiLSTM) network as the model. Then, a wavelet multiresolution decomposition layer, maximal overlap discrete wavelet transform (MODWT) layer, is introduced to improve the performance. The example compares the network using a 1-D convolutional layer and network using a MODWT layer.
Data Description
The dataset [1] presented in this example consists of synchronized data from a CW radar and ECG signals measured simultaneously by a reference device on 30 healthy subjects. The implemented CW radar system is based on the Six-Port technology and operates at 24 GHz in the Industrial Scientific and Medical (ISM) band.
Due to the large volume of the original dataset, for efficiency of model training, only a small subset of the data is used in this example. Specifically, the data from three scenarios, resting, apnea, and Valsalva maneuver, is selected. Further, the data from subjects 1-5 is used to train and validate the model. The data from subject 6 is used to test the trained model.
Also, because the main information contained in the ECG signal is usually located in a frequency band less than 100 Hz, all signals are downsampled to 200 Hz and divided into segments of 1024 points, i.e. signals of approximately 5s.
Download and Prepare Data
The data has been uploaded to this location: https://ssd.mathworks.com/supportfiles/SPT/data/SynchronizedRadarECGData.zip.
Download the dataset using the downloadSupportFile function. The whole dataset is approximately 16 MB in size. It contains two folders, trainVal for training and validation data and test for test data. Inside each of them, ECG signals and radar signals are stored in two separate folders, ecg and radar.
datasetZipFile = matlab.internal.examples.downloadSupportFile('SPT','data/SynchronizedRadarECGData.zip'); datasetFolder = fullfile(fileparts(datasetZipFile),'SynchronizedRadarECGData'); if ~exist(datasetFolder,'dir') unzip(datasetZipFile,datasetFolder); end
Create signal datastores to access the data in the files.
radarTrainValDs = signalDatastore(fullfile(datasetFolder,"trainVal","radar")); radarTestDs = signalDatastore(fullfile(datasetFolder,"test","radar")); ecgTrainValDs = signalDatastore(fullfile(datasetFolder,"trainVal","ecg")); ecgTestDs = signalDatastore(fullfile(datasetFolder,"test","ecg"));
View the categories and distribution of the data contained in the training and test sets. Note the GDN000X represents measurement data from subject X and not every subject has data for all three scenarios.
trainCats = filenames2labels(radarTrainValDs,'ExtractBefore','_radar'); summary(trainCats)
GDN0001_Resting 59
GDN0001_Valsalva 97
GDN0002_Resting 60
GDN0002_Valsalva 97
GDN0003_Resting 58
GDN0003_Valsalva 103
GDN0004_Apnea 14
GDN0004_Resting 58
GDN0004_Valsalva 106
GDN0005_Apnea 14
GDN0005_Resting 59
GDN0005_Valsalva 105
testCats = filenames2labels(radarTestDs,'ExtractBefore','_radar'); summary(testCats)
GDN0006_Apnea 14
GDN0006_Resting 59
GDN0006_Valsalva 127
Apply normalization on ECG signals. Center each signal by subtracting its median and rescale it so that its maximum peak is 1.
ecgTrainValDs = transform(ecgTrainValDs,@helperNormalize); ecgTestDs = transform(ecgTestDs,@helperNormalize);
Combine radar and ECG signal datastores. Then, further split the training and validation dataset. Use 90% of data for training and 10% for validation. Set the random seed so that data segmentation and visualization results are reproducible.
trainValDs = combine(radarTrainValDs,ecgTrainValDs);
testDs = combine(radarTestDs,ecgTestDs);
rng("default")
splitIndices = splitlabels(trainCats,0.85);
numTrain = length(splitIndices{1})numTrain = 704
numVal = length(splitIndices{2})numVal = 126
numTest = length(testCats)
numTest = 200
trainDs = subset(trainValDs,splitIndices{1});
valDs = subset(trainValDs,splitIndices{2});Because the dataset used here is not large, read the training, testing, and validation data into memory.
trainData = readall(trainDs); valData = readall(valDs); testData = readall(testDs);
Preview Data
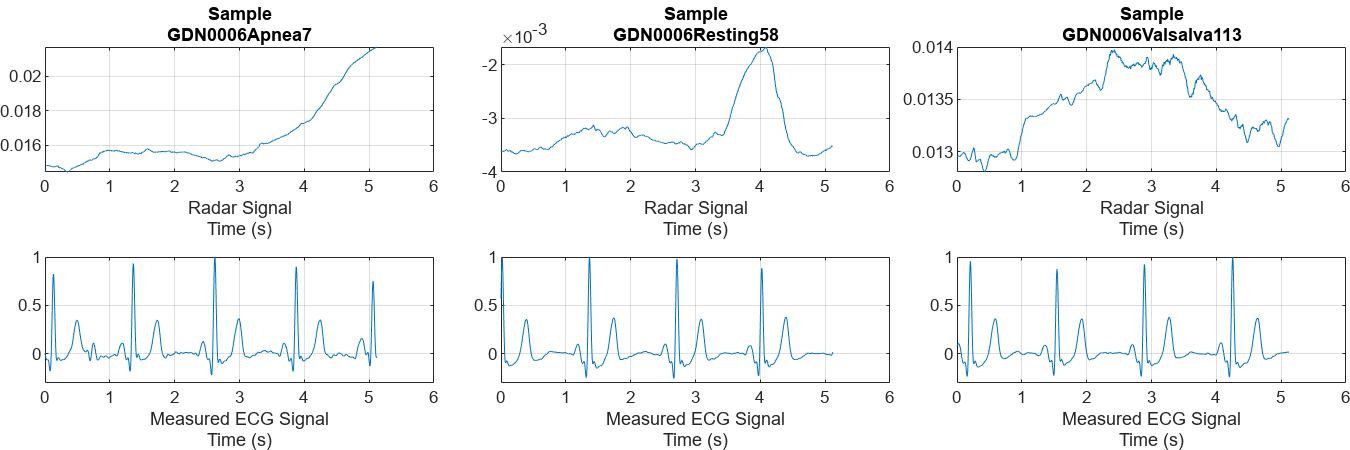
Plot a representative of each type of signal. Notice that it is almost impossible to identify any correlation between the radar signals and the corresponding reference ECG measurements.
numCats = cumsum(countcats(testCats)); previewindices = [randi([1,numCats(1)]),randi([numCats(1)+1,numCats(2)]),randi([numCats(2)+1,numCats(3)])]; testindices = [randi([1,numCats(1)]),randi([numCats(1)+1,numCats(2)]),randi([numCats(2)+1,numCats(3)])]; helperPlotData(testDs,previewindices);
Train Convolutional Autoencoder and BiLSTM Model
Build a hybrid convolutional autoencoder and BiLSTM network to reconstruct ECG signals. The first 1-D convolutional layer filters the signal. Then, the convolutional autoencoder eliminates most of the high-frequency noise and captures the high-level patterns of the whole signal. The subsequent BiLSTM layer further finely shapes the signal details.
layers1 = [
sequenceInputLayer(1,MinLength = 1024)
convolution1dLayer(4,3,Padding="same")
layerNormalizationLayer()
dropoutLayer(0.2)
convolution1dLayer(64,8,Padding="same",Stride=8)
reluLayer
batchNormalizationLayer
dropoutLayer(0.2)
maxPooling1dLayer(2,Padding="same")
convolution1dLayer(32,8,Padding="same",Stride=4)
reluLayer
batchNormalizationLayer
maxPooling1dLayer(2,Padding="same")
transposedConv1dLayer(32,8,Cropping="same",Stride=4)
reluLayer
transposedConv1dLayer(64,8,Cropping="same",Stride=8)
bilstmLayer(8)
fullyConnectedLayer(4)
fullyConnectedLayer(2)
fullyConnectedLayer(1)
];Define the training option parameters: use an Adam optimizer and choose to shuffle the data at every epoch. Also, specify radarVal and ecgVal as the source for the validation data. Use the trainnet function to train the model. At the same time, the training information is recorded, which will be used for performance analysis and comparison later.
Train on a GPU if one is available. Using a GPU requires Parallel Computing Toolbox™ and a supported GPU device. For information on supported devices, see GPU Computing Requirements (Parallel Computing Toolbox) (Parallel Computing Toolbox).
options = trainingOptions("adam",... MaxEpochs=800,... MiniBatchSize=900,... InitialLearnRate=0.001,... ValidationData={valData(:,1),valData(:,2)},... ValidationFrequency=40,... VerboseFrequency=40,... Verbose=1, ... Shuffle="every-epoch",... OutputNetwork="best-validation", ... Plots="none", ... InputDataFormats="CTB", ... TargetDataFormats="CTB"); lossFcn = @(y,t)sum(mse(y,t),3); [net1,info1] = trainnet(trainData(:,1),trainData(:,2),layers1,lossFcn,options);
Iteration Epoch TimeElapsed LearnRate TrainingLoss ValidationLoss
_________ _____ ___________ _________ ____________ ______________
0 0 00:00:10 0.001 18.144
1 1 00:00:12 0.001 18.339
40 40 00:00:40 0.001 16.962 16.836
80 80 00:00:57 0.001 16.955 16.868
120 120 00:01:14 0.001 16.951 16.861
160 160 00:01:36 0.001 16.95 16.864
200 200 00:01:58 0.001 16.946 16.88
240 240 00:02:17 0.001 16.942 16.908
280 280 00:02:35 0.001 16.932 16.882
320 320 00:02:50 0.001 16.908 16.89
360 360 00:03:10 0.001 16.828 16.751
400 400 00:03:25 0.001 16.718 16.86
440 440 00:03:40 0.001 16.916 16.814
480 480 00:03:57 0.001 16.888 16.783
520 520 00:04:21 0.001 16.872 16.747
560 560 00:04:35 0.001 16.764 16.62
600 600 00:04:50 0.001 16.496 16.222
640 640 00:05:05 0.001 16.349 15.959
680 680 00:05:19 0.001 16.334 15.9
720 720 00:05:35 0.001 16.22 15.912
760 760 00:05:50 0.001 16.237 15.921
800 800 00:06:05 0.001 16.174 15.768
Training stopped: Max epochs completed
Analyze Performance of Trained Model
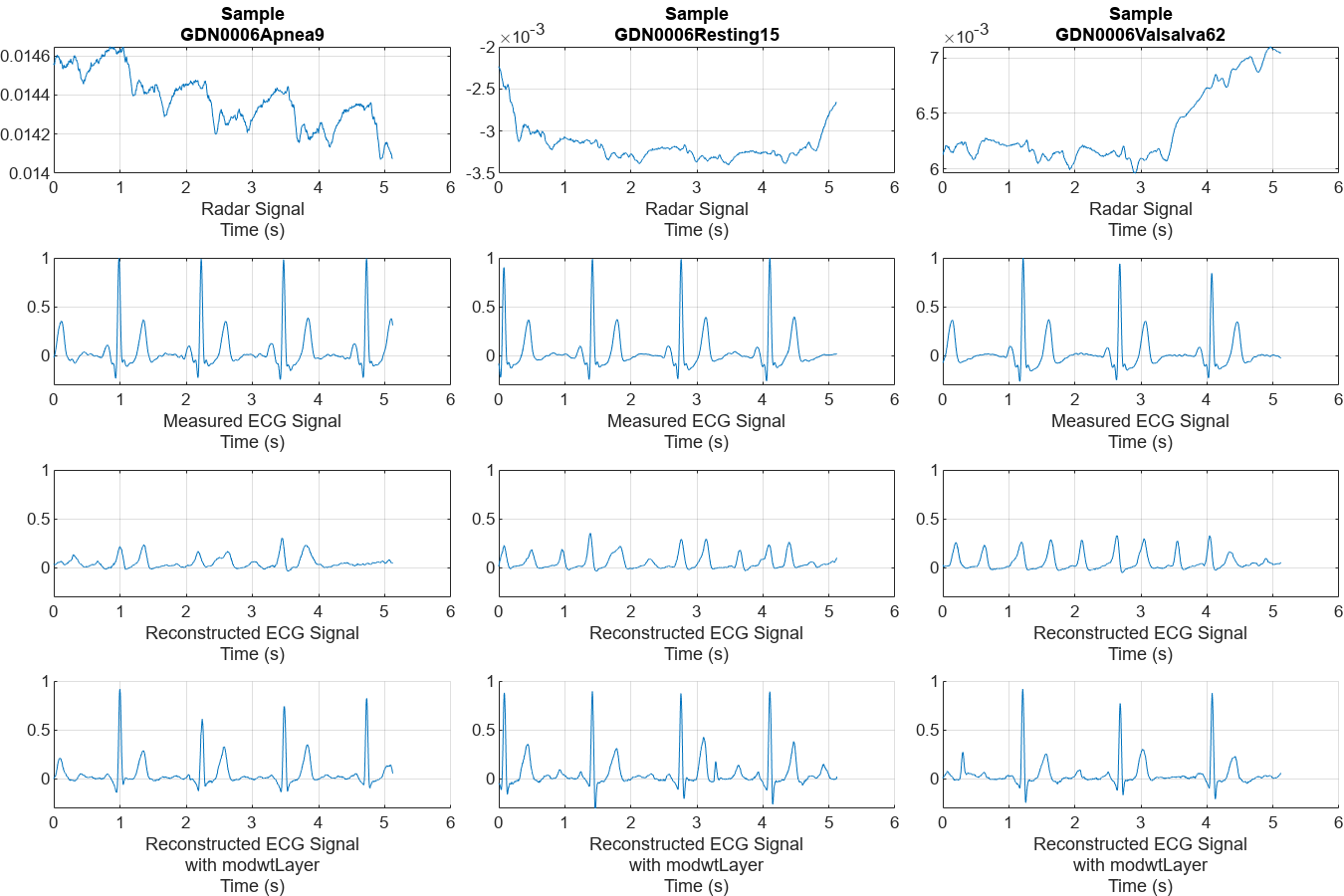
Randomly pick a representative sample of each type from the test dataset to visualize and get an initial intuition about the accuracy of the reconstructions of the trained model.
helperPlotData(testDs,testindices,net1);
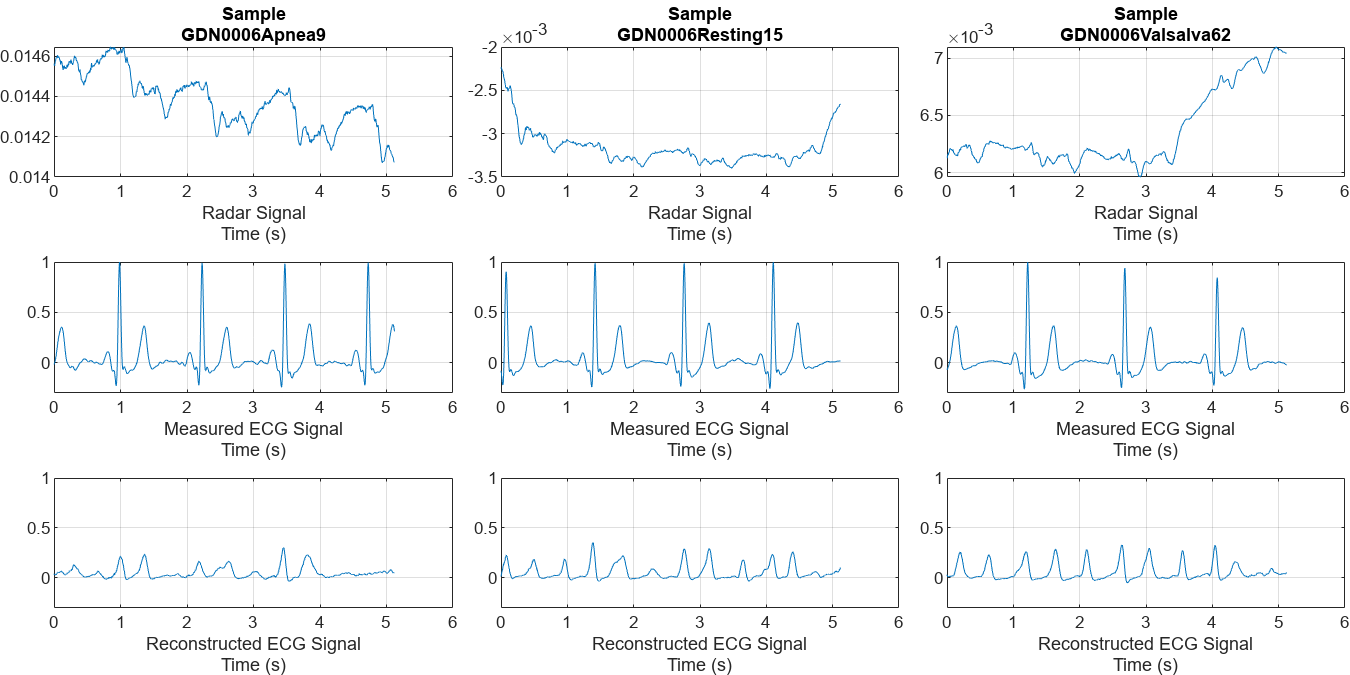
Comparing the measured and reconstructed ECG signals, it can be seen that the model has been able to initially learn some correlations between the radar and ECG signals. But the results are not very satisfactory. Some peaks are not aligned with the actual peaks and the waveform shapes do not resemble those of the measured ECG. A few peaks are even completely lost.
Improve Performance Using Multiresolution Analysis and MODWT Layer
Feature extraction is often used to capture the key information of the signals, reduce the dimensionality and redundancy of the data, and help the model achieve better results. Considering that the effective information of the ECG signal exists in a certain frequency range. Use MODWT to decompose the radar signals and get the multiresolution analysis (MRA) of it as the feature.
It can be found that some components of the radar signal decomposed by MODWTMRA, such as the component of level 4, have similar periodic patterns with the measured ECG signal. Meanwhile, some components contain almost complete noise. Inspired by this, introducing MODWT layer into the model and selecting only a few level components may help the network focus more on correlated information, while also reducing irrelevant interference.
ds = subset(trainDs,1);
[~,name,~] = fileparts(ds.UnderlyingDatastores{1}.Files{1});
data = read(ds);
radar = data{1};
ecg = data{2};
levs = 1:6;
idx = 100:800;
m = modwt(radar,'sym4',max(levs));
nplot = length(levs)+2;
mra = modwtmra(m);
figure
tiledlayout(nplot,1)
nexttile
plot(ecg(idx))
title(["ECG Signal and Radar Signal MODWTMRA", "of Sample " + regexprep(name, {'_','radar'}, '')])
ylabel("Measured ECG")
grid on
d = 1;
for i = levs
d = d+1;
nexttile
plot(mra(i,idx))
ylabel(["Radar", "MODWTMRA", "Level " + i'])
grid on
end
nexttile
plot(mra(i+1,idx))
ylabel(["Radar", "MODWTMRA","Scaling","Coefficients"])
grid on
set(gcf,'Position',[0 0 700,800])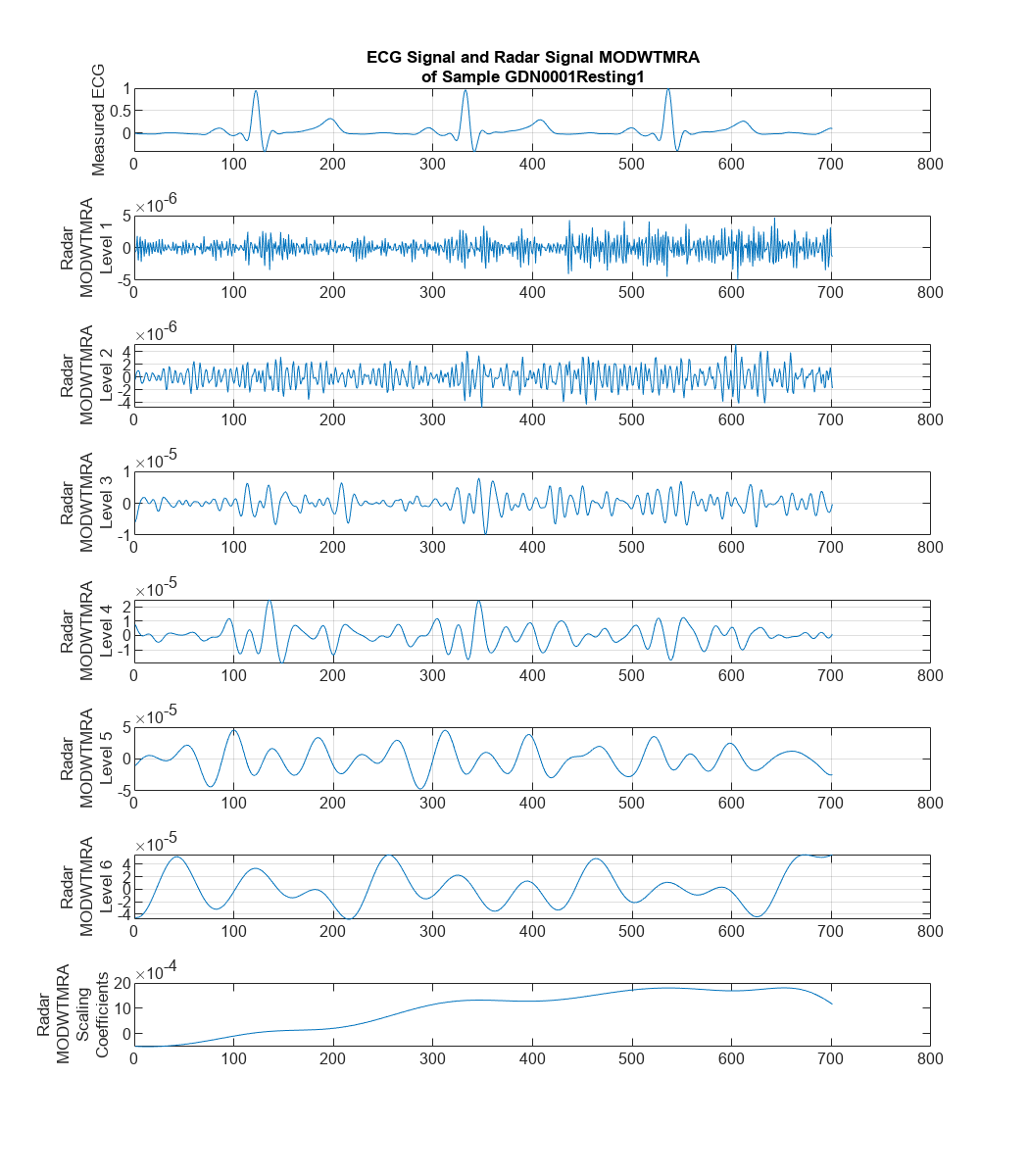
Replace the first convolution1dLayer with modwtLayer. The MODWT layer has been configured to have the same filter size and number of output channels to preserve the number of learning parameters. Based on the observations before, only components of a specific frequency range are preserved, i.e. level 3 to 5, which effectively removes unnecessary signal information that is irrelevant to the ECG reconstruction. Refer to modwtLayer (Wavelet Toolbox) documentation for more details on modwtLayer and these parameters.
A flattenLayer is also inserted after the modwtLayer to make the subsequent convolution1dLayer convolve along the time dimension, and to make the output format compatible with the subsequent bilstmLayer.
layers2 = [
sequenceInputLayer(1,MinLength = 1024)
modwtLayer('Level',5,'IncludeLowpass',false,'SelectedLevels',3:5,"Wavelet","sym4")
flattenLayer
layerNormalizationLayer()
dropoutLayer(0.2)
convolution1dLayer(64,8,Padding="same",Stride=8)
reluLayer
batchNormalizationLayer
dropoutLayer(0.2)
maxPooling1dLayer(2,Padding="same")
convolution1dLayer(32,8,Padding="same",Stride=4)
reluLayer
batchNormalizationLayer
maxPooling1dLayer(2,Padding="same")
transposedConv1dLayer(32,8,Cropping="same",Stride=4)
reluLayer
transposedConv1dLayer(64,8,Cropping="same",Stride=8)
bilstmLayer(8)
fullyConnectedLayer(4)
fullyConnectedLayer(2)
fullyConnectedLayer(1)
];Use the same training options as before.
options = trainingOptions("adam",... MaxEpochs=800,... MiniBatchSize=900,... InitialLearnRate=0.001,... ValidationData={valData(:,1),valData(:,2)},... ValidationFrequency=40,... VerboseFrequency=40,... Verbose=1, ... Shuffle="every-epoch",... OutputNetwork="best-validation", ... Plots="none", ... InputDataFormats="CTB", ... TargetDataFormats="CTB"); lossFcn = @(y,t)sum(mse(y,t),3); [net2,info2] = trainnet(trainData(:,1),trainData(:,2),layers2,lossFcn,options);
Iteration Epoch TimeElapsed LearnRate TrainingLoss ValidationLoss
_________ _____ ___________ _________ ____________ ______________
0 0 00:00:08 0.001 18.136
1 1 00:00:09 0.001 19.273
40 40 00:00:36 0.001 16.703 16.764
80 80 00:01:00 0.001 14.321 14.273
120 120 00:01:23 0.001 11.335 10.619
160 160 00:01:45 0.001 9.5305 8.3391
200 200 00:02:14 0.001 8.5322 7.6323
240 240 00:02:46 0.001 7.911 7.2792
280 280 00:03:09 0.001 7.5802 7.0774
320 320 00:03:30 0.001 7.3912 6.9763
360 360 00:03:53 0.001 7.1857 6.8751
400 400 00:04:14 0.001 6.9099 6.7819
440 440 00:04:35 0.001 6.7748 6.9208
480 480 00:04:55 0.001 6.6766 6.8344
520 520 00:05:25 0.001 6.4978 6.6761
560 560 00:05:46 0.001 6.442 6.734
600 600 00:06:06 0.001 6.3567 6.7029
640 640 00:06:26 0.001 6.2753 6.7114
680 680 00:06:47 0.001 6.2243 6.7499
720 720 00:07:08 0.001 6.0981 6.6829
760 760 00:07:29 0.001 5.999 6.6683
800 800 00:07:50 0.001 6.0931 6.6166
Training stopped: Max epochs completed
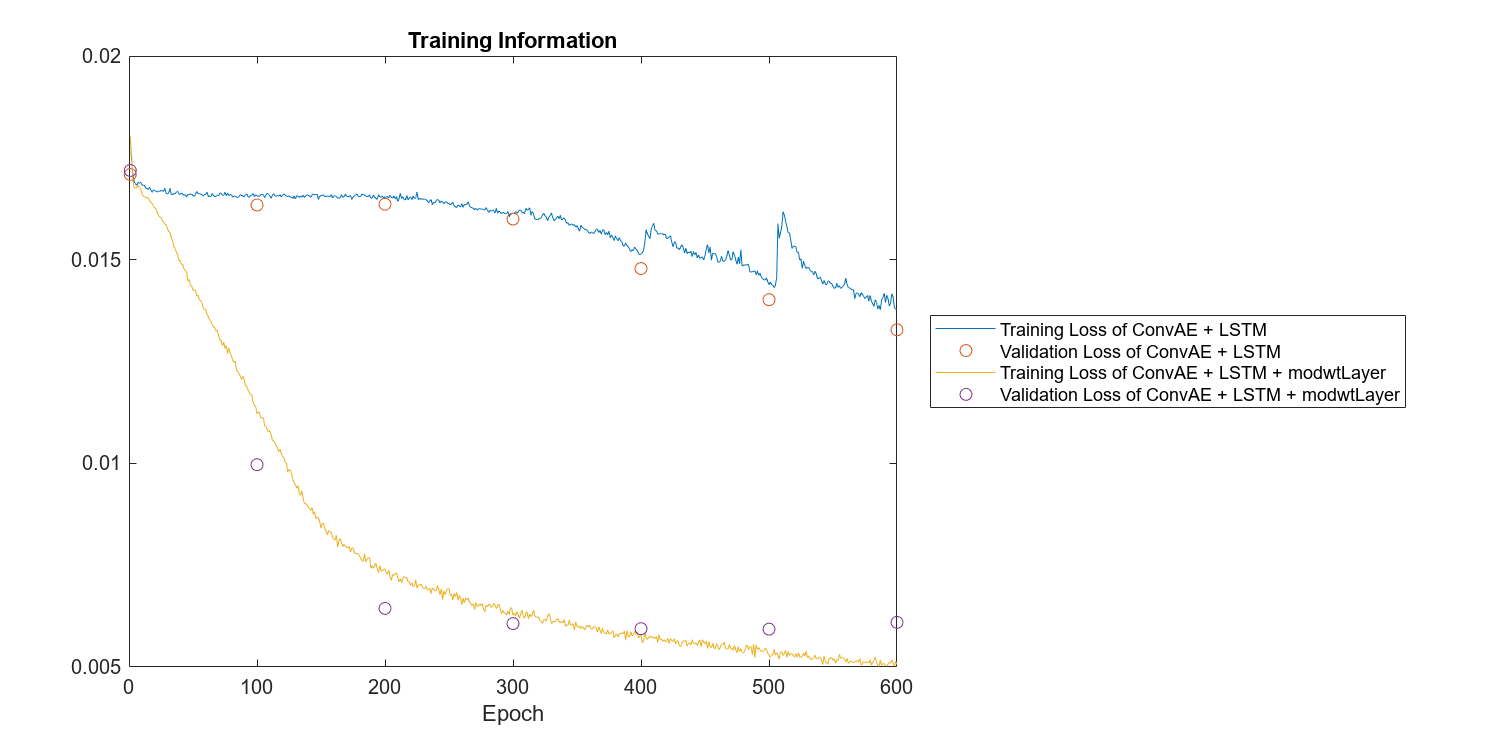
Compare the training and validation losses of two models. Both the training loss and validation loss of the model with MODWT layer drop much faster and more smoothly.
figure plot(info1.TrainingHistory,"Iteration","Loss") hold on scatter(info1.ValidationHistory,"Iteration","Loss") plot(info2.TrainingHistory,"Iteration","Loss") scatter(info2.ValidationHistory,"Iteration","Loss") hold off legend(["Training Loss of ConvAE + LSTM", ... "Validation Loss of ConvAE + LSTM", ... "Training Loss of ConvAE + LSTM + modwtLayer",... "Validation Loss of ConvAE + LSTM + modwtLayer"],"Location","eastoutside") xlabel("Epoch") grid on title("Training Information") set(gcf,'Position',[0 0 1000,500]);
Further compare the reconstructed signals on the same test data samples. The model with modwtLayer can capture the peak position, magnitude, and shape of ECG signals very well in resting and valsalva scenarios. Even in apnea scenarios, with relatively few training samples, it can still capture the main peaks and get reconstructed signals.
helperPlotData(testDs,testindices,net1,net2)
Compare the distributions of the reconstructed signal errors for the two models on the full test set. It further illustrates that using MODWT layer improves the accuracy of the reconstruction.
ecgTestRe1 = minibatchpredict(net1,testData(:,1),InputDataFormats="CTB"); ecgTestReCell1 = squeeze(mat2cell(ecgTestRe1,1,1024,ones(200,1))); loss1 = cellfun(@mse,ecgTestReCell1,testData(:,2)); ecgTestRe2 = minibatchpredict(net2,testData(:,1),InputDataFormats="CTB"); ecgTestReCell2 = squeeze(mat2cell(ecgTestRe2,1,1024,ones(200,1))); loss2 = cellfun(@mse,ecgTestReCell2,testData(:,2)); figure h1 = histogram(loss1); hold on h2 = histogram(loss2); hold off h1.Normalization = 'probability'; h1.BinWidth = 0.003; h2.Normalization = 'probability'; h2.BinWidth = 0.003; ylabel("Probability") xlabel("MSE between Measured and Reconstructed ECG Signals") title("Distribution of Test MSEs") legend(["Model without modwtLayer","Model with modwtLayer"])
Conclusion
This example implements a convolutional autoencoder and BiLSTM network to reconstruct ECG signals from CW radar signals. The example analyzes the performance of the model with and without a MODWT Layer. It shows that the introduction of MODWT layer improves the quality of the reconstructed ECG signals.
Reference
[1] Schellenberger, S., Shi, K., Steigleder, T. et al. A dataset of clinically recorded radar vital signs with synchronised reference sensor signals. Sci Data 7, 291 (2020). https://doi.org/10.1038/s41597-020-00629-5
Appendix — Helper Functions
helperNormalize - this function normalizes input signals by subtracting the median and dividing by the maximum value.
function x = helperNormalize(x) % This function is only intended to support this example. It may be changed % or removed in a future release. x = x-median(x); x = {x/max(x)}; end
helperPlotData - this function plots radar and ECG signals.
function helperPlotData(DS,Indices,net1,net2) % This function is only intended to support this example. It may be changed % or removed in a future release. arguments DS Indices net1 =[] net2 = [] end fs = 200; N = numel(Indices); M = 2; if ~isempty(net1) M = M + 1; end if ~isempty(net2) M = M + 1; end tiledlayout(M, N, 'Padding', 'none', 'TileSpacing', 'compact'); for i = 1:N idx = Indices(i); ds = subset(DS,idx); [~,name,~] = fileparts(ds.UnderlyingDatastores{1}.Files{1}); data = read(ds); radar = data{1}; ecg = data{2}; t = linspace(0,length(radar)/fs,length(radar)); nexttile(i) plot(t,radar) title(["Sample",regexprep(name, {'_','radar'}, '')]) xlabel(["Radar Signal","Time (s)"]) grid on nexttile(N+i) plot(t,ecg) xlabel(["Measured ECG Signal","Time (s)"]) ylim([-0.3,1]) grid on if ~isempty(net1) nexttile(2*N+i) y = minibatchpredict(net1,radar,InputDataFormats="CTB"); plot(t,y) grid on ylim([-0.3,1]) xlabel(["Reconstructed ECG Signal","Time (s)"]) end if ~isempty(net2) nexttile(3*N+i) y = minibatchpredict(net2,radar,InputDataFormats="CTB"); hold on plot(t,y) hold off grid on ylim([-0.3,1]) xlabel(["Reconstructed ECG Signal", "with modwtLayer","Time (s)"]) end end set(gcf,'Position',[0 0 300*N,150*M]) end
See Also
Objects
Functions
You can also select a web site from the following list
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)
Asia Pacific
- Australia (English)
- India (English)
- New Zealand (English)
- 中国
- 日本Japanese (日本語)
- 한국Korean (한국어)