Modal Analysis of a Flexible Flying Wing Aircraft
This example shows computation of bending modes of a flexible wing aircraft. The vibration response of the wing is collected at multiple points along its span. The data is used to identify a dynamic model of the system. The modal parameters are extracted from the identified model. The modal parameter data is combined with the sensor position information to visualize the various bending modes of the wing. This example requires Signal Processing Toolbox™.
The Flexible Wing Aircraft
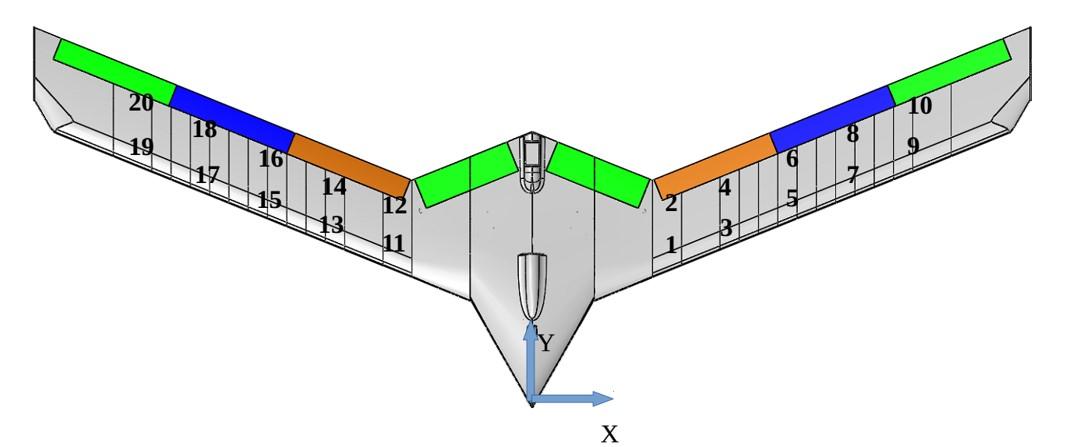
In this example, we study the data gathered from a small flexible flying wing aircraft built at the Uninhabited Aerial Vehicle Laboratories, University of Minnesota [1]. The geometry of the aircraft is shown below.

The aircraft wing can undergo large deformations under loading. The flexible mode frequencies are lower than those in common aircraft with more rigid wings. This flexible design reduces material costs, increases agility and the flight range of the aircraft. However, if not controlled, the flexible modes can lead to catastrophic aeroelastic instabilities (flutter). Designing effective control laws for suppressing these instabilities requires accurate determination of the wing's various bending modes.
Experimental Setup
The objective of the experiment is to gather vibration response of the aircraft at various locations in response to an external excitation. The aircraft is suspended from a wooden frame using a single spring at its center of gravity. The spring is sufficiently flexible so that the natural frequency of the spring-mass oscillation does not interfere with the fundamental frequencies of the aircraft. An input force is applied via an Unholtz-Dickie Model 20 electrodynamic shaker near the center of the aircraft.


Twenty PCB-353B16 accelerometers are placed along the wing span to collect the vibration response as shown in the next figure.
The shaker input command is specified as a constant amplitude chirp input of the form . The chirp frequency varies linearly with time, that is, . The frequency range covered by the input signal is 3–35 Hz. The data is collected by two accelerometers (leading and trailing edge accelerometers at one x-location) at a time. Hence 10 experiments are conducted to collect all the 20 accelerometer responses. The accelerometer and force transducer measurements are all sampled at 2000 Hz.
Data Preparation
The data is represented by 10 sets of two-output/one-input signals, each containing 600K samples. The data is available at the MathWorks support files site. See the disclaimer. Download the data file and load the data into the MATLAB® workspace.
url = 'https://www.mathworks.com/supportfiles/ident/flexible-wing-GVT-data/FlexibleWingData.mat'; websave('FlexibleWingData.mat',url); load FlexibleWingData.mat MeasuredData
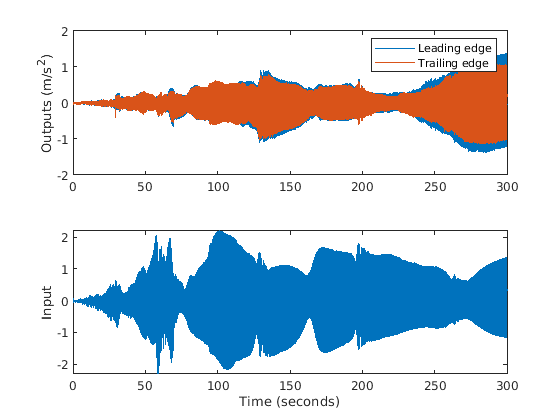
The variable MeasuredData is a structure with fields Exp1, Exp2, ..., Exp10. Each field is a structure with fields y and u containing the two responses and the corresponding input force data. Plot the data for the first experiment.
fs = 2000; % data sampling frequency Ts = 1/fs; % sample time y = MeasuredData.Exp1.y; % output data (2 columns, one for each accelerometer) u = MeasuredData.Exp1.u; % input force data t = (0:length(u)-1)' * Ts; figure subplot(211) plot(t,y) ylabel('Outputs (m/s^2)') legend('Leading edge','Trailing edge') subplot(212) plot(t,u) ylabel('Input') xlabel('Time (seconds)')
In order to prepare data for model identification, the data is packaged into iddata objects. The iddata objects are standard way of packaging time-domain data in System Identification Toolbox™. The input signal is treated as bandlimited.
ExpNames = fieldnames(MeasuredData); Data = cell(1, 10); for k = 1:10 y = MeasuredData.(ExpNames{k}).y; u = MeasuredData.(ExpNames{k}).u; Data{k} = iddata(y, u, Ts, 'InterSample', 'bl'); end
Merge the dataset objects into one multi-experiment data object.
Data = merge(Data{:})Data =
Time domain data set containing 10 experiments.
Experiment Samples Sample Time
Exp1 600001 0.0005
Exp2 600001 0.0005
Exp3 600001 0.0005
Exp4 600001 0.0005
Exp5 600001 0.0005
Exp6 600001 0.0005
Exp7 600001 0.0005
Exp8 600001 0.0005
Exp9 600001 0.0005
Exp10 600001 0.0005
Outputs Unit (if specified)
y1
y2
Inputs Unit (if specified)
u1
Model Identification
We want to identify a dynamic model whose frequency response matches that of the actual aircraft as closely as possible. A dynamic model encapsulates a mathematical relationship between the inputs and outputs of the system as a differential or difference equation. Examples of dynamic models are transfer functions and state-space models. In System Identification Toolbox, dynamic models are encapsulated by objects such as idtf (for transfer functions), idpoly (for AR, ARMA models) and idss (for state-space models). Dynamic models can be created by running estimation commands such as tfest and ssest commands on measured data in either time-domain or frequency-domain.
For this example, we first convert the measured time-domain data into frequency response data by empirical transfer function estimation using the etfe command. The estimated FRF is then used to identify a state-space model of the aircraft's vibration response. It is possible to directly use time-domain data for dynamic model identification. However, FRF form of data allows compression of large datasets into fewer samples as well as more easily adjust estimation behavior to relevant frequency ranges. FRFs are encapsulated by idfrd objects.
Estimate a two-output/one-input frequency response function (FRF) for each data experiment. Use no windowing. Use 24,000 frequency points for response computation.
G = cell(1, 10); N = 24000; for k = 1:10 % Convert time-domain data into a FRF using ETFE command Data_k = getexp(Data, k); G{k} = etfe(Data_k, [], N); % G{k} is an @idfrd object end
Concatenate all FRFs into a single 20-output/one-input FRF.
G = cat(1, G{:}); % concatenate outputs of all estimated FRFs
G.OutputName = 'y'; % name outputs 'y1', 'y2', ..., 'y20'
G.InterSample = 'bl';To get a feel for the estimated frequency response, plot the amplitude for outputs 1 and 15 (picked arbitrarily). Zoom into the frequency range of interest (4–35 Hz).
opt = bodeoptions; % plot options opt.FreqUnits = 'Hz'; % show frequency in Hz opt.PhaseVisible = 'off'; % do not show phase OutputNum = [1 15]; % pick outputs 1 and 15 for plotting clf bodeplot(G(OutputNum, :), opt) % plot frequency response xlim([4 35]) grid on
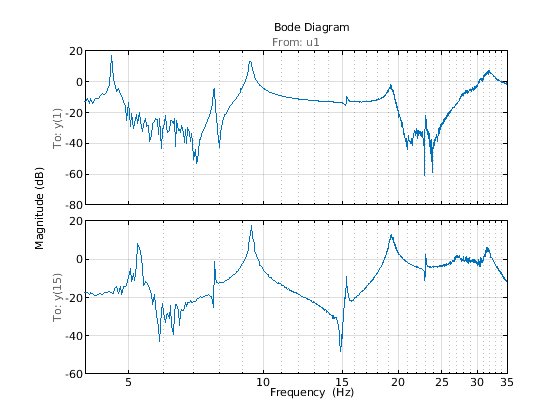
The FRF shows at least 9 resonant frequencies. For analysis we want to focus on 6-35 Hz frequency span where the most critical flexible bending modes of the aircraft lie. Hence reduce the FRF to this frequency region.
f = G.Frequency/2/pi; % extract frequency vector in Hz (G stores frequency in rad/s) Gs = fselect(G, f>6 & f<=32) % "fselect" selects the FRF in the requested range (6.5 - 35 Hz)
Gs = IDFRD model. Contains Frequency Response Data for 20 output(s) and 1 input(s). Response data is available at 624 frequency points, ranging from 37.96 rad/s to 201.1 rad/s. Sample time: 0.0005 seconds Output channels: 'y(1)', 'y(2)', 'y(3)', 'y(4)', 'y(5)', 'y(6)', 'y(7)', 'y(8)', 'y(9)', 'y(10)', 'y(11)', 'y(12)', 'y(13)', 'y(14)', 'y(15)', 'y(16)', 'y(17)', 'y(18)', 'y(19)', 'y(20)' Input channels: 'u1' Status: Estimated model
Gs thus contains the frequency response measurements at the 20 measurement locations. Next, identify a state-space model to fit Gs. The subspace estimator n4sid provides a quick noniterative estimate. The state-space model structure is configured as follows:
We estimate an 24th-order continuous-time model. The order was found after some trials with various orders and checking the resulting fit of the model to the FRF.
The model contains a feedthrough term (D matrix is non-zero). This is because we are limiting our analysis to 35 Hz while the wing's bandwidth is significantly larger than that (response is significant at 35 Hz).
To speed up computation, we suppress computation of parameter covariance.
The FRF magnitude varies significantly across the frequency range. In order to ensure that the low amplitudes receive equal emphasis as the higher amplitudes, we apply a custom weighting that varies inversely as the square root of the response. Since there are 20 channels, the weighting vector is taken as the mean of the weights obtained from each (this works because the FRFs of the 20 channels are similar in shape).
We set up the estimation options for n4sid using n4sidOptions.
FRF = squeeze(Gs.ResponseData); Weighting = mean(1./sqrt(abs(FRF))).'; n4Opt = n4sidOptions('EstimateCovariance',false,... 'WeightingFilter',Weighting,... 'OutputWeight',eye(20)); sys1 = n4sid(Gs,24,'Ts',0,'Feedthrough',true,n4Opt); Fit = sys1.Report.Fit.FitPercent'
Fit = 1×20
54.2689 55.3738 84.0188 85.7017 81.9259 80.2293 55.7448 40.6773 58.6429 76.2997 83.5370 84.6555 85.9240 84.8780 76.8937 81.0399 74.8321 79.4069 65.0803 76.3328
The "Fit" numbers shows the percentage fit between the data (Gs) and model's (sys1) frequency response using a normalized root-mean-square-error (NRMSE) goodness-of-fit measure. The poorest and best fits are plotted next.
[~,Imin] = min(Fit); [~,Imax] = max(Fit); clf bodeplot(Gs([Imin, Imax],:), sys1([Imin, Imax],:), opt); xlim([6 32]) title('Worst (top) and best (bottom) fits between data and model') grid on legend('Data', 'Model')

The fits achieved with model sys1 can be improved even more by iterative nonlinear least-squares refinement of model's parameters. This can be achieved using the ssest command. We set up the estimation options for ssest using the ssestOptions command. This time the parameter covariance is also estimated.
ssOpt = ssestOptions('EstimateCovariance',true,... 'WeightingFilter',n4Opt.WeightingFilter,... 'SearchMethod','lm',... % use Levenberg-Marquardt search method 'Display','on',... 'OutputWeight',eye(20)); sys2 = ssest(Gs, sys1, ssOpt); % estimate state-space model (this takes several minutes) Fit = sys2.Report.Fit.FitPercent'
Fit = 1×20
88.8715 88.6587 88.9388 89.8630 87.8597 88.1235 79.7016 82.5930 74.2458 82.6593 90.2663 88.7739 89.9033 89.0571 88.8040 88.2251 86.9307 87.5250 83.2249 82.8676
As before we plot the worst and the best fits. We also visualize the 1-sd confidence region for the model's frequency response.
[~, Imin] = min(Fit); [~, Imax] = max(Fit); clf h = bodeplot(Gs([Imin, Imax],:), sys2([Imin, Imax],:), opt); showConfidence(h, 1) xlim([6.5 35]) title('Worst (top) and best (bottom) fits between data and refined model') grid on legend('Data', 'Model (sys2)')
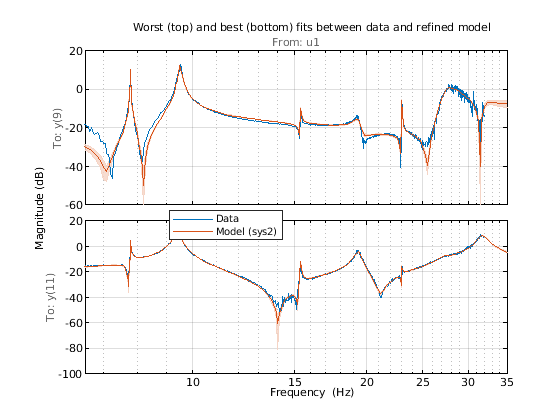
The refined state-space model sys2 fits the FRFs quite well in the 7–20 Hz region. The uncertainty bounds are tight around most resonant locations. We estimated a 24th-order model which means that there are at most 12 oscillatory modes in the system sys2. Use the modalfit command to fetch the natural frequencies in Hz for these modes.
f = Gs.Frequency/2/pi; % data frequencies (Hz) fn = modalfit(sys2, f, 12); % natural frequencies (Hz) disp(fn)
7.7720
7.7954
9.3176
9.4052
9.4919
15.3462
19.3281
23.0219
27.4035
28.6873
31.7036
64.2624
The values in fn suggest two frequencies very close to 7.8 Hz and three close to 9.4 Hz. An inspection of frequency responses near these frequencies reveals that the peaks location shift a little bit across outputs. These discrepancies may be removed by better control over the experiment process, performing direct time-domain identification with input bandwidth limited to narrow range centered at these frequencies, or fitting a single oscillatory mode to the frequency response around these frequencies. These alternatives are not explored in this example.
Modal Parameter Computation
We can now use the model sys2 to extract the modal parameters. An inspection of the FRFs indicates around 10 modal frequencies, roughly around the frequencies [5 7 10 15 17 23 27 30] Hz. We can make this assessment more concrete by using the modalsd command that checks the stability of modal parameters as the order of the underlying model is changed. This operation takes a long time. Hence the resulting plot is inserted directly as an image. Execute the code inside the comment block below to reproduce the figure.
FRF = permute(Gs.ResponseData,[3 1 2]); f = Gs.Frequency/2/pi; %{ figure pf = modalsd(FRF,f,fs,'MaxModes',20,'FitMethod','lsrf'); %}
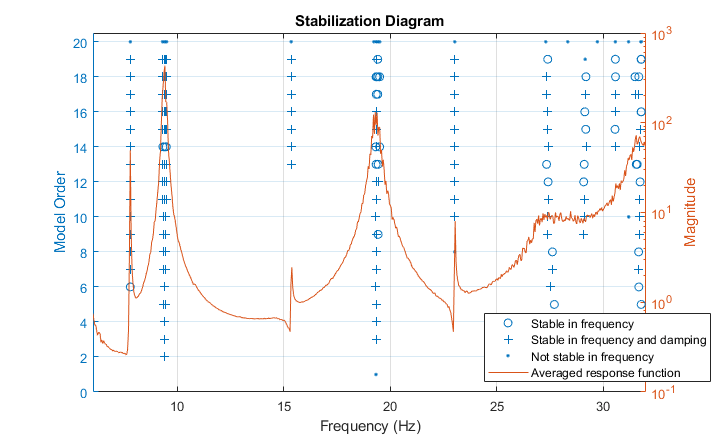
Inspection of the plot and pf values suggests a refined list of true natural frequencies:
Freq = [7.8 9.4 15.3 19.3 23.0 27.3 29.2 31.7];
We use the values in Freq vector as a guide for picking most dominant modes from the model sys2. This is done using the modalfit command.
[fn,dr,ms] = modalfit(sys2,f,length(Freq),'PhysFreq',Freq);fn are the natural frequencies (in Hz), dr the corresponding damping coefficients and ms the normalized residuals as column vectors (one column for each natural frequency). In the process of extraction of these modal parameters, only the stable, under-damped poles of the model are used. The ms columns contain data for only the poles with positive imaginary part.
Mode Shape Visualization
To visualize the various bending modes, we need the modal parameters extracted above. In addition we need information on the location of the measurement points. These positions (x-y values) is recorded for each accelerometer in the matrix AccePos:
AccelPos = [... % see figure 2 16.63 18.48; % nearest right of center 16.63 24.48; 27.90 22.22; 27.90 28.22; 37.17 25.97; 37.17 31.97; 46.44 29.71; 46.44 35.71; 55.71 33.46; 55.71 39.46; % farthest right -16.63 18.48; % nearest left of center -16.63 24.18; -27.90 22.22; -27.90 28.22; -37.17 25.97; -37.17 31.97; -46.44 29.71; -46.44 35.71; -55.71 33.46; -55.71 39.46]; % farthest left
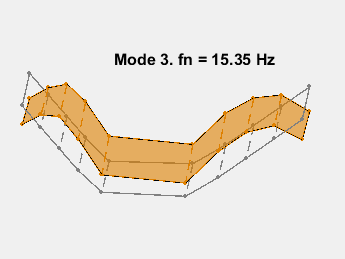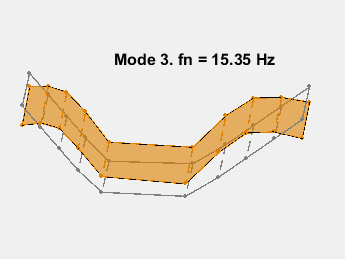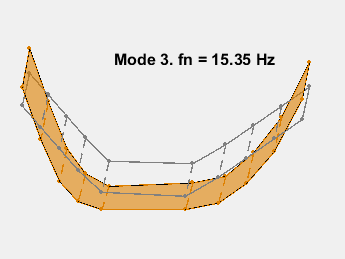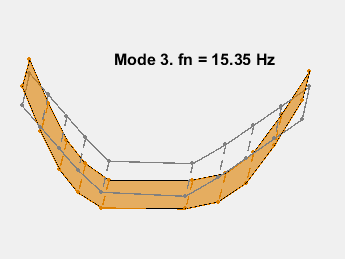
The mode shapes are contained in the matrix ms where each column corresponds to the shape for one frequency. Animate the mode by superimposing mode shape amplitudes over the sensor coordinates and varying the amplitudes at the mode's natural frequency. The animation shows the bending with no damping. As an example, consider the mode at 15.3 Hz.
AnimateOneMode(3, fn, ms, AccelPos);
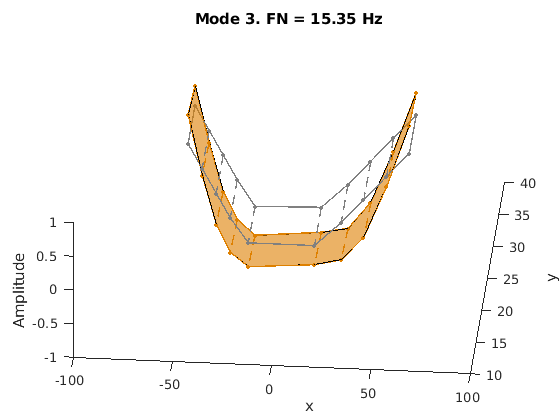
Conclusions
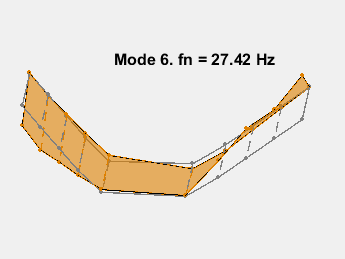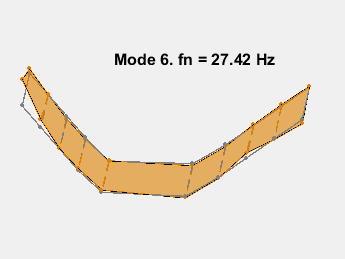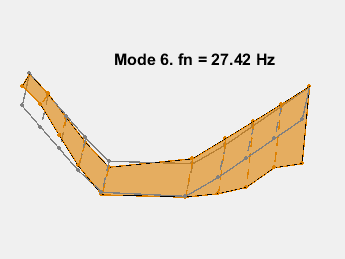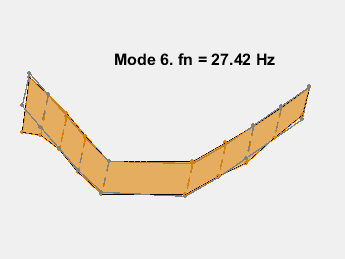
This example shows a parametric model identification based approach to modal parameter estimation. Using a state-space model of 24th order, 8 stable oscillatory modes in the frequency region 6–32 Hz were extracted. The modal information was combined with the knowledge of the accelerometer positions to visualize the various bending modes. Some of these modes are shown in the figures below.


References
[1] Gupta, Abhineet, Peter J. Seiler, and Brian P. Danowsky. "Ground Vibration Tests on a Flexible Flying Wing Aircraft." AIAA Atmospheric Flight Mechanics Conference, AIAA SciTech Forum. (AIAA 2016-1753).
function AnimateOneMode(ModeNum, fn, ModeShapes, AccelPos) % Animate one mode. % ModeNum: Index of the mode. % Reorder the sensor locations for plotting so that a continuous, % non-intersecting curve is traced around the body of the aircraft. PlotOrder = [19:-2:11, 1:2:9, 10:-2:2, 12:2:20, 19]; Fwd = PlotOrder(1:10); Aft = PlotOrder(20:-1:11); x = AccelPos(PlotOrder,1); y = AccelPos(PlotOrder,2); xAft = AccelPos(Aft,1); yAft = AccelPos(Aft,2); xFwd = AccelPos(Fwd,1); yFwd = AccelPos(Fwd,2); wn = fn(ModeNum)*2*pi; % Mode frequency in rad/sec T = 1/fn(ModeNum); % Period of modal oscillation Np = 2.25; % Number of periods to simulate tmax = Np*T; % Simulate Np periods Nt = 100; % Number of time steps for animation t = linspace(0,tmax,Nt); ThisMode = ModeShapes(:,ModeNum)/max(abs(ModeShapes(:,ModeNum))); % normalized for plotting z0 = ThisMode(PlotOrder); zFwd = ThisMode(Fwd); zAft = ThisMode(Aft); clf col1 = [1 1 1]*0.5; xx = reshape([[xAft, xFwd]'; NaN(2,10)],[2 20]); yy = reshape([[yAft, yFwd]'; NaN(2,10)],[2 20]); plot3(x,y,0*z0,'-', x,y,0*z0,'.', xx(:), yy(:), zeros(40,1),'--',... 'Color',col1,'LineWidth',1,'MarkerSize',10,'MarkerEdgeColor',col1); xlabel('x') ylabel('y') zlabel('Amplitude') ht = max(abs(z0)); axis([-100 100 10 40 -ht ht]) view(5,55) title(sprintf('Mode %d. FN = %s Hz', ModeNum, num2str(fn(ModeNum),4))); % Animate by updating z-coordinates. hold on col2 = [0.87 0.5 0]; h1 = plot3(x,y,0*z0,'-', x,y,0*z0,'.', xx(:), yy(:), zeros(40,1),'--',... 'Color',col2,'LineWidth',1,'MarkerSize',10,'MarkerEdgeColor',col2); h2 = fill3(x,y,0*z0,col2,'FaceAlpha',0.6); hold off for k = 1:Nt Rot1 = cos(wn*t(k)); Rot2 = sin(wn*t(k)); z_t = real(z0)*Rot1 - imag(z0)*Rot2; zAft_t = real(zAft)*Rot1 - imag(zAft)*Rot2; zFwd_t = real(zFwd)*Rot1 - imag(zFwd)*Rot2; zz = reshape([[zAft_t, zFwd_t]'; NaN(2,10)],[2 20]); set(h1(1),'ZData',z_t) set(h1(2),'ZData',z_t) set(h1(3),'ZData',zz(:)) h2.Vertices(:,3) = z_t; pause(0.1) end end
