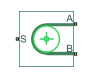
Belt Pulley
Power transmission element with frictional belt wrapped around pulley circumference
Libraries:
Simscape /
Driveline /
Couplings & Drives
Description
The Belt Pulley block represents a pulley wrapped in a
flexible ideal, flat, or V-shaped belt. When you set Belt type to
Ideal - No slip, the belt does not slip relative to the
pulley surfaces. You can optionally enable pulley linear translation.
The block accounts for friction between the flexible belt and the pulley surface. The tensioner slips when the load exceeds the friction force. The block accounts for centrifugal loading in the flexible belt, pulley inertia, and bearing friction.

The belt ends can either move in the same direction or in the opposite direction.
The block equations relate power transmission between the belt branches or to or from the pulley. The driving and driven branches use the same calculation. Without sufficient tension, the frictional force is not enough to transmit power between the pulley and belt.
Your model is valid when both ends of the belt are in tension. You can choose to display a warning in the Simulink® Diagnostic Viewer when the leading belt end loses tension. When assembling a model, ensure that tension is maintained throughout the simulation by adding mass to at least one of the belt ends or by adding a tensioner like the Cable block. Use the Variable Viewer to ensure that any springs attached to the belt are in tension. For more details on building a tensioner, see Best Practices for Modeling Pulley Networks.
You can set Friction model to Modal to use a
modal parameterization for the pulley. Choose the modal parameterization for greater
numerical robustness. To enable this parameter, clear the Pulley
translation parameter.
The Belt Pulley block uses a composite implementation of the Fundamental Friction Clutch block to produce the conditions for the modal parameterization.
Equations
For either setting of the Friction model parameter, the block equations refer to these quantities:
β is the belt direction sign. When you set Belt direction to
Ends move in same direction, β = 1. Otherwise, β = -1.Vrel is the relative velocity between the belt and pulley periphery. Vrel = 0 when Belt type is
Ideal - No slip.VA is the linear velocity of branch A.
VB is the linear velocity of branch B.
VC is the linear velocity of the pulley at its center. When you clear Pulley translation, the block constrains this value to 0.
ωS is the angular velocity of the pulley contact surface.
R is the radius of the pulley.
Fcentrifugal is centrifugal force of the belt.
FC is the force acting through the pulley centroid. When you specify a value for Inertia, FC includes force due to the pulley mass acceleration.
ρ is the belt linear density.
Ffr is the friction force between the pulley and the belt.
FA is the force acting along branch A.
FB is the force acting along branch B.
θ is the contact wrap angle.
τS is the pulley torque.
The kinematic constraints between the pulley and belt are:
When you set Belt type to either V-belt or
Flat belt and set Centrifugal
force to Model centrifugal force, the
centrifugal force is:
When you select Pulley translation, the force balancing equation is:
To calculate Fcentrifugal,smooth,sat, the block
Smooths Fcentrifugal using Fthr. You can increase smoothing by raising Fthr, and you can decrease smoothing by lowering Fthr.
Saturates values above βFA-FB.

The sign convention is such that, when Belt direction is
Ends move in opposite direction, a positive rotation
in port S results in a negative translation for port
A and a positive translation for port
B.
To enable the Friction model parameter, set Belt
type to Flat belt or
V-belt and clear Pulley
translation.
When you set Friction model to Continuous,
the block equations refer to these quantities:
μ is the Contact friction coefficient parameter.
μsmoothed is the instantaneous value of the friction coefficient.
Vthr is the Velocity threshold parameter.
b is the viscous damping of the bearing.
Fthr is the Force threshold parameter.
The instantaneous friction coefficient is a function of the relative velocity such that
where the hyperbolic tangent function maintains numerical robustness by ensuring a smooth and continuous output for Vrel zero-crossings.
For a V-belt, the block derives the contact friction value using the sheave angle:
where:
μsheave is the effective friction coefficient.
Φ is the sheave angle.
For a flat belt, μsheave = μ.
The friction velocity threshold controls the width of the region within which the friction
coefficient changes its value from zero to a steady-state maximum. The friction
velocity threshold specifies the velocity at which the hyperbolic tangent equals
0.999. The smaller the value, the steeper the change of
μ.
The block determines the effect of friction on the force at the belt ends as:
which follows the form of the capstan equation, also known as the Euler-Eytelwein equation. The torque acting on the pulley is
where σ = 1 when you set Belt type to
Ideal - No slip. Otherwise,
For a V-belt, the block derives the static and kinetic friction values by using the sheave angle:
where:
μStatic is the Static friction coefficient parameter.
μStatic,sheave is effective static friction coefficient.
μKinetic is the Kinetic friction coefficient parameter.
μKinetic,sheave is effective kinetic friction coefficient.
Φ is the sheave angle.
For a flat belt, μStatic,sheave = μStatic, and μKinetic,sheave = μKinetic.
When you set Friction model to
Modal, the block calculates the maximum static
friction force before slipping as
where FFriction,Static,Max is the maximum force magnitude due to static friction, and FDrive is the force due to tension felt at the end of the pulley with the greatest force magnitude. As with Fcentrifugal, the block uses Fthr to smooth FDrive. To increase or decrease the smoothing on FDrive, raise of lower the value of the Force threshold parameter.
The block smoothly saturates FFriction,Static,Max to be greater than or equal to 0 as
During slip,
where μKinetic,sheave is the kinetic friction coefficient. The block resolves the torque balance using
and
where Simscape™ logs RFFriction as
fundamental_clutch.torque.
Examples
Assumptions and Limitations
The block assumes noncompliance along the length of the belt.
The block assumes both belt ends maintain adequate tension throughout the simulation.
The block treats the translation of the pulley center as planar where the pulley travels along the bisect of the pulley wrap angle. The center velocity VC and force FC only account for the component along this line of motion.
The Eytelwein equation for belt friction neglects the effect of pulley translation on friction.
Ports
Conserving
Parameters
More About
References
[1] Johnson, Kenneth L. Contact Mechanics. Cambridge: Cambridge Univ. Press, 2003.